三角形と垂線

この著者は初心者として投稿しています。間違いや考慮が足りていない点が含まれている可能性が高いです。見つけたらコメント欄で優しく指摘してあげましょう。

はじめに

三角形のある頂点から対辺に垂らした垂線について、
垂線の足が対辺を分割するときの比について考察した。

下図について次の等式が成立する。
$$ c_\mathrm{A}:c_\mathrm{B}=(c^2+b^2-a^2):(c^2+a^2-b^2)$$

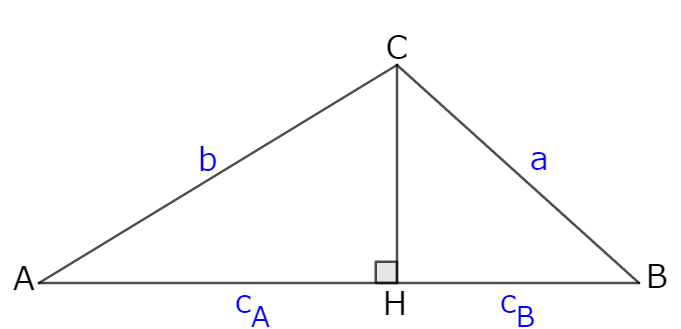
とくに$\angle \mathrm{C}=\frac{\pi}{2}$のとき$c^2=a^2+b^2$なので
$$c_\mathrm{A}:c_\mathrm{B}=b^2:a^2 $$

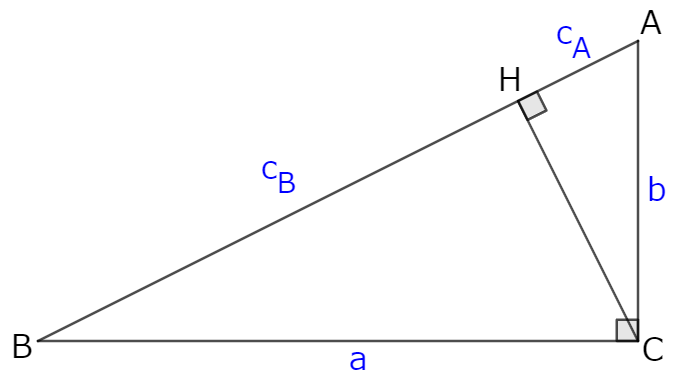
三平方の定理より
$$c_\mathrm{A}^2+\mathrm{CH}^2=b^2$$
$$c_\mathrm{B}^2+\mathrm{CH}^2=a^2$$
辺々引くと
$$c_\mathrm{A}^2-c_\mathrm{B}^2=b^2-a^2$$
変形して
$$(c_\mathrm{A}+c_\mathrm{B})(c_\mathrm{A}-c_\mathrm{B})=b^2-a^2$$
ここで
$$c_\mathrm{A}+c_\mathrm{B}=c$$
なので、
$$c(c_\mathrm{A}-c_\mathrm{B})=b^2-a^2$$
また、
$$c(c_\mathrm{A}+c_\mathrm{B})=c^2$$
なので
$P=c(c_\mathrm{A}+c_\mathrm{B})$、$Q=c(c_A-c_B)$とおくと
$$\frac{c_\mathrm{B}}{c_\mathrm{A}}=\frac{P-Q}{P+Q}=\frac{c^2-(b^2-a^2)}{c^2+(b^2-a^2)}$$

投稿日：3月7日

更新日：3月7日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

バッチを贈って投稿者を応援しよう

バッチを贈ると投稿者に現金やAmazonのギフトカードが還元されます。

投稿者

tanu

21321

他の人のコメント

コメントはありません。

読み込み中

tanu

三角形と垂線