0の0乗について

はじめに

0の0乗について考えてみます。
厳密な論理展開は苦手なので、実験と推測によって議論を進めました。

結論としては、

$0^0$は定義されない。
考え方によっては、$0$、$1$、$\infty$をこじつけることが可能だが、
他の計算結果との整合性（連続性）を重視すると$1$が有望

みたいな感じになりました。

方針

3種類の関数$f(x)=x^x$、$g(x)=a^x$、$h(x)=x^a$について、極限などをみてみる

$f(x)=x^x$

関数$f(x)=x^x$のグラフはこんな感じ

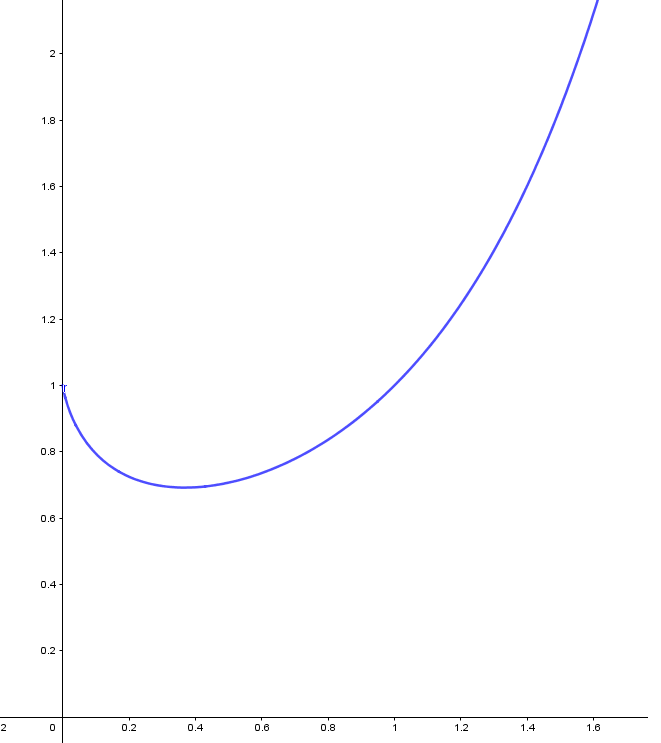
よって見た感じ
$$ \lim_{x \to +0}x^x=1$$

$g(x)=a^x$

$a=10^{-4}$のときのグラフがこんな感じ
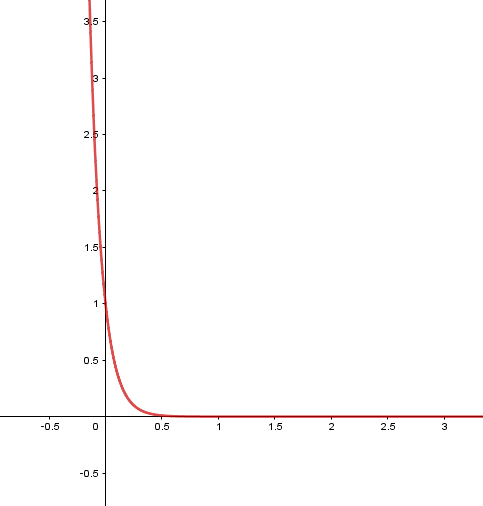
この感じだと、$a \to +0$としても
$$\lim_{x \to -0}g(x)=\lim_{x \to +0}g(x)=g(0)=1$$
が成立すると考えて良さそう。

$h(x)=x^a$

$a=0$のとき

グラフはこんな感じ。　※h(0)は保留

このとき
$$\lim_{x \to -0}h(x)=\lim_{x \to +0}h(x)=1$$

$a \to +0$のとき

$a$に小さい正数を入れてグラフを観察した結果から推測すると
グラフはこんな感じになる。

このとき
$$\lim_{x \to +0}h(x)=1$$
$$h(0)=0$$

$a \to -0$のとき

$a$に小さい負数を入れてグラフを観察した結果から推測すると
グラフはこんな感じになる。

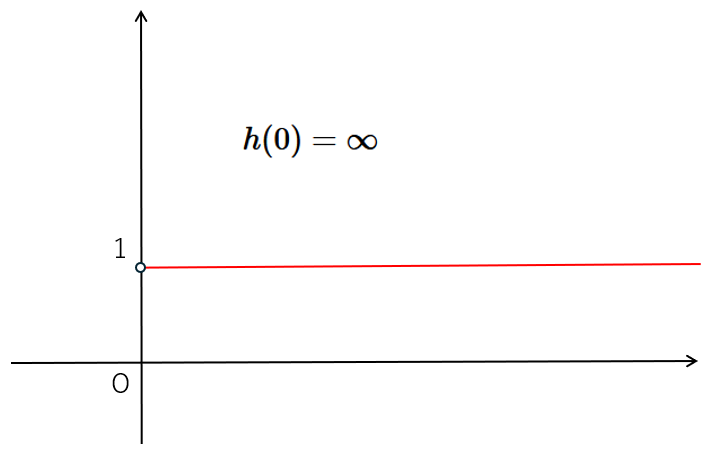
このとき
$$\lim_{x \to +0}h(x)=1$$
$$h(0)=\infty$$

おわりに

$0^0=1$と定義してしまいたくなるほどに$1$が優勢な感じでしたが
$x^a$のグラフで、$a$が負のときにグラフが$\infty$にとんでいく様子をみると、とても気持ちが不安定になるので、「定義されない」と結論しました。異論は認めます。