自作問題とその解説
はじめに
こんにちは!中学3年生のUです!
今日は自作問題の解説をしたいと思います.
よろしくお願いします.
問題
$AB$$\lt$$AC$なる鋭角三角形$ABC$の辺$AB$,$AC$と$2$点$B$,$C$を通る円の交点を$D$,$E$とする.$\angle$$BAC$の二等分線と直線$DE$,$BC$の交点を$P$,$Q$とし,線分$BE$と$CD$の交点を$R$とする.また,三角形$DRE$の外接円と三角形$BRC$の外接円の交点を$K$とすると,$\angle$$CBE$$=$$\angle$$PKD$が成り立ちました.直線$PK$と点$C$を通り$DE$に平行な直線との交点を$L$とし,直線$DL$と$BC$の交点を$F$とする.また,辺$AC$上に点$X$を$FX$$=$$FC$を満たすようにとり,直線$RK$と$BC$の交点を$Y$とする.このとき,直線$FX$は三角形$XYQ$の外接円に接することを示せ.
まだ解いていない方はぜひ一度考えてみてください!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
!
解説(適当ですが許してください)
まずは図を描いてみます.
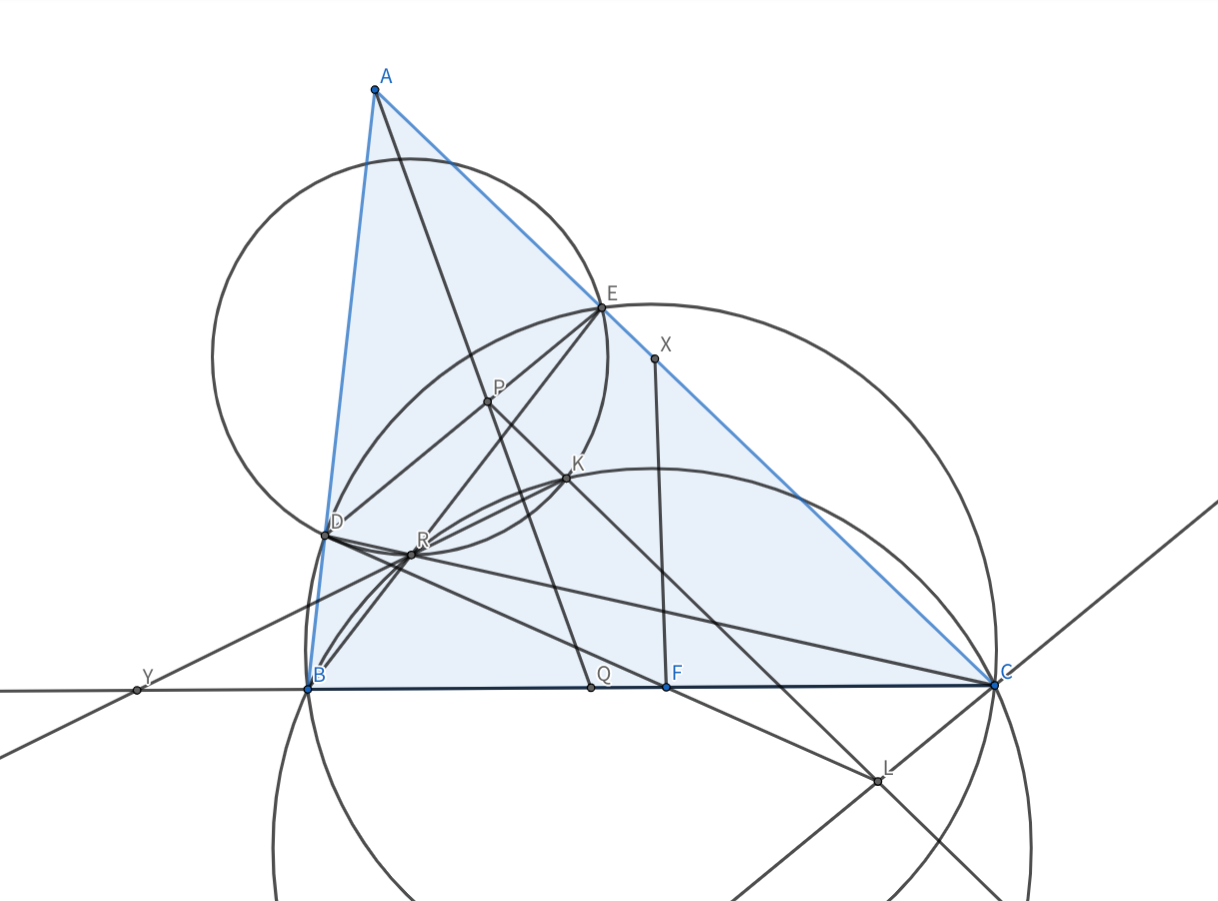
こんな感じですね.
明らかに$Y$は図の3円の根心なので$Y$,$D$,$E$は共線です.$X$をどう扱えばいいのかわかりませんが,とりあえず放置します.また$K$は完全四辺形$BDCE$のミケル点です!!これより$\triangle$$KED$$\sim$$\triangle$$KBC$$←*$が得られますね.
$P$,$Q$の特徴づけをしたいです.内角の二等分線という条件を上手く使いましょう.
$DP$$:$$PE$$=$$AD$$:$$AE$$=$$AC$$:$$AB$$=$$CQ$$:$$QB$なので,*の相似において$P$と$Q$が対応します!よって,$\angle$$DPK$$=$$\angle$$CQK$なので,4点$PYQK$は共円です!!したがって,$DE$$/\!/$$CL$と合わせて$\angle$$QKL$$=$$\angle$$QYP$$=$$\angle$$QCL$であり,$KCLQ$の共円がわかります.ここで問題文の条件$\angle$$CBE$$=$$\angle$$PKD$を使います.$\angle$$CDY$$=$$180$$-$$\angle$$CDE$$=$$180$$-$$\angle$$CBE$$=$$180$$-$$\angle$$PKD$$=$$180$$-$$\angle$$QKC$$=$$\angle$$QLC$です.また,$YD$$/\!/$$CL$より,$\angle$$CYD$$=$$\angle$$QCL$なので$\triangle$$CYD$$\sim$$\triangle$$QCL$です!!
ここで示したいことをもう一度確認します.(少し考えてみるとわかりますが)$angle$ $chase$から接弦定理の逆などを用いて題意を示すのは厳しそうです.$FX$$=$$FC$という条件もありますし,方べきの逆から示せそうです!前述の相似から$CD$$/\!/$$QL$がわかるので$\angle$$CDF$$=$$\angle$$QLF$ですね.よって,点$F$が線分$CY$と線分$QC$を同じ比に内分します.
したがって,$QF$$:$$FC$$=$$CF$$:$$FY$ すなわち $FX^{2}$$=$$FC^{2}$$=$$FQ$$\cdot$$FY$が成り立ちます!解けました!!
さいごに
作問って難しいですね.数オリの作問者の凄さを改めて実感しました.間違っているところなどあれば言ってください〜
読んでくださった方や解いてくださった方,ありがとうございました!