ISL2022G6を解いてみよう．
お久しぶりです．春合宿の問題を漁っていたら計算がブッ刺さるむずめの幾何があったのでご紹介します．
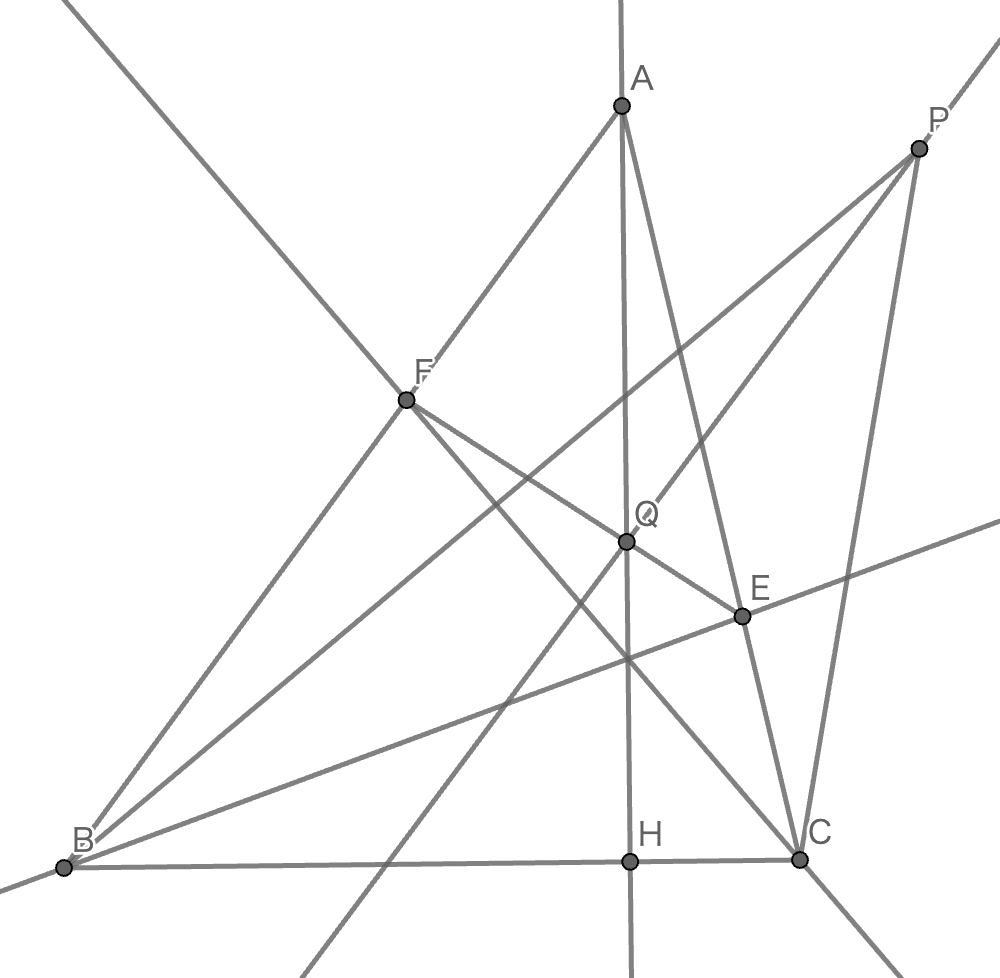
鋭角三角形 $ABC$があり, $A$ から辺 $BC$ に下ろした垂線の足を $H$ とする. 直線 BC 上にない点 $P$ を, $\angle PBC$ の二等分線 k と $\angle PCB$ の二等分線 $l$ が線分 $AH$ 上 (端点を除く) で 交わるようにとる. $k$ と直線 $AC$ の交点を $E$, $l$ と直線 $AB$ の交点を $F$, 直線 $EF$ と直線 $AH$ の交点を $Q$ とする. このとき, ある点 $X$ があり, $P$ のとり方によらず $X$ は直線 $PQ$ 上にある ことを示せ.
画像の名前
まず気づくこと
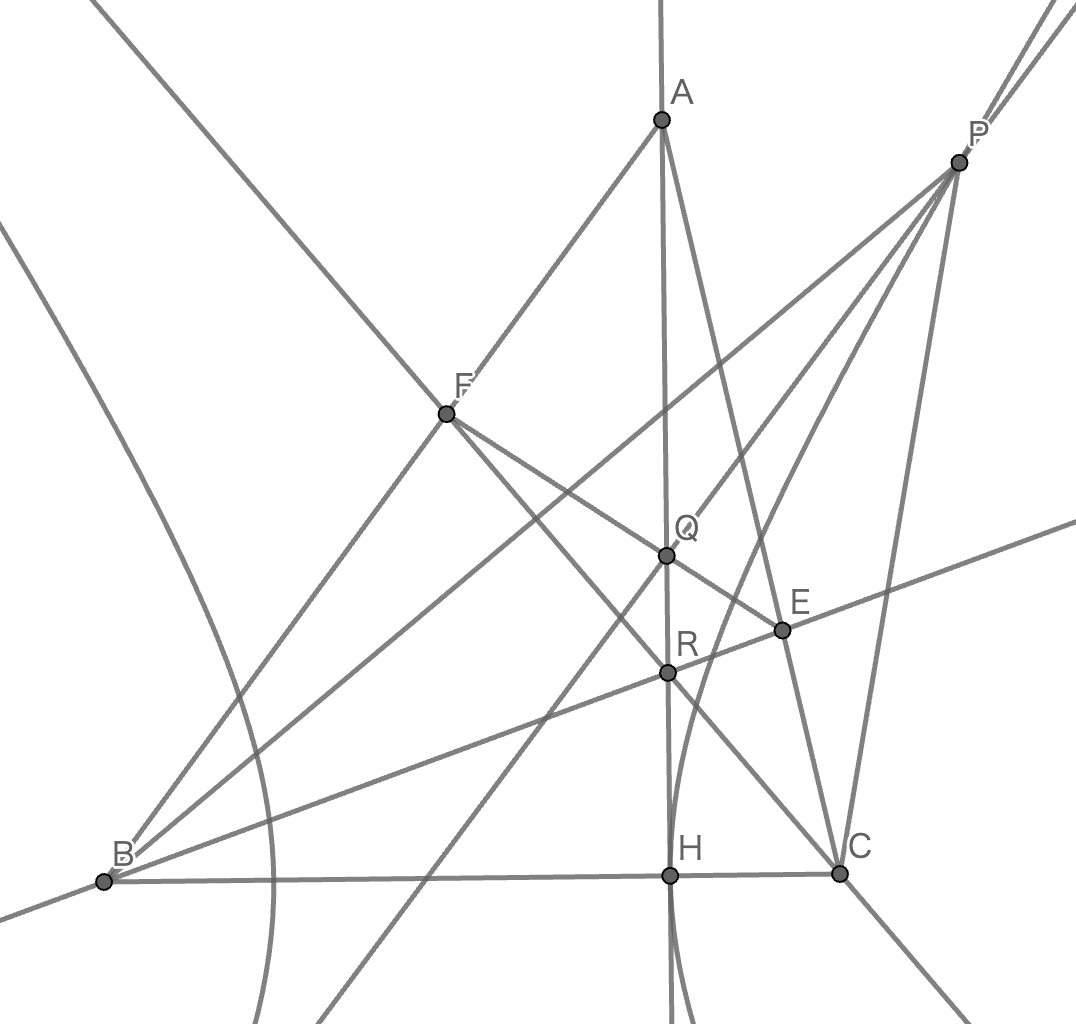
$k,l,AH$の交点を$R$とするとこれは三角形$PBC$の内心なので，$PR$は$BPC$の二等分線です．また，$BP-CP=BH-CH$が成り立つので，$P$は$B,C$を焦点とし，$H$を通る双曲線上にあります．この双曲線を$\pi$としましょう．
上の$2$つの事実と，多少の二次曲線についての知識により$PR$は$\pi$の$P$での接線であることがわかります．
次に気づくこと
$AH\perp BC$かに関わらず，$AH:HR=AQ:QH$(すなわち$A,Q,R,H$は調和点列)が成り立ちます．
以上より，次のお気持ちになります．
もはや$B,C,E,F$は考えなくてもいいな、、
ということで次のことを示せば良いです．
双曲線$\pi : x^2-ay^2=1$上の点$H(1,0),P(x_0,y_0)\quad (x_0,y_0>0)$と，定点$A(0,b)$がある．$P$での$\pi$の接線と$AH$の交点を$R(1,w)$とし，$AH:HR=AQ:QH$を満たす線分$AR$上の点$Q$をとる．$P$の位置に関わらず直線$PQ$はある定点を通ることを示せ．
$x^2-ay^2=1$の両辺を$x$で微分することで$\dfrac{dy}{dx}=\dfrac{x}{ay}$を得る．したがって$\dfrac{y_0-w}{x_0-1}=\dfrac{x_0}{ay_0}$なので$x_0^2-ay_0^2=1$に注意して$w$について解くと，$w=\dfrac{x_0-1}{ay_0}$となる．
$Q(1,q)$とすると，$AH:HR=AQ:QH\Longleftrightarrow b:w=b-q:q-w$より，$q=\dfrac{b}{1+b/w}=\dfrac{b(x_0-1)}{x_0+aby_0-1}$を得る．
$PQ:(q-y_0)x+(x_0-1)y=x_0q-y_0$に先ほど求めた$q$を代入して整理すると$PQ:(bx_0+y_0)x-(x_0+aby_0-1)y=y_0+b$となる．(途中で$x_0^2-ay_0^2=1$を使っているので注意)
これは$P(x_0,y_0)$に関わらず定点$(\dfrac{1}{ab^2-1},\dfrac{b}{ab^2-1})$を通るので示された．$\square$
式が与えられている曲線の接線は扱いやすいので結構刺さります．$PR$を二等分線から接線に捉え直した時点で座標計算に分があると判断します．$3$段落の式整理は少し大変ですが，その途中に両辺を$x_0-1$で割る過程があり，そのおかげで得られる直線の式は$x_0,y_0$についての$1$次式となりました．勝ちを確信します．$x,y$をうまく調整すれば$x_0,y_0$を消せます．
以上がISL2022G6の解説になります．読んでいただきありがとうございました．
この記事を高評価した人
この記事に送られたバッジ
投稿者
