楕円と双曲線の準円を同時に求める
大学入試系の数学をやっているとたびたび現れる二次曲線の問題は, 同じような式を何個も並べて計算しないといけないことが多く面倒です.そこに行列の知識を加えて, できるだけ簡単な式で見通し良く解けるようになったらいいなと思っていました. その例として, 特に強烈にこの方法が刺さる, 準円を求める話をしていきたいと思います.
この記事ではベクトルの上付き矢印を省略します.
二次曲線$\frac {x^2} {a^2} \pm \frac {y^2} {b^2} = 1$は行列$A=\begin{pmatrix}
\frac 1 {a^2} & 0\\
0 & \pm\frac 1 {b^2}
\end{pmatrix}$とベクトル$x = \begin{pmatrix}x\\y\end{pmatrix}$ を用いて以下のように表現できる:
$$ x^\top A x=1$$
ベクトル$x$の$n$への正射影ベクトル$\mathrm{proj}_nx$は以下の通り:
$$ \mathrm{proj}_n x =\left(\frac{n \cdot x}{n \cdot n} \right)n$$
二次曲線$ x^\top A x=1$の$x$における法線ベクトルの一つは以下の通り:
$$Ax$$
$\frac {x^2} {a^2} \pm \frac {y^2} {b^2} = 1$という形式の二次曲線に限っては, 高校で扱う ”$(x_0,y_0)$における接線が$\frac {x_0} {a^2}x \pm \frac {y_0} {b^2}y = 1$” という定理より, 法線ベクトルのひとつは$ (\frac {x_0} {a^2}, \frac {y_0} {b^2})$と求められます.これを行列で表記すると上記を得ます.
それ以外の形式についても成り立ちますが今回は言及しません.
曲線$\frac{x^2}{a^2} \pm \frac{y^2}{b^2} =1$ 上の直交する二つの接線の交点の軌跡を求めよ
二つの接点を$ x_i \; (i=1,2)$, 接線の交点を$ p$とします.
図より, $x_i$の$Ax_i$への正射影(橙のベクトル)の和が交点のベクトル$p$になります:
$$ p= \sum_{i=1}^2\frac{A x_i \cdot x_i}{|A x_i|^2}A x_i = \sum_{i=1}^2\frac{A x_i \cdot x_i}{|A x_i|} e_i \quad \left(e_i= \frac{Ax_i}{|Ax_i|} \right) $$
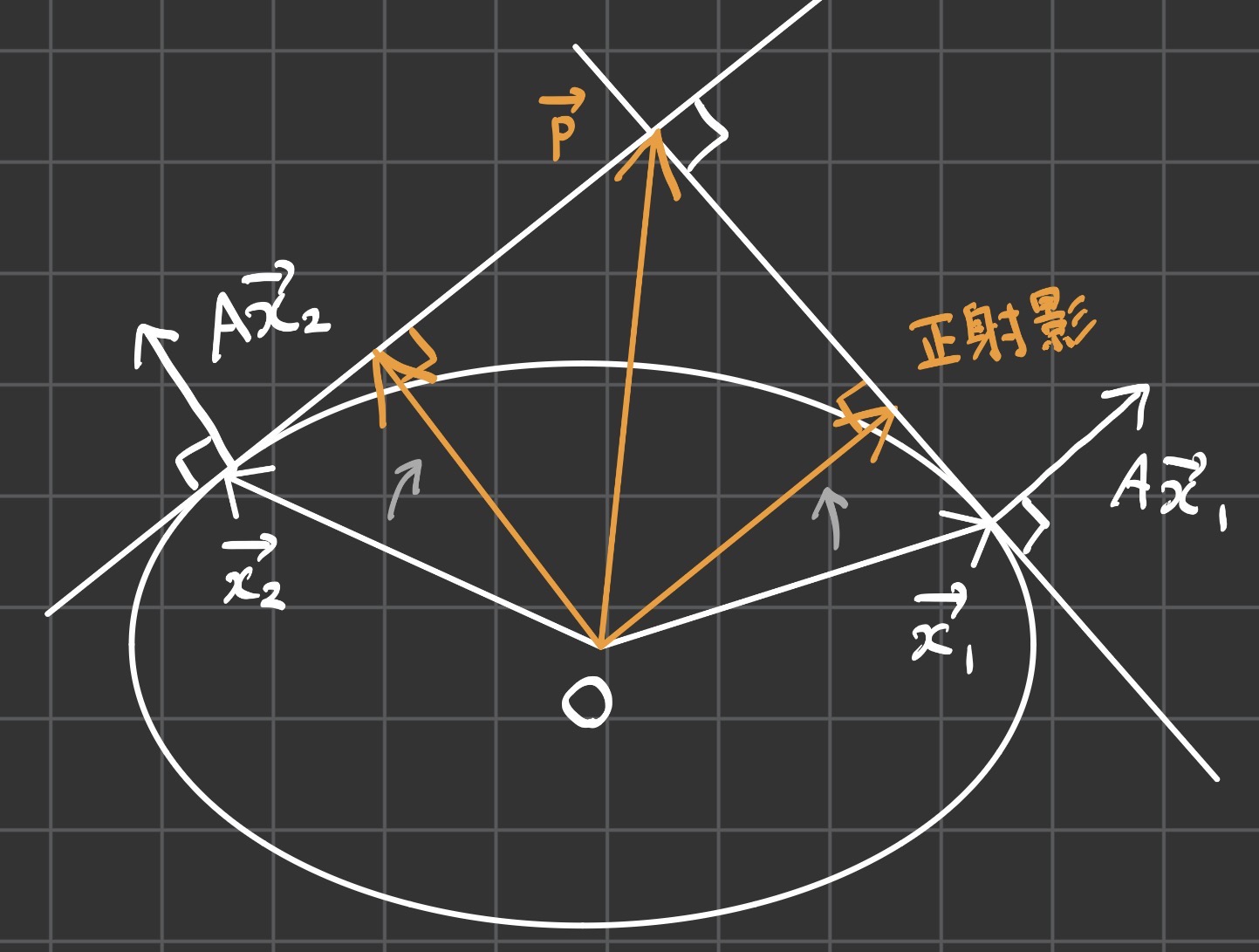正射影の和がpになる様子
$e_1,e_2$ は正規直交基底なので、$|p|^2$ は$p$の各成分の二乗の和で計算できます.
$x^\top Ax=Ax_i \cdot x_i=1, A^\top=A$ に注意して,
$$
\begin{align}
|p|^2 &= \sum_{i=1}^2\frac{x_i^\top Ax_i}{|Ax_i|^2} &(x_i\text{は曲線上なので}x_i^\top Ax_i=1)\\
&= \sum_{i=1}^2\frac{(Ax_i)^\top A^{-1}Ax_i}{|Ax_i|^2} \\
&= \sum_{i=1}^2 e_i^\top A^{-1} e_i \\
&=trA^{-1}
\end{align}
$$
よって求める軌跡は原点中心, 半径$\sqrt{a^2 \pm b^2}$の円になります.
$ a^2 - b^2 < 0$ のときは軌跡が存在しません
$a^2 - b^2 \geq 0$ のとき、円と漸近線の交点は双曲線における無限遠点における接線に相当するので除外しなければなりません
この記事を高評価した人
この記事に送られたバッジ
投稿者
