7
現代数学議論
f'(2x)=f'(x)f(x)
430
1
$$\newcommand{sint}[0]{\:\cancel{^{}}\!\!\!\:\:\:\llap{\int}}
$$
この問題はキャベ数🌂𝕄さんによって生み出された問題です。
キャベ数🌂𝕄さんのポスト
キャベ数🌂𝕄さんのポスト
はここから
\begin{eqnarray}
f'(2x) = f'(x)f(x) \\
f(x) = \sum_{i=0}^\infty a_ix^i
\end{eqnarray}
とすると、
\begin{eqnarray}
f'(x) &=& \sum_{i=1}^\infty ia_ix^{i-1} \\
f'(2x) &=& \sum_{i=1}^\infty ia_i(2x)^{i-1}
\\&=& \sum_{i=1}^\infty 2^{i-1}ia_ix^{i-1}
\end{eqnarray}
それと
\begin{eqnarray}
f'(x)f(x) = \qty(\sum_{i=1}^\infty ia_ix^{i-1})\qty(\sum_{i=0}^\infty a_ix^i)
\end{eqnarray}
これの$x^i$の項は
\begin{eqnarray}
\sum_{k=0}^{i} (k+1)a_{k+1}a_{i-k}
\end{eqnarray}
そして$f'(2x)$の$x^i$の項は
\begin{eqnarray}
2^i(i+1)a_{i+1}
\end{eqnarray}
よってこれらが同じなので
\begin{eqnarray}
2^i(i+1)a_{i+1} &=& \sum_{k=0}^i (k+1)a_{k+1}a_{i-k}
\end{eqnarray}
となる。
これ変形できて、
\begin{eqnarray}
2^i(i+1)a_{i+1} &=& \sum_{k=0}^i (k+1)a_{k+1}a_{i-k} \\
2^i(i+1)a_{i+1} &=& \qty(\sum_{k=0}^{i-1} \qty(k+1)a_{k+1}a_{i-k}) + (i+1)a_{i+1}a_0 \\
(i+1)a_{i+1}\qty(2^i-a_0) &=& \sum_{k=0}^{i-1} \qty(k+1)a_{k+1}a_{i-k} \\
(i+1)a_{i+1}\qty(2^i-a_0) &=& \sum_{k=1}^{i} ka_ka_{i+1-k}
\end{eqnarray}
関係図みたいなものを書くと
\begin{eqnarray}
[i+1][0] \longleftrightarrow [1][2][3]\cdots[i]
\end{eqnarray}
となるので、まぁ書き下すと分かりやすいですが、
\begin{eqnarray}
[2][0] &\longleftrightarrow& [1] \\
[3][0] &\longleftrightarrow& [1][2] \\
[4][0] &\longleftrightarrow& [1][2][3] \\
[5][0] &\longleftrightarrow& [1][2][3][4] \\
&\vdots&
\end{eqnarray}
となります。
最初の方はもうちょっと詳しく見たいですね。
\begin{eqnarray}
&x& \quad &x^0& \quad &x^1& \quad &x^2& \\
&f'(2x)& &2^01a_1& &2^12a_2& &2^23a_3& \\
&f'(x)f(x)& &1a_1a_0& &2a_2a_0+1a_1a_1& &3a_3a_0+2a_2a_1+1a_1a_2&
\end{eqnarray}
ぬぅ
縦にするといいかも
\begin{eqnarray}
2^01a_1 &=& 1a_1a_0 \\
2^12a_2 &=& 2a_2a_0+1a_1a_1 \\
2^23a_3 &=& 3a_3a_0+2a_2a_1+1a_1a_2 \\
2^34a_4 &=& 4a_4a_0+3a_3a_1+2a_2a_2+1a_1a_3 \\
&\downarrow& \\
0 &=& (a_0-1)a_1
\end{eqnarray}
なので$a_0$が$1$か$a_1$が$0$です。
そして$a_2$を求めるには$a_0$と$a_1$がいります。
困ったなぁ
$a_0=1$のとき
$a_1=t$とします。
この時
\begin{eqnarray} 4a_2 &=& 2a_2a_0+a_1^2 \\ 2a_2 &=& t^2 \\ a_2 &=& \frac{1}{2}t^2 \end{eqnarray}
ていうか一般に
\begin{eqnarray} (i+1)a_{i+1}\qty(2^i-a_0) &=& \sum_{k=1}^{i} ka_ka_{i+1-k} \\ &\downarrow& \\ (i+1)a_{i+1}\qty(2^i-1) &=& \sum_{k=1}^{i} ka_ka_{i+1-k} \\ &\downarrow& \\ a_{i+1} &=& \frac{1}{(i+1)\qty(2^i-1)}\sum_{k=1}^{i} ka_ka_{i+1-k} \end{eqnarray}
なので、
\begin{eqnarray} a_1 &=& t\\ a_{1+1} &=& \frac{1}{(1+1)\qty(2^1-1)}1a_1^2 \\ a_2 &=& \frac{1}{2}t^2 \\ a_{1+2} &=& \frac{1}{(2+1)\qty(2^2-1)}\qty(1a_1a_2+2a_2a_1) \\ a_3 &=& \frac{1}{9}\qty(\frac{1}{2}t^3+\frac{2}{2}t^3) \\ a_3 &=& \frac{1}{6}t^3 \end{eqnarray}
あ～
多分$a_n = \frac{1}{n!}t^n$ですね。
というか一つ気づいたのですが、
\begin{eqnarray}
&& \sum_{k=1}^{i} ka_ka_{i+1-k}
\\&=& 1a_1a_i + 2a_2a_{i-1} + 3a_3a_{i-2} + 4a_4a_{i-3} + \cdots + (i-1)a_{i-1}a_2 + ia_ia_1
\end{eqnarray}\begin{eqnarray}
&=& ia_ia_1 + (i-1)a_{i-1}a_2 + \cdots + 4a_4a_{i-3} + 3a_3a{i-2} + 2a_2a_{i-1} + 1a_1a_i
\end{eqnarray}
あ、
あ、、、
\begin{array}{rr} && 1a_1a_i &+& 2a_2a_{i-1} &+& \cdots &+& (i-1)a_{i-1}a_2 &+& ia_ia_1 \\ +\big{)}&& ia_ia_1 &+& (i-1)a_{i-1}a_2 &+& \cdots &+& 2a_2a_{i-1} &+& 1a_1a_i \\ \hline & &(i+1)a_ia_1 &+& (i+1)a_{i-1}a_2 &+& \cdots &+& (i+1)a_{i-1}a_2 &+& (i+1)a_ia_1 \end{array}\begin{eqnarray} \Rightarrow (i+1)\qty(a_ia_1+a_{i-1}a_2+\cdots+a_{i-1}a_2+a_ia_1) \end{eqnarray}
つまり
\begin{eqnarray} 2\sum_{k=1}^{i} ka_ka_{i+1-k} &=& (i+1)\sum_{k=1}^i a_ka_{i+1-k} \end{eqnarray}
あ、
あ、、、
\begin{array}{rr} && 1a_1a_i &+& 2a_2a_{i-1} &+& \cdots &+& (i-1)a_{i-1}a_2 &+& ia_ia_1 \\ +\big{)}&& ia_ia_1 &+& (i-1)a_{i-1}a_2 &+& \cdots &+& 2a_2a_{i-1} &+& 1a_1a_i \\ \hline & &(i+1)a_ia_1 &+& (i+1)a_{i-1}a_2 &+& \cdots &+& (i+1)a_{i-1}a_2 &+& (i+1)a_ia_1 \end{array}\begin{eqnarray} \Rightarrow (i+1)\qty(a_ia_1+a_{i-1}a_2+\cdots+a_{i-1}a_2+a_ia_1) \end{eqnarray}
つまり
\begin{eqnarray} 2\sum_{k=1}^{i} ka_ka_{i+1-k} &=& (i+1)\sum_{k=1}^i a_ka_{i+1-k} \end{eqnarray}
というわけで、
\begin{eqnarray} a_{i+1} &=& \frac{1}{(i+1)\qty(2^i-1)}\sum_{k=1}^{i} ka_ka_{i+1-k} \\ &\downarrow& \\ a_{i+1} &=& \frac{1}{2\qty(2^i-1)}\sum_{k=1}^i a_ka_{i+1-k} \end{eqnarray}
となります。
じゃぁ証明
\begin{eqnarray}
a_n = \frac{1}{n!}t^n
\end{eqnarray}
であることを証明する。
帰納法で。
よって$(\mathrm{i})$と$(\mathrm{ii})$より示されました。
であることを証明する。
帰納法で。
$(\mathrm i)$ $n=1$のとき
\begin{eqnarray} a_1 &=& t \\ \frac{1}{1!}t^1 &=& t \end{eqnarray}
よりあっている。
\begin{eqnarray} a_1 &=& t \\ \frac{1}{1!}t^1 &=& t \end{eqnarray}
よりあっている。
$(\mathrm {ii})$ $n\le k$のときあっていると仮定したときの$n=k+1$のとき
\begin{eqnarray} a_n &=& \frac{1}{n!}t^n \end{eqnarray}
が$n=1\sim k$で成立すると仮定する。
この時$n=k+1$は
\begin{eqnarray} a_{k+1} &=& \frac{1}{2\qty(2^k-1)}\sum_{r=1}^k a_ra_{k+1-r} \\&=& \frac{1}{2\qty(2^k-1)}\sum_{r=1}^k \frac{t^r}{r!}\frac{t^{k+1-r}}{(k+1-r)!} \\&=& \frac{t^{k+1}}{2\qty(2^k-1)}\sum_{r=1}^k \frac{1}{r!}\frac{1}{(k+1-r)!} \\&=& \frac{t^{k+1}}{2(k+1)!\qty(2^k-1)}\sum_{r=1}^k \frac{(k+1)!}{r!(k+1-r)!} \end{eqnarray}
ここで二項係数が出てきましたね。
日本では${}_nC_k$で親しまれていますが、私は$\binom{n}{k}$と書きます。
\begin{eqnarray} &=& \frac{t^{k+1}}{2(k+1)!\qty(2^k-1)}\sum_{r=1}^k \binom{k+1}{r} \end{eqnarray}
よって
\begin{eqnarray} && \frac{t^{k+1}}{2(k+1)!\qty(2^k-1)}\sum_{r=1}^k \binom{k+1}{r} \\&=& \frac{t^{k+1}}{2(k+1)!\qty(2^k-1)}\qty(2^{k+1}-2) \\&=& \frac{t^{k+1}}{(k+1)!} \end{eqnarray}
\begin{eqnarray} a_n &=& \frac{1}{n!}t^n \end{eqnarray}
が$n=1\sim k$で成立すると仮定する。
この時$n=k+1$は
\begin{eqnarray} a_{k+1} &=& \frac{1}{2\qty(2^k-1)}\sum_{r=1}^k a_ra_{k+1-r} \\&=& \frac{1}{2\qty(2^k-1)}\sum_{r=1}^k \frac{t^r}{r!}\frac{t^{k+1-r}}{(k+1-r)!} \\&=& \frac{t^{k+1}}{2\qty(2^k-1)}\sum_{r=1}^k \frac{1}{r!}\frac{1}{(k+1-r)!} \\&=& \frac{t^{k+1}}{2(k+1)!\qty(2^k-1)}\sum_{r=1}^k \frac{(k+1)!}{r!(k+1-r)!} \end{eqnarray}
ここで二項係数が出てきましたね。
日本では${}_nC_k$で親しまれていますが、私は$\binom{n}{k}$と書きます。
\begin{eqnarray} &=& \frac{t^{k+1}}{2(k+1)!\qty(2^k-1)}\sum_{r=1}^k \binom{k+1}{r} \end{eqnarray}
ここで、二項係数の定義である
\begin{eqnarray} (x+y)^a = \sum_{r=0}^a \binom{a}{r}x^{a-r}y^r \end{eqnarray}
に$x=1,y=1,a=k+1$をぶち込むと
\begin{eqnarray} 2^{k+1} = \sum_{r=0}^{k+1} \binom{k+1}{r} \end{eqnarray}
余計なものがありますね。$r=0$の時と$r=k+1$の時を引きましょう
\begin{eqnarray} 2^{k+1}-\binom{k+1}{k+1}-\binom{k+1}{0} &=& \sum_{r=1}^k \binom{k+1}{r} \\ 2^{k+1}-2&=& \sum_{r=1}^k \binom{k+1}{r} \end{eqnarray}
\begin{eqnarray} (x+y)^a = \sum_{r=0}^a \binom{a}{r}x^{a-r}y^r \end{eqnarray}
に$x=1,y=1,a=k+1$をぶち込むと
\begin{eqnarray} 2^{k+1} = \sum_{r=0}^{k+1} \binom{k+1}{r} \end{eqnarray}
余計なものがありますね。$r=0$の時と$r=k+1$の時を引きましょう
\begin{eqnarray} 2^{k+1}-\binom{k+1}{k+1}-\binom{k+1}{0} &=& \sum_{r=1}^k \binom{k+1}{r} \\ 2^{k+1}-2&=& \sum_{r=1}^k \binom{k+1}{r} \end{eqnarray}
よって
\begin{eqnarray} && \frac{t^{k+1}}{2(k+1)!\qty(2^k-1)}\sum_{r=1}^k \binom{k+1}{r} \\&=& \frac{t^{k+1}}{2(k+1)!\qty(2^k-1)}\qty(2^{k+1}-2) \\&=& \frac{t^{k+1}}{(k+1)!} \end{eqnarray}
よって$(\mathrm{i})$と$(\mathrm{ii})$より示されました。
なので$n=0$の時も$\frac{1}{0!}t^0=1$となって合致していますので、
$a_0=1$の時は
\begin{eqnarray} f(x) &=& \sum_{n=0}^{\infty}\frac{t^n}{n!}x^n \\&=& e^{tx} \end{eqnarray}
と分かりました。
はいつぎぃ
$a_1=0$
What happens in this case?
この場合はどうなるのでしょうか？
$a_0=t$とします。
\begin{eqnarray} 4a_2&=&2a_2a_0+a_1^2 \\ 4a_2-2a_2t &=& 0 \\ 2a_2\qty(2-t) &=& 0 \end{eqnarray}
ということで、$t=2$または$a_2=0$となりました。
$t=2$のとき
これはどうなるでしょうか？$a_2=t_2$としましょう
\begin{eqnarray} 2^23a_3 &=& 3a_3a_0+2a_2a_1+1a_1a_2 \\ 12a_3 &=& 6a_3+2t_20+1\cdot0\cdot t_2 \\ a_3 &=& 0 \end{eqnarray}
$a_4$はどう？
\begin{eqnarray} 2^34a_4 &=& 4a_4a_0+3a_3a_1+2a_2a_2+1a_1a_3 \\ 32a_4 &=& 8a_4 +2t_2^2 \\ a_4 &=& \frac{1}{12}t_2^2 \end{eqnarray}
見えてきませんね？
\begin{eqnarray} 2^45a_5 &=& 5a_5a_0+4a_4a_1+3a_3a_2+2a_2a_3+1a_1a_4 \\ 80a_5 &=& 10a_5 \\ a_5 &=& 0 \end{eqnarray}
んん？？？
\begin{eqnarray} 2^56a_6 &=& 6a_6a_0+5a_5a_1+4a_4a_2+3a_3a_3+2a_2a_4+1a_1a_5 \\ 192a_6 &=& 12a_6 + \frac{6}{12}t_2^3 \\ 180a_6 &=& \frac{1}{2}t_2^3 \\ a_6 &=& \frac{1}{360}t_2^3 \end{eqnarray}
う～ん。$\frac{(2n)!}{2}$かな？
\begin{eqnarray} 2^67a_7 &=& 7a_7a_0+6a_6a_1+5a_5a_2+4a_4a_3+3a_3a_4+2a_2a_5+1a_1a_6 \\ 448a_7 &=& 14a_7 + 0 \\ a_7 &=& 0 \end{eqnarray}
\begin{eqnarray} 2^78a_8 &=& 8a_8a_0+7a_7a_1+6a_6a_2+5a_5a_3+4a_4a_4+3a_3a_5+2a_2a_6+1a_1a_7 \\ 1024a_8 &=& 16a_8+\frac{8}{360}t_2^4+\frac{4}{144}t_2^4 \\ 1008a_8 &=& \frac{1}{20}t_2^4 \\ a_8 &=& \frac{1}{20160}t_2^4 \\ \end{eqnarray}
これもう$\frac{(2n)!}{2}$でしょ
$a_{2n-1}=0$
では証明していきましょう$\mathrm{(i)}$ $n=1$のとき
\begin{eqnarray} a_1 = 0 \end{eqnarray}
なので成立
$\mathrm{(ii)}$ $n\le k$で成立すると仮定する。
この時の$n=k+1$を調べる
\begin{eqnarray} (i+1)a_{i+1}\qty(2^i-a_0) &=& \sum_{k=1}^{i} ka_ka_{i+1-k} \\ a_{i+1} &=& \frac{1}{(i+1)\qty(2^i-a_0)}\sum_{k=1}^i ka_ka_{i+1-k} \\ a_{i+1} &=& \frac{1}{2\qty(2^i-a_0)} \sum_{k=1}^i a_ka_{i+1-k} \\ \end{eqnarray}
なので
\begin{eqnarray} a_{2k+1} &=&\frac{1}{2^{2k+1}-2t} \sum_{i=1}^{2k} a_ia_{2k+1-i} \\&=& \frac{1}{2^{2k+1}-2t}\qty(a_1a_{2k}+a_2a_{2k-1}+a_3a_{2k-2}+a_4a_{2k-3}+\cdots) \\&=& \frac{1}{2^{2k+1}-2t}\qty(0a_{2k}+a_20+0a_{2k-2}+a_40+\cdots) \\&=& 0 \end{eqnarray}
よって$a_{2n-1}=0$と分かりました
$a_{2n}=\frac{2}{(2n)!}t_2^{n}$
$\mathrm{(i)}$ $n=0$のとき\begin{eqnarray} a_{0} = \frac{2}{0!}t_2^0 = 2 \end{eqnarray}
なので正しい
$\mathrm{(ii)}$ $n\le k$で成立すると仮定
すると$n=k+1$の時
\begin{eqnarray} a_{2k+2} &=& \frac{1}{2\qty(2^{2k+1}-2)}\sum_{i=1}^{2k+1} a_ia_{2k+2-i} \\&=& \frac{1}{2^{2k+2}-4}\qty(a_1a_{2k+1}+a_2a_{2k}+a_3a_{2k-1}+a_4a_{2k-2}\cdots) \\&=& \frac{1}{2^{2k+2}-4}\qty(0+a_2a_{2k}+0+a_4a_{2k-2}+0+\cdots) \\&=& \frac{1}{2^{2k+2}-4}\sum_{i=1}^k a_{2i}a_{2(k+1-i)} \\&=& \frac{1}{2^{2k+2}-4}\sum_{i=1}^k \frac{2}{(2i)!}t_2^i \frac{2}{(2(k+1-i))!}t_2^{k+1-i} \\&=& \frac{t_2^{k+1}}{2^{2k+2}-4}\sum_{i=1}^k \frac{4}{(2i)!(2k+2-2i)!} \\&=& \frac{t_2^{k+1}}{(2^{2k}-1)(2k+2)!}\sum_{i=1}^k \frac{(2k+2)!}{(2i)!(2k+2-2i)!} \\&=& \frac{t_2^{k+1}}{(2^{2k}-1)(2k+2)!}\sum_{i=1}^k \binom{2k+2}{2i} \end{eqnarray}
ここで、さっきの
\begin{eqnarray} (x+y)^a = \sum_{r=0}^a \binom{a}{r}x^{a-r}y^r \end{eqnarray}
に$x=1,y=1,a=2k$を入れると
\begin{eqnarray} 2^{2k} = \sum_{i=0}^{2k} \binom{2k}{i} \end{eqnarray}
そして、$x=1,y=-1,a=2k$を入れると
\begin{eqnarray} (1+(-1))^{2k} &=& \sum_{i=0}^{2k} (-1)^i\binom{2k}{i} \\ 0 &=& \sum_{i=0}^{2k} (-1)^i\binom{2k}{i} \end{eqnarray}
これらを足し合わせると、$i$が奇数の時だけ消えるんですよね(うれしい)
なので足し算する個数が$2k$個から$k$個になるのに注意してください
\begin{eqnarray} 2^{2k} &=& \sum_{i=0}^{k}2\binom{2k}{2i} \\ 2^{2k-1} &=& \sum_{i=0}^k \binom{2k}{2i} \end{eqnarray}となります。
ここから$k$を$k+1$に変えると
\begin{eqnarray} 2^{2k+1} &=& \sum_{i=0}^{k+1} \binom{2k+2}{2i} \end{eqnarray}
そして$i=k+1$と$i=0$を引くと
\begin{eqnarray} 2^{2k+1}-2 &=& \sum_{i=0}^{k+1} \binom{2k+2}{2i} \end{eqnarray}
\begin{eqnarray} (x+y)^a = \sum_{r=0}^a \binom{a}{r}x^{a-r}y^r \end{eqnarray}
に$x=1,y=1,a=2k$を入れると
\begin{eqnarray} 2^{2k} = \sum_{i=0}^{2k} \binom{2k}{i} \end{eqnarray}
そして、$x=1,y=-1,a=2k$を入れると
\begin{eqnarray} (1+(-1))^{2k} &=& \sum_{i=0}^{2k} (-1)^i\binom{2k}{i} \\ 0 &=& \sum_{i=0}^{2k} (-1)^i\binom{2k}{i} \end{eqnarray}
これらを足し合わせると、$i$が奇数の時だけ消えるんですよね(うれしい)
なので足し算する個数が$2k$個から$k$個になるのに注意してください
\begin{eqnarray} 2^{2k} &=& \sum_{i=0}^{k}2\binom{2k}{2i} \\ 2^{2k-1} &=& \sum_{i=0}^k \binom{2k}{2i} \end{eqnarray}となります。
ここから$k$を$k+1$に変えると
\begin{eqnarray} 2^{2k+1} &=& \sum_{i=0}^{k+1} \binom{2k+2}{2i} \end{eqnarray}
そして$i=k+1$と$i=0$を引くと
\begin{eqnarray} 2^{2k+1}-2 &=& \sum_{i=0}^{k+1} \binom{2k+2}{2i} \end{eqnarray}
よって
\begin{eqnarray} a_{2k+2} &=& \frac{t_2^{k+1}}{2^{2k}-1}\sum_{i=1}^k \binom{2k+2}{2i} \\&=& \frac{t_2^{k+1}}{(2^{2k}-1)(2k+2)!}\qty(2^{2k+1}-2) \\&=& \frac{2}{(2k+2)!}t_2^{k+1} \end{eqnarray}
なので証明できました！
これは結局どうなるんですか？
\begin{eqnarray} f(x) &=& \frac{2}{0!}t^0 + \frac{2}{2!}t^1x^2 + \frac{2}{4!}t^2x^4 + \frac{2}{6!}t^3x^6 \cdots \\ &=& e^{-\sqrt{t} x} + e^{\sqrt{t} x} \\ &=& 2 \cosh(\sqrt{t} x) \end{eqnarray}
ふう。でもこれではまだ終わっていません
$a_2=0$のとき
\begin{eqnarray} 2^23a_3 &=& 3a_3a_0 + 2a_2a_1 + 1a_1a_2 \\ 12a_3 &=& 3a_3a_0 \\ 3a_3(a_0-4) &=& 0 \\ 3a_3(t-4) &=& 0 \end{eqnarray}
え～
またか
また分岐ですか？嫌になっちゃいますね。
でもさっきと同じような雰囲気が醸し出されているのですが、どうにかならないでしょうか？
帰納法で行くしかないかなぁ
ぱたーんを特定する
(仮定) えーと$1\le i\le k$に対して$a_i=0$だとし、$a_0=t$とします。
\begin{eqnarray} (k+1)a_{k+1}\qty(2^k-a_0) &=& \sum_{i=1}^{k} ia_ia_{k+1-i} \end{eqnarray}
なので、
\begin{eqnarray} (k+1)a_{k+1}(2^k-t) &=& 0 \end{eqnarray}
よって、(仮定)からは$a_{k+1}=0$または$t=2^k$の二つのパターンが生えることが分かりました。
そして、今$a_1=0$で$a_0=t$な状態が今生えているので、
結局
\begin{align} a_0=t=2^k \;\;\;,\;\;\; a_1=a_2=a_3=\cdots=a_k=0 \end{align}
のパターンが$k=1,2,\cdots$と生えるわけです。
よし、パターン特定終了！
物語を終わらせに行く
\begin{eqnarray}
a_0=2^k \;\;\;,\;\;\; a_1=a_2=a_3=\cdots=a_k=0 \;\;\;.\;\;\; a_{k+1} = t
\end{eqnarray}
という仮定のもと解いていきます。
\begin{eqnarray}
a_{n+1} &=& \frac{1}{2\qty(2^n-a_0)} \sum_{i=1}^n a_ia_{n+1-i} \\
\end{eqnarray}
なので、
\begin{eqnarray} a_{k+2} &=& \frac{1}{2\qty(2^{k+1}-2^k)}\sum_{i=1}^{k+1} a_ia_{k+2-i} \\&=& \frac{1}{2\qty(2^{k+1}-2^k)} \cdot 0 \\&=& 0 \end{eqnarray}
というより、$1\le c\le k$に対して、
\begin{eqnarray} a_{k+c+1} &=& \frac{1}{2\qty(2^{k+c}-2^k)}\sum_{i=1}^{k+c} a_ia_{k+c+1-i} \\&=& \frac{1}{2\qty(2^{k+1}-2^k)} \cdot 0 \\&=& 0 \end{eqnarray}
です。
そして、$a_{2k+2}$で、
\begin{eqnarray} a_{2k+2} &=& \frac{1}{2\qty(2^{2k+1}-2^k)}\sum_{i=1}^{2k+1} a_ia_{2k+2-i} \\&=& \frac{1}{2^{2k+2}-2^{k+1}}a_{k+1}^2 \\&=& \frac{1}{2^{k+1}(2^{k+1}-1)}t^2 \end{eqnarray}
多分これも$a_0,a_{k+1},a_{2(k+1)},a_{3(k+1)},a_{4(k+1)},\cdots$以外全部$0$なんでしょうね
は～
じゃぁ$1\le b'\le b$において$a_{n} \;\;(1\le n \le b(k+1))$は$a_{b'(k+1)}$を除いて全部$0$だったとしましょう。
すると$0\le c \le k-1$をとって、
\begin{eqnarray} a_{b(k+1)+c+1} &=& \frac{1}{2\qty(2^{b(k+1)+c}-2^k)} \sum_{i=1}^{b(k+1)+c} a_ia_{b(k+1)+c+1-i} \end{eqnarray}
ここで、右辺のシグマは$i=b'(k+1)$以外の時$a_i$が$0$になります。
逆に、$i=b'(k+1)$と表されるとき、$a_{b(k+1)+c+1-i}=a_{(b-b')(k+1)+c+1}$となり、$1\le c+1\le k$ですから、$a_{(b-b')(k+1)+c+1}$は$a_{b(k+1)}$のような、
添え字が$k+1$の倍数にはなりえません。
よって$a_{b(k+1)+c+1-i}$がこの時$0$になります。
結局はどんな$i$をとってきてもどちらかは必ず$0$になるのです。
よって
\begin{eqnarray} a_{b(k+1)+c+1} &=& \frac{1}{2\qty(2^{b(k+1)+c}-2^k)}\cdot 0 \\&=& 0 \end{eqnarray}
あとは$b=1$に当たる場合ですが、$a_n (1\le n\le k+1)$は確かに$a_{k+1}$を除いてみんな$0$です。
よって帰納法より、$a_0,a_{k+1},a_{2(k+1)},a_{3(k+1)},a_{4(k+1)},\cdots$以外全部$0$であると言えました。
なので、
\begin{eqnarray} a_{k+2} &=& \frac{1}{2\qty(2^{k+1}-2^k)}\sum_{i=1}^{k+1} a_ia_{k+2-i} \\&=& \frac{1}{2\qty(2^{k+1}-2^k)} \cdot 0 \\&=& 0 \end{eqnarray}
というより、$1\le c\le k$に対して、
\begin{eqnarray} a_{k+c+1} &=& \frac{1}{2\qty(2^{k+c}-2^k)}\sum_{i=1}^{k+c} a_ia_{k+c+1-i} \\&=& \frac{1}{2\qty(2^{k+1}-2^k)} \cdot 0 \\&=& 0 \end{eqnarray}
です。
そして、$a_{2k+2}$で、
\begin{eqnarray} a_{2k+2} &=& \frac{1}{2\qty(2^{2k+1}-2^k)}\sum_{i=1}^{2k+1} a_ia_{2k+2-i} \\&=& \frac{1}{2^{2k+2}-2^{k+1}}a_{k+1}^2 \\&=& \frac{1}{2^{k+1}(2^{k+1}-1)}t^2 \end{eqnarray}
多分これも$a_0,a_{k+1},a_{2(k+1)},a_{3(k+1)},a_{4(k+1)},\cdots$以外全部$0$なんでしょうね
は～
じゃぁ$1\le b'\le b$において$a_{n} \;\;(1\le n \le b(k+1))$は$a_{b'(k+1)}$を除いて全部$0$だったとしましょう。
すると$0\le c \le k-1$をとって、
\begin{eqnarray} a_{b(k+1)+c+1} &=& \frac{1}{2\qty(2^{b(k+1)+c}-2^k)} \sum_{i=1}^{b(k+1)+c} a_ia_{b(k+1)+c+1-i} \end{eqnarray}
ここで、右辺のシグマは$i=b'(k+1)$以外の時$a_i$が$0$になります。
逆に、$i=b'(k+1)$と表されるとき、$a_{b(k+1)+c+1-i}=a_{(b-b')(k+1)+c+1}$となり、$1\le c+1\le k$ですから、$a_{(b-b')(k+1)+c+1}$は$a_{b(k+1)}$のような、
添え字が$k+1$の倍数にはなりえません。
よって$a_{b(k+1)+c+1-i}$がこの時$0$になります。
結局はどんな$i$をとってきてもどちらかは必ず$0$になるのです。
よって
\begin{eqnarray} a_{b(k+1)+c+1} &=& \frac{1}{2\qty(2^{b(k+1)+c}-2^k)}\cdot 0 \\&=& 0 \end{eqnarray}
あとは$b=1$に当たる場合ですが、$a_n (1\le n\le k+1)$は確かに$a_{k+1}$を除いてみんな$0$です。
よって帰納法より、$a_0,a_{k+1},a_{2(k+1)},a_{3(k+1)},a_{4(k+1)},\cdots$以外全部$0$であると言えました。
あとは最後です。
$a_{3k+3}$はどうなるのでしょうか？
\begin{eqnarray} a_{n+1} &=& \frac{1}{2\qty(2^n-a_0)} \sum_{i=1}^n a_ia_{n+1-i} \\ a_{n+1} &=& \frac{1}{2^{n+1}-2a_0} \sum_{i=1}^n a_ia_{n+1-i} \\ a_{3k+3} &=& \frac{1}{2\qty(2^{3k+2}-2^k)}\sum_{i=1}^{3k+2} a_ia_{3k+3-i} \\&=& \frac{1}{2\qty(2^{3k+2}-2^k)}\qty(a_{k+1}a_{2k+2}+a_{2k+2}a_{k+1}) \\&=& \frac{1}{2^{3k+3}-2^{k+1}}\qty(t\frac{1}{2^{2k+2}-2^{k+1}}t^2+\frac{1}{2^{2k+2}-2^{k+1}}t^2\cdot t) \\&=& \frac{1}{2^{3k+3}-2^{k+1}}\qty(\frac{2t^3}{2^{2k+2}-2^{k+1}}) \\&=& \frac{2t^3}{(2^{3k+3}-2^{k+1})(2^{2k+2}-2^{k+1})} \end{eqnarray}
ほう(｀・ω・´)
\begin{eqnarray} a_{4k+4} &=& \frac{1}{2^{4k+4}-2^{k+1}}\sum_{i=1}^{4k+3} a_ia_{4k+4-i} \\&=& \frac{1}{2^{4k+4}-2^{k+1}}\qty(a_{k+1}a_{3k+3}+a_{2k+2}a_{2k+2}+a_{k+1}a_{3k+3}) \\&=& \frac{1}{2^{4k+4}-2^{k+1}}\qty(2a_{k+1}a_{3k+3}+\qty(a_{2k+2})^2) \\&=& \frac{1}{2^{4k+4}-2^{k+1}}\qty(\frac{4t^4}{(2^{3k+3}-2^{k+1})(2^{2k+2}-2^{k+1})}+\frac{t^4}{\qty(2^{2k+2}-2^{k+1})^2}) \\&=& \frac{1}{2^{4k+4}-2^{k+1}}\qty(\frac{4t^4\qty(2^{2k+2}-2^{k+1})}{\qty(2^{3k+3}-2^{k+1})\qty(2^{2k+2}-2^{k+1})^2}+\frac{\qty(2^{3k+3}-2^{k+1})t^4}{\qty(2^{3k+3}-2^{k+1})\qty(2^{2k+2}-2^{k+1})^2}) \\&=& \frac{1}{2^{4k+4}-2^{k+1}}\qty(\frac{4t^4\qty(2^{2k+2}-2^{k+1})+\qty(2^{3k+3}-2^{k+1})t^4}{\qty(2^{3k+3}-2^{k+1})\qty(2^{2k+2}-2^{k+1})^2}) \\&=& \frac{1\cdot2^{3k+3}+4\cdot2^{2k+2}-5\cdot2^{k+1}}{\qty(2^{4k+4}-2^{k+1})\qty(2^{3k+3}-2^{k+1})\qty(2^{2k+2}-2^{k+1})^2}t^4 \end{eqnarray}
ん、だいぶ見にくいですね。
ここは$A_t=2^{t(k+1)}-2^{k+1}$とでも置きましょうか
\begin{eqnarray} a_{4k+4} &=& \frac{A_3+4A_2}{A_4A_3A_2^2}t^4 \end{eqnarray}
ああ～きれい
まとめると
\begin{eqnarray} a_{k+1} &=& t \\ a_{2k+2} &=& \frac{1}{A_2}t^2 \\ a_{3k+3} &=& \frac{2}{A_3A_2}t^3 \\ a_{4k+4} &=& \frac{A_3+4A_2}{A_4A_3A_2^2}t^4 \end{eqnarray}
ん～ 見えそうで見えない
\begin{eqnarray} a_{5k+5} &=& \frac{1}{A_5}\qty(a_{k+1}a_{4k+4}+a_{2k+2}a_{3k+3}+a_{3k+3}a_{2k+2}+a_{4k+4}a_{k+1}) \\&=& \frac{1}{A_5}\qty(2a_{k+1}a_{4k+4}+2a_{2k+2}a_{3k+3}) \\&=& \frac{2}{A_5}\qty(\frac{A_3+4A_2}{A_4A_3A_2^2}t^5+ \frac{1}{A_2}\frac{2}{A_3A_2}t^5) \\&=& \frac{2}{A_5} \qty(\frac{A_3+4A_2}{A_4A_3A_2^2}t^5+ \frac{2}{A_3A_2^2}t^5) \\&=& \frac{2}{A_5} \qty(\frac{A_3+4A_2}{A_4A_3A_2^2}t^5+ \frac{2A_4}{A_4A_3A_2^2}t^5) \\&=& \frac{2}{A_5} \qty(\frac{2A_4+A_3+4A_2}{A_4A_3A_2^2}t^5) \\&=& \frac{4A_4+2A_3+8A_2}{A_5A_4A_3A_2^2}t^5 \end{eqnarray}
\begin{eqnarray} a_{6k+6} &=& \frac{1}{A_6}\qty(a_{k+1}a_{5k+5}+a_{2k+2}a_{4k+4}+a_{3k+3}a_{3k+3}+a_{4k+4}a_{2k+2}+a_{5k+5}a_{k+1}) \\&=& \frac{1}{A_6}\qty(2a_{k+1}a_{5k+5}+2a_{2k+2}a_{4k+4}+a_{3k+3}^2) \\&=& \frac{1}{A_6}\qty(2\frac{4A_4+2A_3+8A_2}{A_5A_4A_3A_2^2}t^6+2\frac{1}{A_2}\frac{A_3+4A_2}{A_4A_3A_2^2}t^6+\frac{4}{A_3^2A_2^2}t^6) \\&=& \frac{1}{A_6}\qty(\frac{8A_4A_3A_2+4A_3^2A_2+16A_3A_2^2+2A_5A_3^2+8A_5A_3A_2+4A_5A_4A_2}{A_5A_4A_3^2A_2^3})t^6 \\&=& \end{eqnarray}
ちょっと待てや
え？
え？？
法則性は？
$k=0,1$での階乗の法則性はどこに行ったのでしょうか。。。
---
考えてみましょう
とりあえず$a_{s(k+1)}=b_s$とします。めんどいので。
あと
\begin{eqnarray} A_t = \frac{1}{2^{t(k+1)}-2^{k+1}} \end{eqnarray}
にしておきます。
\begin{eqnarray} b_1 &=& t \\ b_2 &=& A_2(b_1b_1) \\&=& A_2t^2 \\ b_3 &=& A_3(b_1b_2 + b_2b_1) \\&=& A_3(2A_2t^3) \\&=& 2A_3A_2t^3 \\ b_4 &=& A_4(b_1b_3+b_2b_2+b_3b_1) \\&=& A_4(4A_3A_2t^4+A_2^2t^4) \\&=& A_4(4A_3A_2+A_2^2)t^4 \end{eqnarray}
もう$b_s$には$t^s$がつくというのが分かるので$t$は書きません。
\begin{eqnarray} b_1 &=& 1 \\ b_2 &=& A_2 \\ b_3 &=& A_32A_2 \\ b_4 &=& A_4(2A_32A_2+A_2^2) \\ b_5 &=& A_5(b_4b_1+b_3b_2+b_2b_3+b_1b_4) \\&=& A_5(2A_4(2A_32A_2+A_2^2)+2A_32A_2A_2) \\ b_6&=& A_6(2A_5(2A_4(2A_32A_2+A_2^2)+2A_32A_2A_2)+2A_4(2A_32A_2+A_2^2)A_2+(A_32A_2)^2) \end{eqnarray}
どうして
どうしてこんなにも不思議なものを生み出してしまうのでしょうか？
それは単に毎回先頭に$A_n$を掛けているからですね。
じゃぁどうやって次を予測すればいいのでしょうか？
\begin{eqnarray} b_n &=& A_n\sum_{i=1}^{n} b_ib_{n+1-i} \\ \downarrow \\ b_{n+1} &=& A_{n+1} \sum_{i=1}^{n+1} b_ib_{n+2-i} \end{eqnarray}
まず普通に考えて$b_ib_{n+1-i}$と$b_ib_{n+2-i}$との関係性は今知りたいものなのでわかっていません。
ぬぅ。
\begin{eqnarray} b_n &\leftarrow& A_n &&(b_1b_{n\;\;\;\:\:}&+&b_2b_{n-1}&+&b_3b_{n-2}&+&b_4b_{n-3}&+&b_5b_{n-4}\cdots) \\ b_{n+1} &\leftarrow& A_{n+1} &&(b_1b_{n+1}&+&b_2b_{n\;\;\;\:\:}&+&b_3b_{n-1}&+&b_4b_{n-2}&+&b_5b_{n-3}\cdots) \end{eqnarray}
↑展開した
\begin{eqnarray} && |&b_1& |&b_2& |&b_3& \\ \hline&b_1&|&b_1b_1&|&b_1b_2&|&\color{red}b_1b_3& \\ \hline&b_2&|&b_2b_1&|&\color{red}b_2b_2&|&b_2b_3& \\ \hline&b_3&|&\color{red}b_3b_1&|&b_3b_2&|&b_3b_3& \\ &\downarrow& \end{eqnarray}
\begin{eqnarray} && |&b_1& |&b_2& |&b_3& |&b_4& \\ \hline&b_1&|&b_1b_1&|&b_1b_2&|&b_1b_3&|&\color{red}b_1b_4& \\ \hline&b_2&|&b_2b_1&|&b_2b_2&|&\color{red}b_2b_3&|&b_2b_4& \\ \hline&b_3&|&b_3b_1&|&\color{red}b_3b_2&|&b_3b_3&|&b_3b_4& \\ \hline&b_4&|&\color{red}b_4b_1&|&b_4b_2&|&b_4b_3&|&b_4b_4& \\ \end{eqnarray}
こういうこと
斜めにすると
\begin{eqnarray} &b_1b_1& &&& &&& &&& &&b_1b_1& \\ &b_2b_1\;b_1b_2& &&& &&& &&& &&b_2b_1\;b_1b_2& \\ &b_3b_1\;b_2b_2\;b_1b_3& \quad&&+&\quad&&& \quad&&=&\quad&&b_3b_1\;b_2b_2\;b_1b_3& \\ &b_3b_2\;b_2b_3& &&& &&b_4b_1\;b_1b_4& &&& &&b_4b_1\;b_3b_2\;b_2b_3\;b_1b_4& \\ &b_3b_3& &&& &&b_4b_2\;b_2b_4& &&& &&b_4b_2\;b_3b_3\;b_2b_4& \\ && &&& &&b_4b_3\;b_3b_4& &&& &&b_4b_3\;b_3b_4& \\ && &&& &&b_4b_4& &&& &&b_4b_4& \end{eqnarray}
畳み込みというものを聞きました
畳み込み Wikipedia
\begin{eqnarray} (f*g)(m) &=& \sum_n f(n)g(m-n) \\ b_n &=& A_n\sum_{i=1}^{n} b_ib_{n+1-i} \end{eqnarray}
似てる
この式の$A_n$の部分を$2^n$に変えた、
\begin{eqnarray} b_n &=& 2^n\sum_{i=1}^{n} b_ib_{n+1-i} \end{eqnarray}
というものについて、
\begin{eqnarray} b_n = 1,2,16,288,10240,700416,92864512,24184487936,12484798840832,12835745584644096,\cdots \end{eqnarray}
これについてはOEIS( The On-Line Encyclopedia of Integer Sequences )
に載っていました。
A254744
↑これです。
どうやらカタラン数に関係するっぽいですね
\begin{eqnarray} c_n = \frac{(2n)!}{(n+1)!n!} = \frac{1}{n+1}\binom{2n}{n} \end{eqnarray}
この数には重要な漸化式があります。
\begin{eqnarray} c_0 &=& 1 \\ c_{n+1} &=& \sum_{i=0}^n c_ic_{n-i} \end{eqnarray}
ああ！畳み込んでますね！
じゃぁちょっと待ってください、私たちは$k=0,1$の場合の数列を何か特定しましたけど、それは何だったのでしょうか？
\begin{eqnarray} k&=&0\text{ の時} \\ A_t &=& \frac{1}{2^{t(k+1)}-2^{k+1}} \\&=& \frac{1}{2^{t}-2} \\ &\downarrow&\\ b_n &=& \frac{1}{2^n-2}\sum_{i=1}^{n} b_ib_{n+1-i} \\ \\ k&=&1\text{ の時} \\ A_t &=& \frac{1}{2^{2t}-2^2} \\ &=& \frac{1}{4^t-4} \\ &\downarrow&\\ b_n &=& \frac{1}{4^n-4}\sum_{i=0}^n b_ib_{n+1-i} \end{eqnarray}
何でこれだけ解けたんでしょうか...
色々調べたのですが、あらゆる$k$に対してこの数列$b_n$の$4$番目の項$b_4$をとってきて、その分数の分子を並べると$k=0$から順に
\begin{eqnarray}1,1,13,1,37,23,19,29,517,49,2053,1367,1171,607,32773,3121,131077,87383,74899,116509,2097157,\cdots \end{eqnarray}
となります。この数列自体はOEISには載っていないですが、これを二進数表記したとき、
\begin{eqnarray} &&1\\ &&1\\ &&1101\\ &&1\\ &&100101\\ &&10111\\ &&10011\\ &&11101\\ &&1000000101\\ &&110001\\ &&100000000101\\ &&10101010111\\ &&10010010011\\ &&1001011111\\ &&1000000000000101\\ &&110000110001\\ &&100000000000000101\\ &&10101010101010111\\ &&10010010010010011\\ &&11100011100011101\\ &&1000000000000000000101\\ &&110000110000110001\\ &&100000000000000000000101\\ &&10101010101010101010111\\ &&10010010010010010010011\\ &&11100011100011100011101\\ &&1000000000000000000000000101\\ &&110000110000110000110001\\ &&100000000000000000000000000101\\ &&10101010101010101010101010111\\ &&10010010010010010010010010011\\ &&1001011110110100001001011111\\ &&1000000000000000000000000000000101\\ &&110000110000110000110000110001\\ &&100000000000000000000000000000000101\\ &&10101010101010101010101010101010111\\ &&10010010010010010010010010010010011\\ &&11100011100011100011100011100011101\\ &&1000000000000000000000000000000000000101\\ &&110000110000110000110000110000110001\\ &&100000000000000000000000000000000000000101\\ \end{eqnarray}
となります。よく見るとパターンがあるので、色分けしましょう
\begin{eqnarray} && 0 : 1 \\ && 1 : 1 \\ && 2 : 1101 \\ && 3 : 1 \\ &&\color{red} 4 : 100101 \\ && 5 : 10111 \\ && 6 : 10011 \\ && 7 : 11101 \\ &&\color{red} 8 : 1000000101 \\ &&\color{purple} 9 : 110001 \\ &&\color{red} 10 : 100000000101 \\ &&\color{green} 11 : 10101010111 \\ &&\color{blue} 12 : 10010010011 \\ && 13 : 1001011111 \\ &&\color{red} 14 : 1000000000000101 \\ &&\color{purple} 15 : 110000110001 \\ &&\color{red} 16 : 100000000000000101 \\ &&\color{green} 17 : 10101010101010111 \\ &&\color{blue} 18 : 10010010010010011 \\ &&\color{orange} 19 : 11100011100011101 \\ &&\color{red} 20 : 1000000000000000000101 \\ &&\color{purple} 21 : 110000110000110001 \\ &&\color{red} 22 : 100000000000000000000101 \\ &&\color{green} 23 : 10101010101010101010111 \\ &&\color{blue} 24 : 10010010010010010010011 \\ &&\color{orange} 25 : 11100011100011100011101 \\ &&\color{red} 26 : 1000000000000000000000000101 \\ &&\color{purple} 27 : 110000110000110000110001 \\ &&\color{red} 28 : 100000000000000000000000000101 \\ &&\color{green} 29 : 10101010101010101010101010111 \\ &&\color{blue} 30 : 10010010010010010010010010011 \\ && 31 : 1001011110110100001001011111 \\ &&\color{red} 32 : 1000000000000000000000000000000101 \\ &&\color{purple} 33 : 110000110000110000110000110001 \\ &&\color{red} 34 : 100000000000000000000000000000000101 \\ &&\color{green} 35 : 10101010101010101010101010101010111 \\ &&\color{blue} 36 : 10010010010010010010010010010010011 \\ &&\color{orange} 37 : 11100011100011100011100011100011101 \\ &&\color{red} 38 : 1000000000000000000000000000000000000101 \\ &&\color{purple} 39 : 110000110000110000110000110000110001 \\ &&\color{red} 40 : 100000000000000000000000000000000000000101 \\ \end{eqnarray}
はい、先頭が"10000"か"10101"か"11000"か"11100"か"10010"とかで分けてみました。
これ以外は黒になっています。よく見ると$18$周期です。
\begin{eqnarray} && 0&& 1&& 2&& 3&& 4&& 5&& 6&& 7&&\color{red} 8&& 9&&\color{red} 10&&\color{green} 11&&\color{blue} 12&& 13&&\color{red} 14&&\color{purple} 15&&\color{red} 16&&\color{green} 17\\ &&\color{blue} 18&&\color{orange} 19&&\color{red} 20&&\color{purple} 21&&\color{red} 22&&\color{green} 23&&\color{blue} 24&&\color{orange} 25&&\color{red} 26&&\color{purple} 27&&\color{red} 28&&\color{green} 29&&\color{blue} 30&& 31&&\color{red} 32&&\color{purple} 33&&\color{red} 34&&\color{green} 35\\ &&\color{blue} 36&&\color{orange} 37&&\color{red} 38&&\color{purple} 39&&\color{red} 40 \end{eqnarray}
もうちょっと書いてみます。
\begin{eqnarray} &&& 0&&& 1&&& 2&&& 3&&&\color{red} 4&&& 5&&& 6&&& 7&&&\color{red} 8&&&\color{purple} 9&&&\color{red} 10&&&\color{green} 11&&&\color{blue} 12&&& 13&&&\color{red} 14&&&\color{purple} 15&&&\color{red} 16&&&\color{green} 17\\ &&&\color{blue} 18&&&\color{orange} 19&&&\color{red} 20&&&\color{purple} 21&&&\color{red} 22&&&\color{green} 23&&&\color{blue} 24&&&\color{orange} 25&&&\color{red} 26&&&\color{purple} 27&&&\color{red} 28&&&\color{green} 29&&&\color{blue} 30&&& 31&&&\color{red} 32&&&\color{purple} 33&&&\color{red} 34&&&\color{green} 35\\ &&&\color{blue} 36&&&\color{orange} 37&&&\color{red} 38&&&\color{purple} 39&&&\color{red} 40&&&\color{green} 41&&&\color{blue} 42&&&\color{orange} 43&&&\color{red} 44&&&\color{purple} 45&&&\color{red} 46&&&\color{green} 47&&&\color{blue} 48&&& 49&&&\color{red} 50&&&\color{purple} 51&&&\color{red} 52&&&\color{green} 53\\ &&&\color{blue} 54&&&\color{orange} 55&&&\color{red} 56&&&\color{purple} 57&&&\color{red} 58&&&\color{green} 59&&&\color{blue} 60&&&\color{orange} 61&&&\color{red} 62&&&\color{purple} 63&&&\color{red} 64&&&\color{green} 65&&&\color{blue} 66&&& 67&&&\color{red} 68&&&\color{purple} 69&&&\color{red} 70&&&\color{green} 71\\ &&&\color{blue} 72&&&\color{orange} 73&&&\color{red} 74&&&\color{purple} 75&&&\color{red} 76&&&\color{green} 77&&&\color{blue} 78&&&\color{orange} 79&&&\color{red} 80&&&\color{purple} 81&&&\color{red} 82&&&\color{green} 83&&&\color{blue} 84&&& 85&&&\color{red} 86&&&\color{purple} 87&&&\color{red} 88&&&\color{green} 89\\ &&&\color{blue} 90&&&\color{orange} 91&&&\color{red} 92&&&\color{purple} 93&&&\color{red} 94&&&\color{green} 95&&&\color{blue} 96&&&\color{orange} 97&&&\color{red} 98&&&\color{purple} 99&&&\color{red}100&&&\color{green}101&&&\color{blue}102&&&103&&&\color{red}104&&&\color{purple}105&&&\color{red}106&&&\color{green}107\\ &&&\color{blue}108&&&\color{orange}109&&&\color{red}110&&&\color{purple}111&&&\color{red}112&&&\color{green}113&&&\color{blue}114&&&\color{orange}115&&&\color{red}116&&&\color{purple}117&&&\color{red}118&&&\color{green}119&&&\color{blue}120&&&121&&&\color{red}122&&&\color{purple}123&&&\color{red}124&&&\color{green}125\\ &&&\color{blue}126&&&\color{orange}127&&&\color{red}128&&&\color{purple}129&&&\color{red}130&&&\color{green}131&&&\color{blue}132&&&\color{orange}133&&&\color{red}134&&&\color{purple}135&&&\color{red}136&&&\color{green}137&&&\color{blue}138&&&139&&&\color{red}140&&&\color{purple}141&&&\color{red}142&&&\color{green}143\\ &&&\color{blue}144&&&\color{orange}145&&&\color{red}146&&&\color{purple}147&&&\color{red}148&&&\color{green}149&&&\color{blue}150&&&\color{orange}151&&&\color{red}152&&&\color{purple}153&&&\color{red}154&&&\color{green}155&&&\color{blue}156&&&157&&&\color{red}158&&&\color{purple}159&&&\color{red}160&&&\color{green}161\\ &&&\color{blue}162&&&\color{orange}163&&&\color{red}164&&&\color{purple}165&&&\color{red}166&&&\color{green}167&&&\color{blue}168&&&\color{orange}169&&&\color{red}170&&&\color{purple}171&&&\color{red}172&&&\color{green}173&&&\color{blue}174&&&175&&&\color{red}176&&&\color{purple}177&&&\color{red}178&&&\color{green}179\\ &&&\color{blue}180&&&\color{orange}181&&&\color{red}182&&&\color{purple}183&&&\color{red}184&&&\color{green}185&&&\color{blue}186&&&\color{orange}187&&&\color{red}188&&&\color{purple}189&&&\color{red}190&&&\color{green}191&&&\color{blue}192&&&193&&&\color{red}194&&&\color{purple}195&&&\color{red}196&&&\color{green}197\\ &&&\color{blue}198&&&\color{orange}199&&&\color{red}200 \end{eqnarray}
うん、綺麗だね。
ちなみにこの黒いところはOEISに$18n-5$として載っていると思ったのですがどうやら
https://oeis.org/A063305
しかないようです。
$\text{Dimension of the space }S_n^{\text{new}}(\text{Gamma}_1(32))\text{ of weight $n$ cuspidal newforms for Gamma}_1( 32 ).$
かっこいいですね。
ん無理！
無理でした。
別の方向アルヨ
そうです。普通に微分方程式と考えて解いてもいいはずです。
\begin{eqnarray}
f'(2x) &=& f'(x)f(x) \\
2f'(2x) &=& 2f'(x)f(x)
\end{eqnarray}ここで、
\begin{eqnarray} \frac{d}{dx}f\qty(x)^2 &=& 2f(x)f'(x) \\ \frac{d}{dx}f\qty(2x) &=& 2f'(2x) \\ \end{eqnarray}
なのでちょうど
\begin{eqnarray} 2f'(2x) &=& 2f'(x)f(x) \\ \frac{d}{dx}f\qty(2x) &=& \frac{d}{dx}f\qty(x)^2 \end{eqnarray}
同値かどうか疑問がありますが、こうできそうです。
\begin{eqnarray} 2f'(2x) &=& 2f'(x)f(x) \\ \frac{d}{dx}f\qty(2x) &=& \frac{d}{dx}f\qty(x)^2 \\ f(2x) &=& f(x)^2 + C \end{eqnarray}
え？これ解けるの？
関数方程式界隈の皆さん解いてください
$x=0$を入れると
\begin{eqnarray} f(0) &=& f(0)^2+C \\ f(0)^2 - f(0) + C &=& 0 \\ f(0) &=& \frac{1}{2}\qty(1\pm\sqrt{1-4C}) \end{eqnarray}
さっき上の方で$a_0=2^k$と分かっていたので
\begin{eqnarray} 2^k - 2^{2k} &=& C \end{eqnarray}
$k=0$だと$C=0$でこれは$f(x)=e^{tx}$にあたり、
$k=1$だと$C=-2$でこれは$f(x)=2\cosh(\sqrt{t}x)=e^{-\sqrt{t} x} + e^{\sqrt{t} x}$に当たります。
実際、
\begin{eqnarray} f(2x)-f(x)^2 &=& e^{-2\sqrt{t} x} + e^{2\sqrt{t} x} - \qty(e^{-\sqrt{t} x} + e^{\sqrt{t} x})^2 \\&=& e^{-2\sqrt{t} x} + e^{2\sqrt{t} x}-\qty(e^{-2\sqrt{t}x}+2+e^{2\sqrt{t}x}) \\&=& -2 \end{eqnarray}
となりますね！
$f'(2x) = f'(x)f(x) $なので$x=0$を入れると
$f'(0) = f'(0)f(0)$
うーんなんかさっきの議論と同じものをたどりそうですね。
\begin{eqnarray} \frac{d}{dx}f\qty(x)^2 &=& 2f(x)f'(x) \\ \frac{d}{dx}f\qty(2x) &=& 2f'(2x) \\ \end{eqnarray}
なのでちょうど
\begin{eqnarray} 2f'(2x) &=& 2f'(x)f(x) \\ \frac{d}{dx}f\qty(2x) &=& \frac{d}{dx}f\qty(x)^2 \end{eqnarray}
同値かどうか疑問がありますが、こうできそうです。
\begin{eqnarray} 2f'(2x) &=& 2f'(x)f(x) \\ \frac{d}{dx}f\qty(2x) &=& \frac{d}{dx}f\qty(x)^2 \\ f(2x) &=& f(x)^2 + C \end{eqnarray}
え？これ解けるの？
関数方程式界隈の皆さん解いてください
$x=0$を入れると
\begin{eqnarray} f(0) &=& f(0)^2+C \\ f(0)^2 - f(0) + C &=& 0 \\ f(0) &=& \frac{1}{2}\qty(1\pm\sqrt{1-4C}) \end{eqnarray}
さっき上の方で$a_0=2^k$と分かっていたので
\begin{eqnarray} 2^k - 2^{2k} &=& C \end{eqnarray}
$k=0$だと$C=0$でこれは$f(x)=e^{tx}$にあたり、
$k=1$だと$C=-2$でこれは$f(x)=2\cosh(\sqrt{t}x)=e^{-\sqrt{t} x} + e^{\sqrt{t} x}$に当たります。
実際、
\begin{eqnarray} f(2x)-f(x)^2 &=& e^{-2\sqrt{t} x} + e^{2\sqrt{t} x} - \qty(e^{-\sqrt{t} x} + e^{\sqrt{t} x})^2 \\&=& e^{-2\sqrt{t} x} + e^{2\sqrt{t} x}-\qty(e^{-2\sqrt{t}x}+2+e^{2\sqrt{t}x}) \\&=& -2 \end{eqnarray}
となりますね！
$f'(2x) = f'(x)f(x) $なので$x=0$を入れると
$f'(0) = f'(0)f(0)$
うーんなんかさっきの議論と同じものをたどりそうですね。
他
他なんですが、普通に数値計算して値を出してみました。($k=2$の場合)
https://www.desmos.com/calculator/brvbdycweh
まぁすぐに値が小さくなって全然見えないんですけどね。
これをいじっていてとんでもないことに気づいたのです。
とりあえず、$k=2$からおかしくなるので$k=2$の時を執拗に遊んでいたんですね。
まぁ無限(有限だろ)にいろんな面白そうな数列を出してはOEISで調べて全部無いを繰り返して、具体的に関数を求めたりもしたんですが、
\begin{eqnarray}
3n\cdot\frac{a_{3n}a_{3n}}{a_{3n-3}a_{3n+3}}
\end{eqnarray}
という数列を考えてみました。($k=2$では$n$が$3$の倍数じゃないときは$a_n$は$0$になってしまうのでこうしています。)
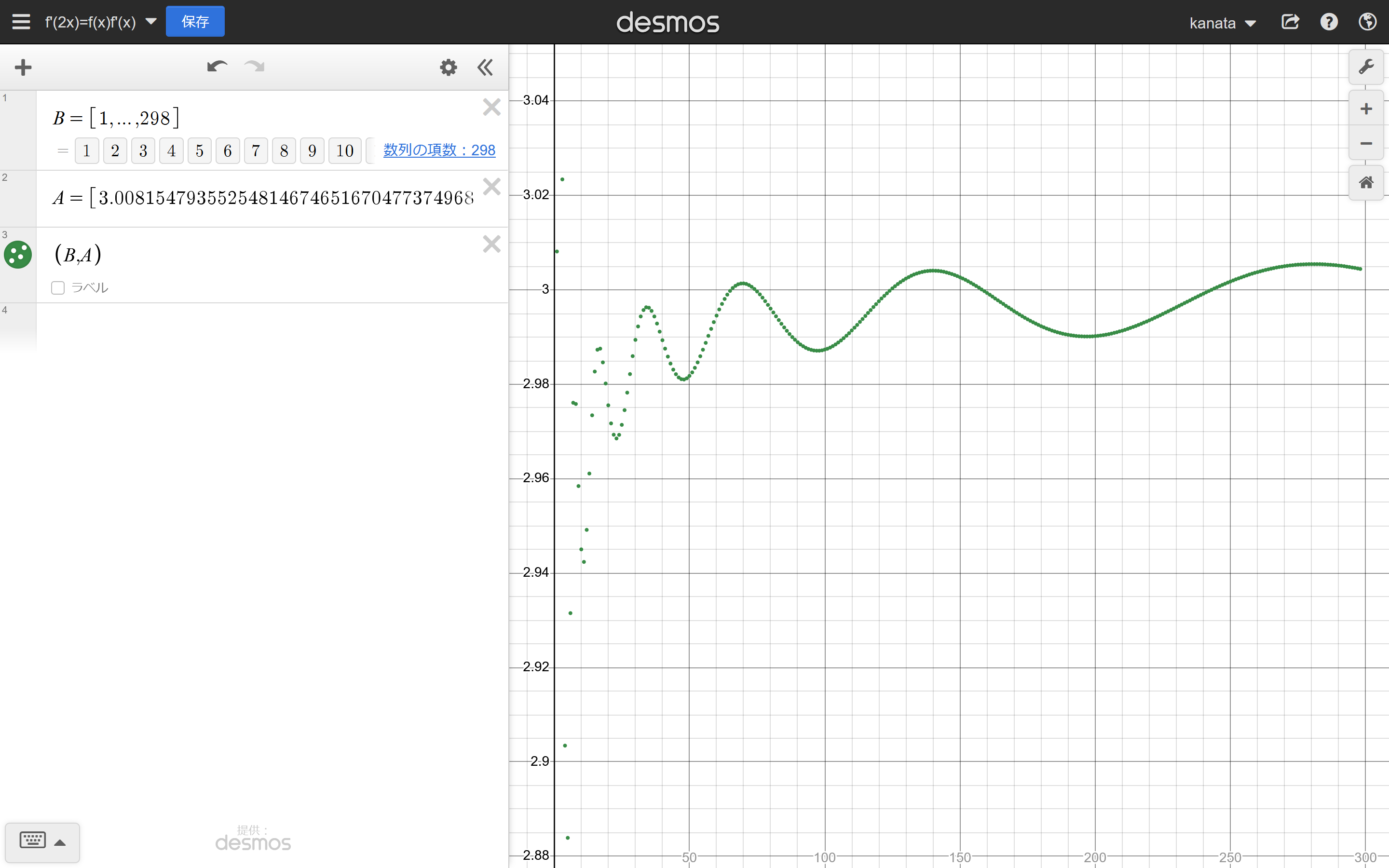
このプロットがこうです。
えーー
何と振動しています。
別に精度が悪いとかではなくて滑らかに振動しています。
さすがにきもいですね。
$k=0$と$k=1$も$k=3$もやってみましょう
![!FORMULA[235][36494538][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FLBImQFmzkRhVThN5imHU.png?alt=media)
$k=0$
![!FORMULA[236][36494569][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FryMwsAsJx7TGlNy0uL8x.png?alt=media)
$k=1$
![!FORMULA[237][36494631][0]](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2Fo5nM10dVsnTSj7RPoosy.png?alt=media)
$k=3$
$k=3$についてはなんかこう対数的な何かが見えたので頑張って近似しました
https://www.desmos.com/calculator/ojjwamkomn
そしてほかの$k$も表示
![!FORMULA[240][36494662][0]が紫 !FORMULA[241][36494693][0]が黒 !FORMULA[242][36494724][0]が緑](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FZRX7IiumrYzP6pgJaoVg.png?alt=media)
$k=4$が紫 $k=5$が黒 $k=6$が緑
ぐにゃぐにゃする
ぐにゃぐにゃすることについては、非常に興味深く、そしてこの問題の解決をさせてくれない要因になっています。
だって$k=0,1$ではならないんだもん。
単調ではない関数であるということが分かりますね。
上の図から振幅はわからないですが、周期については$\sin(9\ln(x))$とほぼ同じものであると分かります。
それだけ。
お わ り
投稿日：12日前
更新日：12日前
この記事を高評価した人
この記事を高評価した人
高評価したユーザはいません
この記事に送られたバッジ
この記事に送られたバッジ
バッジはありません。
投稿者
投稿者
コメント
コメント
他の人のコメント
コメントはありません。
読み込み中...
読み込み中