連続型の確率変数はどうして積分を使うの？

統計学を学習するとある時突然積分に出くわすかと思います。

本稿はなんで積分が出てくるのか私なりに分かりやすく解説したつもりの記事です。
数学に馴染みのない方や苦手意識を抱えている方にも理解いただけるよう作成したつもりなので多くの方の参考になれば幸いです。

構成

第一章

まずは確率とは何だったか統計学で出てくる用語も軽く触れつつまとめていく。また、この後の章で必要になる集合や変数についての考えも軽く触れておく。

第二章

ここでは積分の定義について、関数とは何だったか振り返りつつ高校で学んだ内容と大学の講義で出てくる内容を確認していく。

第三章

二部で見た積分の定義を踏まえ、確率(連続型確率変数)でなぜ積分が使われるか深ぼりしていく。

また、本稿では添え字(文字列)を表記する際は[]を使ってa i と表し、関数についてはf(x)のように()を使って表記する。

第一章

まず、確率とは何か考えてみる。
確率の概略をお伝えすると「ある事象の現れやすさ」である。
ここで出てきた「事象」、「現れやすさ」についてもう少し詳しく考えていこう。

「事象」(=起こった事実)は何か行動を起こして発生するのであって、この”行動”の事を数学用語で「試行」と呼び、さらに、この試行によりあらわれた結果を「事象」と呼んでいる。
例えばトランプ52枚から1枚めくる試行の結果として「エース」(=”条件A”)が出た場合、結果に当てはまるのは”ハートのエース”、”ダイヤのエース”、”ミツバのエース”、”クローバーのエース”の4つである。
一方で、結果として「ダイヤのエース」(=”条件B”)が出たと言った場合、事象は1つである。

注目した”条件X”を満たす結果が複数あればその事象Xは「現れやすい」と考えて、

(注目した”条件X”を満たし得る結果の数)/(試行により起こり得るすべての結果の数)

を事象Xの起こる確率の数学的な定義とするのである。

この「試行Aにより起こり得るすべての結果の数」は、試行Aにより起こるという条件をもつ集合の中に、その条件を満たす結果(=集合の要素)が複数あるとも考えられる。

「同様に確からしい」とは…

事象が一つの場合(これを根元事象とも言う)、外的な要因なく表れやすさは変わらないことを「同様に確からしい」と呼ぶ。
例えば、たまたまめくった1枚が2枚くっついてしまっていた場合、得られる確率が変わってしまう。サイコロを振る試行でももし角が欠けていたりしてある目が出やすくなっているといった場合は正しい確率を得たとは言えない。

積事象と互いに排反であること

事象Aと事象Bが同時に起こることをA∩Bと表し、積事象と呼ぶ。
一方、トランプを1枚めくる試行についてスペードが出る事象Aとハートが出る事象Bを考えた時、AとBは同時に起こらない(※注1)。
このように同時に起こらない事象については事象AとBは互いに排反であるという。
事象AとBが互いに排反である時、積事象の確率P(A∩B)はもちろん0である。
(※注1)極端な話、もしハートとスペードの絵柄が入った全く新しいトランプの絵札が4枚加わった場合、事象AとBは排反ではなくなる。

和事象の確率と集合の考え

事象Aまたは事象Bが起こる確率を和事象と呼びP(A∪B)で表す。
ある試行により起こり得るすべての結果を集めた集合Ωと、その中の事象A(=注目した”条件A”を満たし得る結果の集合)、事象B(=注目した”条件B”を満たし得る結果の集合)に対して、確率の定義からP(A∪B)=｜A∪B｜/｜Ω｜と書ける。
(ただし、｜＊｜は集合＊の要素の数を表している。)
ここで、｜A∪B｜は事象A∪Bの結果の総数を表しているのだが、単純に事象Aの結果の総数と事象Bの要素の結果の総数を足すと、AとBで共通している結果の総数(A∩B)を2回足し合わせることになるので｜A∪B｜=｜A｜+｜B｜－｜A∩B｜が成り立つことに注意せよ。
従って、P(A∪B)= ｜A∪B｜/｜Ω｜=｜A｜/｜Ω｜+｜B｜/｜Ω｜－｜A∩B｜/
｜Ω｜=P(A)+P(B)－P (A∩B)が成り立つ。
もし、事象AとBが互いに排反であればP(A∪B)=P(A)+P(B)である。

次に、これまで説明してきた内容をもとに (離散型)確率変数の考えと累積分布関数を紹介しておく。
まず、ある事象Aにおける複数の結果をa[1],a[2], … ,a[n]と表せば、事象Aは集合としてA={a[1],a[2], … ,a[n]}と書ける。
この時、”変数”という考えが出来る。
すなわち、a[1],a[2], … ,a[n]の内、いずれかa i を取る、といった考えである。
この、X= a i の事を確率変数と呼ぶ。
特にサイコロの目を考えた場合、サイコロの目={1, 2, … ,6}であり、X= a i と表せるが、このように変数が飛び飛びの値を取る場合を特に離散型確率変数と呼ぶ。

累積分布(離散型(※注2))

確率変数Xがある値a,bに対してa≦X≦bを取るときの確率P(a≦X≦b)を累積分布関数という。
(※注2)後に紹介する連続型確率変数の場合も累積分布関数と呼ぶがここでは理解のため敢えて離散型と強調しておく。
累積分布の考えをまたサイコロの目を例に考えてみる。
サイコロを1回振った時の出た目Xが2≦X≦5を取るときの確率P(2≦X≦5)とはサイコロの目がX=2か3か4か5である確率ということである。
つまり、これらを事象A2, A3, A4, A5と書き改めるとP(2≦X≦5)=P(A2∪A3∪A4∪A5)が成り立つ。
今事象は互いに排反なので、
P(2≦X≦5)=P(A2∪A3∪A4∪A5)= P(A2)+P(A3)+P(A4)+P(A5)=4/6=2/3となる。
a=z[1]≦z[2]≦…≦z[n]=bとした時、各結果z[i]が相異なるもの(z[i]≠z[j], i,j∈｛1,2,…,n｝)であれば、同時に起こること(X= z[i]かつX=z[j])はあり得ないので互いに排反であると言えてP(a≦X≦b)= P(X=z[1])+ P(X=z[2])+…+ P(X=z[n]) =∑_[i=1→n]P(X=z[i])
が成り立つ。

開区間・閉区間について

{x｜a≦x≦b}という集合を特に閉区間と呼び[a, b]と表す。
{x｜a<x<b}という集合を特に開区間と呼び(a, b)と表す。

第二章

第一章とは打って変わって積分について振り返る。その前に、まずは関数の定義についておさらいしておく。

関数とは

中学・高校に入るとaとかx、yといった文字が出てくるようになる。そして、”変数”という考えをもとにxの値が増えるにつれてyがどうなるのかグラフを作成してみるといった経験をしたと思う。
実際、直線グラフは一般的にy=ax+b(a,b:定数)と書けて、おわん型のグラフはy=ax^2+bx+c(a,b,c:定数)と書けた。このような変数xとyの関係式を関数と呼んだのだが、もう少し踏み込むと「何か値を入れたら値が一つだけ返ってくる」ものである。
何が言いたいかというと、xにある値aを入れたらyの値が複数出てきたというものは関数とは呼ばないということである。
例えば、放物線y=3x^2はx=2の時y=12と一つの値に定まるが、
円の方程式x^2+y^2=5についてはx=2の時y=-1, 1となるのでこれは厳密には関数とは言わないのである。
以上を踏まえて関数については、xにある値を入れた時「yが唯一つ定まる」ものと表現することができる。
本稿では定義域、値域ともに実数全体とした対応関係を関数と呼ぶ。

積分ってなんだっけ

積分と聞くとパッと浮かぶのは「微分の逆」というイメージではないだろうか。もちろん、このイメージは正しい。しかし、もう少し進むと積分はある関数とx軸とを囲む面積であるという事も並行して教わる。特にテスト勉強や受験で使うだけの場合、そういうものだと頭に叩き込んで対処してきた方も多いのではないかと思う。かく言う私も当時はその一人だった。
ただ、ここで立ち止まって考えてみると「何で微分の逆の操作をすると面積が求まるの？」という疑問が出てくるだろう。
この疑問については順番を入れ替えて見ることで道筋が見えてくるかと考える。どういうことか、まずは高校の数Ⅲもしくは大学1年次に出てくる積分(定積分)の定義を見てみよう。
そのために、以下に必要なワード3つ書き並べた。
かなり堅苦しく感じられるかもしれないが、捕捉しつつなるべく分かりやすく解説していく。

分割

任意の閉区間[a, b]について、a=x[0]<x[1]<x[2]<…<x[n]=bを満たす要素の集合｛x[0], x[1], x[2], …,x[n]｝を閉区間[a, b]の分割という。また、特に分割Δ=｛x[0], x[1], x[2], …,x[n]｝の要素x i を閉区間[a, b]の分点という。

中間値集合

閉区間[a, b]の分割Δ=｛x[0], x[1], x[2], …,x[n]｝に対して、各閉区間[x[i-1], x[i]]⊂[a, b]から1つw[i]を取り集めた｛w[0], w[1], w[2], …, w[k]｝をΔに付随する中間値集合という。

ダルブー和

閉区間[a, b]の分割Δ=｛x[0], x[1], x[2], …,x[n]｝とそれに付随する中間値集合Γ=｛w[0], w[1], w[2], …, w[n]｝に対して、ある関数f(x)における総和∑_[i=1→n]f(w[i])(x[i]-x[i-1])をダルブー和といい、S(Δ,Γ)で表す。

(※各横の長さは一定ではなく長いものから短いものまで様々である。)

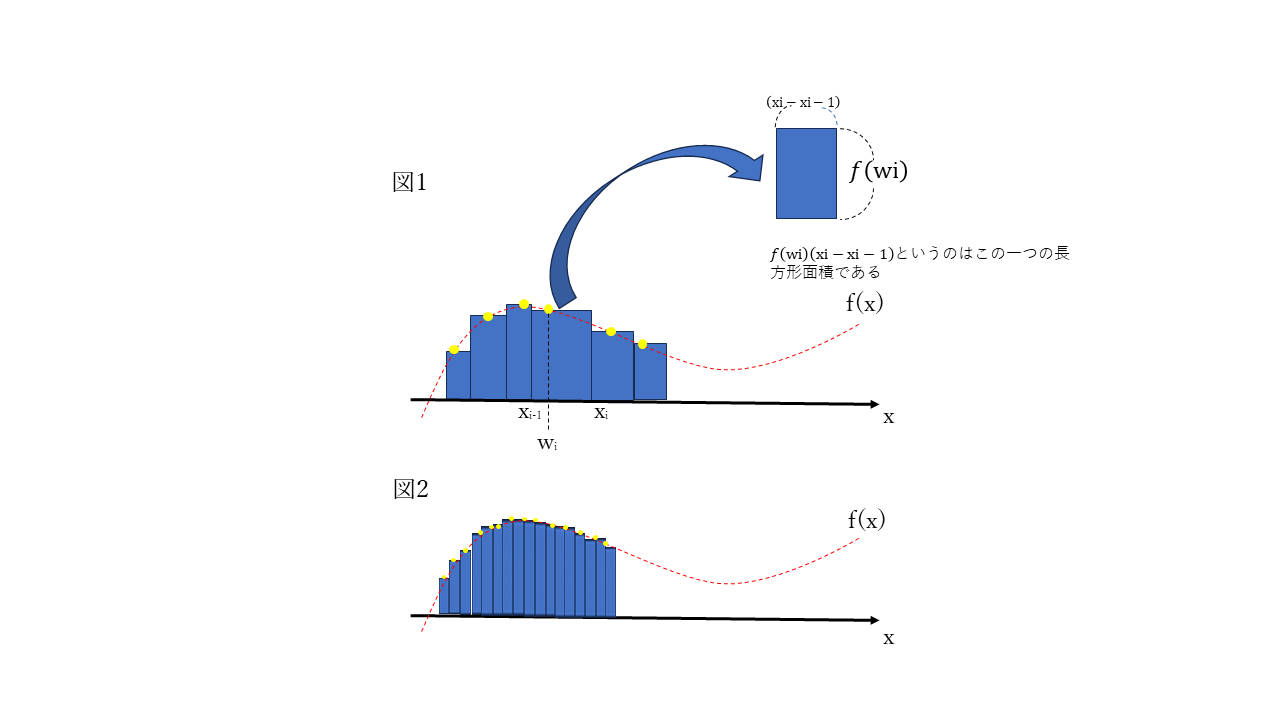イメージ図

定積分

閉区間[a, b]の分割Δ=｛x[0], x[1], x[2], …,x[n]｝とそれに付随する中間値集合Γ=｛w[0], w[1], w[2], …, w[n]｝に対して、任意の正数εとある正数δによりmax｛x[1]- x[0], x[2]- x[1],…, x[n]-x[n-1]｝<δならば｜S-S(Δ,Γ)｜<εを満たすSが存在するとき、このSを関数f(x)のaからbまでの定積分といい、∫[a→b]f(x)dxで表す。
定積分ではx[i]-x[i-1] (横の長さ)をより小さくした時のダルブー和に近い値Sを定義している。
定義の記号についてもう少し詳しく見ていこう。
max｛x[1]- x[0], x[2]- x[1],…, x[n]-x[n-1]｝<δというのは一番大きいx[i]-x[i-1] (横の長さ)がある小さい値δよりも小さいという事である。
つまり全てのx[i]-x[i-1] (横の長さ)が短くなっているという条件の下で、定積分Sは｜S-S(Δ,Γ)｜<εを満たすものであるという事である。
｜S-S(Δ,Γ)｜<εというのはS-S(Δ,Γ)が0に近い、差が殆どないということを表している。εというのは正数であれば何でも良い値なので、逆に言えばどんな小さい値でもこの不等式が成り立っていると考えるのである。
この定義を基にいくつかの定理を導出した後、定積分というのは微分の逆の操作から算出できるという定理(微積分学の基本定理)が証明されるのだが、本稿では証明については割愛する。

第三章

次の確率を考えてみようと思う。

「マッチングアプリで知り合った人と実際に会うとなった時に、来る相手の身長がプロフィール通りちょうど182cmである確率Pは？」

日本語としては恐らく違和感ない文章かと思われる。
しかし、数学的に"ちょうど"という言葉に注目して見ると、極端な話、「身長が182.0000…cmの人が来る」というのはいかがなものだろうか。
この事をもう少し深掘りしていくと、
身長や体重、或いは距離や時間などといった概念は連続しており、小数点以下も何ミリ、何マイクロ、…とさらに細かく数値が刻まれている。
「身長が182cmの人が来る」というのは小数点以下がすべて0であるということであるが、
現実世界で小数点以下第n位すべての値を正確に測定するのは不可能である故に小数点以下第n位すべて0であると保証することは出来ないと考えるべきである。
従って、冒頭の文章は現実世界で数学的に検証するのであれば修正が必要であり、

「マッチングアプリで知り合った人と実際に会うとなった時に、来る相手の身長がプロフィール通りちょうど181cm以上、183cm未満である確率Pは？」

というように、”範囲”をもって表現すると自然である。
以降、より数学的に文章を変換していく。
範囲を閉区間[a, b]で表す。
さらに、a～bまでの範囲を細かく区切ってa=t[1]≦t[2]≦…≦t[n]=bとする。
つまり、[t[i-1], t[i]]は[a, b]の中のさらに細かい範囲である。
(※この範囲[t[i-1], t[i]]の幅は一定ではないものとする。)
各小範囲[t[i-1], t[i]]における確率はそれぞれ異なる。
今回であれば、181cm近辺または183cm近辺は来る確率が低く、182cm周辺で来る確率が高くなることが想定できる。
より範囲を細分化してみると、181cm近辺または183cm近辺の各小範囲[t[i-1], t[i]]はそれぞれ近しい確率をとり、また182cm周辺の各小範囲[t[i-1], t[i]]もそれぞれ近しい確率を取ると考えられる。
いま、各[t[i-1], t[i]]における確率をp[t[i]]とおく。さらに細かい期間をt[i-1]=λ[0]≦λ[1]≦…≦λ[m]=t[i]と書くと、 [t[i-1], λ[ζ]]は比較的短い範囲なので
各確率p[λ[0]], p[λ[1]], …, p[λ[m]]は範囲が広がるに応じて高くなると(勝手に)仮定する。
すなわち、比例関係から
p[λ[1]]/ (λ[1]－t[i-1])= p[λ[2]] /(λ[2]－t[i-1])= … = p[λ[m]] /(λ[m]－t[i-1])
である。－(★)
ここで、関数f: [a, b]→ℝ、λ[ζ]→p[λ[ζ]] / (λ[ζ]－t[i-1])
(λ[ζ]は各[t[i-1], t[i]]⊂[a, b]に属する任意の元)
を定めると、上述の★において
f(λ[ζ])=p[λ[ζ]] / (λ[ζ]－t[i-1])
＝p[λ[1]]/ (λ[1]－t[i-1])= p[λ[2]] /(λ[2]－t[i-1])= … = p[λ[m]] /(λ[m]－t[i-1])= p[t[i]] /( t[i]－t[i-1])と書けるので
p[t[i]] =f(λ[ζ]) ×( t[i]－t[i-1])
が得られる。
各p[t[i]]は1≦i≦nにおける整数の場合分けなので、第一章で見た累積分布の考えから[a, b]全体の確率はΣp[t[i]]=Σf(λ[ζ])(t[i]－t[i-1])である。…(◇1)
最後に、★で述べた部分に戻る。
ここの考えはこちらで勝手に想定した仮定を前提にしている。
常に比例関係が成り立っているわけではないのである。
しかし、範囲[t[i-1], t[i]]がより短ければどうだろうか。
極端な話、範囲が一時点x=λ[ζ]∈[t[i-1], t[i]]のみの短さであれば比例関係も何もない。
正確には第三章の冒頭に述べたように一時点の確率(x=t[ζ]の確率)は考えられないが、すなわち、一点x=tζ∈[t[i-1], t[i]]のみの短さに"近づけ"れば仮定も自然に成り立つ。
この時全体の確率Σp[i]も求める"真"の確率Pに近づく。…(◇2)
従って、範囲[t[i-1], t[i]]の前提条件として短い範囲であることを加える必要がある。…(◇3)
長々と展開してきたが、以上◇1,2,3をまとめると数学的に以下のように書ける。
任意の正数εに対して、正数δがあり求める真の確率Pはmax{t[2]－t[1],t[3]－t[2],…,t[n]－t[n-1]}<δならば|P－Σf(λ[ζ])(t[i]－t[i-1])|<εを満たす。
これは第二章で見た積分の定義そのものである。
故に、区間[a,b]∋xにおいてP=∫[a→b]f(x)dxが成り立つ。

連続型確率変数

身長に限らず、体重、ものの面積や時間など連続的な値を範囲にとる場合の確率変数を連続型確率変数という。

連続型確率変数と累積分布関数

連続型の確率変数における確率を考える際には”範囲”が必要になることを見てきた。つまり、
a≦x≦bにおける確率Pというのが∫[a→b]f(x)dxである事を確認してきた訳だが、これは第一章で見た累積分布関数そのものでもある。
離散型の場合、確率の定義から試行により起こり得るすべての結果の集合をΩ=｛a[1],a[2],…,a[n]｝とすればa[1]≦X≦a[n]における確率というのは
P(a[1]≦x≦a[n])=P(X=a[1])+ P(X=a[2])+…+P(X=a[n])=｜Ω｜/｜Ω｜=1となる。
これは確率の性質とも言える部分であるが、では連続型の場合や要素数が無限にある場合はどうだろうか。
第三章冒頭の例でも見たように全体の集合の要素の数は必ずしも有限ではない。この場合、上述のように計算から全事象の確率が1であることを導くのは難しいため(※5)、予め1であると定義しておく必要がある。それが次に述べる規格化条件である。
((※5)｜∞｜/｜∞｜＝？？)

規格化条件

離散型及び連続型の確率変数において、試行により起こり得るすべての結果の集合の要素の数が無限にある場合、その全事象の確率が1であると定めることを規格化条件とよぶ。
つまり、確率論及び統計学ではこの規格化条件のもと、
∑_(i=1→∞)P(X=a[i])=1、
∫[-∞→∞]f(x)dx =1
が成り立っているのである。