正五角形の対角線の長さ

TV番組「3か月でマスターする数学」

毎週水曜日21:30からNHK Eテレで放送されている番組 「3か月でマスターする数学 - NHK」 を見ています。
大人の復習のために中学校・高校数学解説する番組で、レジェンド数学者の秋山仁先生が出演されていて毎週楽しみにしています。本編では数学に詳しい横山明日希さんやヨビノリたくみさんが（受講者の代表する役割の）塚原愛アナにわかりやすく説明するスタイルになっています。
放送前からテキスト
3か月でマスターする 数学 (NHKシリーズ)
3か月でマスターする 数学 (NHKシリーズ)
も売っていて読むとネタバレになりますが各回の放送前に予習することもできます。もちろん放送後に復習もできます。
text

（7月3日放送の）第2回平方根・無理数を見て

発見の歴史や、白銀比と呼ばれる（他の比をそう呼ぶ場合もあるそうですが）比$1:\sqrt{2}$が2等分しても縦横比が変わらない性質があるため、「紙のサイズ」に利用されているなどの話や秋山仁先生によるコーナー「JIN-JINの部屋」で黄金比$$1:\frac{1+ \sqrt{5} }{2} $$がいろいろなところに現れるというお話がありました。3枚の黄金比の長方形を組み合わせた立体の頂点を糸で結ぶと、正二十面体ができるなど、実に興味深く面白いお話でした。
そして、本編に戻りその黄金比が現れるものの一つ正五角形の対角線に関する問題が出題されました。

番組（とテキスト）では正五角形と対角線からなる図にうまく二等辺三角形を見つけて、等しい角を見つけて、対角線の長さを$x$と置いて、$x^2-2x-4=0$という式を導いて、
解の公式$x=\frac{-b \pm \sqrt{b^2-4ac} }{2a}$を使用して$x=1+\sqrt{5}$を求めていました。
もちろんこれでもよいのですが、ここまで図形の相似とかを使ってきたのに最後だけ、解の公式を適用するというのが少々唐突に感じました。
そこで、解の公式を使わずに説明できないかを考えました。
そして、一応解の公式は使わないでもできる説明を考えました。ただ若干「なんでそうするの？」と言われそうな部分もあるので、よりわかりやすい説明があればお教えいただきたいです。私もさらなる説明を考えてみようと思います。

正五角形の対角線の長さの自分なりの求め方

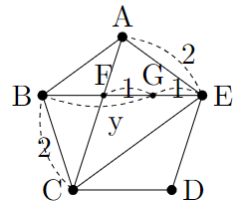正五角形と対角線
1辺の長さ2の正5角形ABCDEの対角線BEとACの交点をFとする。
五角形は三角形3つからなると言えるので、内角の和は540度で、それぞれの内角(例えば、∠BAE)は108度、△ABEはAB=AEの二等辺三角形なので、∠ABE=∠AEBで、三角形の内角の和180度なので、以降角度の単位の度を省略すると、
$$∠ABE=∠AEB=(180-108)÷2=36$$
△BCAは、△ABEを回転したものなので、$∠FAB=36$
$$∠AFE=∠FAB+∠ABF=72$$
$$∠FAE=∠BAE-∠FAB=108-36=72$$
なので、∠AFE=∠FAEより、△EAFはAE=FEとなる二等辺三角形。
$FE=AE=2$である。
FとEの中点をGとすると、$FG=GE=1$
$$y:=BG$$と置くと、
$$BE=y+1$$
$$BF=y-1$$
∠BEC=108-36-36=36であり、△BCEと△FBCは頂角がどちらも36度の二等辺三角形なので相似。
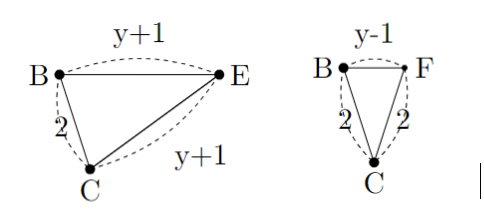相似の関係にある△BCEと△FBC
$$\frac{BE}{BC}=\frac{FC}{FB}$$
$$\frac{y+1}{2}=\frac{2}{y-1}$$
$$y^2-1=4$$
$$y^2=5$$
$$y=\sqrt{5} $$
$$BE=1+y=1+\sqrt{5}$$
よって対角線の長さは$1+\sqrt{5}$∎

中点GやBGをyと置くのが唐突と思われるかもしれませんが、「解の公式」は使わずに「正五角形の1辺の長さが2のとき、対角線の長さは1+√5」を示せました。
番組の第3回で秋山先生もおっしゃっていましたが「山を登るルートがいろいろあるのと同様に一つの定理の証明はもいろいろあるのが数学の面白い所」なので、各自いろいろな自分なりの証明を考えてみると、その面白さが感じられるのでお勧めです。問題の答えが1つで、それが分かった後でも別証明を考えて何度でも楽しめると思います。
繰り返しになりますが、「正五角形の1辺の長さが2のとき、対角線の長さは1+√5」のよりわかりやすく自然な説明があればぜひお教えいただきたいです。