積分　問題①

$$媒介変数tを用いて\begin{eqnarray} \left\{ \begin{array}{l} \ x=t^2 \\ \ y=t^3 \end{array} \right. \end{eqnarray}　と表現される曲線について考える。$$
$(1)曲線Cの0\leq t\leq1$の長さを求めよ。
$(2)曲線C上の点(1,1)における接線と曲線Cで囲まれた図形の面積を求めよ。$

(1)$x=f(t),y=g(t) と媒介変数表示された曲線の α≤t≤β の部分の長さは、$
$$\int_{α }^{β}\sqrt{f'(t)^2+g'(t)^2}dt\quad とあらわされる。$$
$(ただし、f(t),g(t)は微分可能で、f'(t),g'(t)は連続とする。)$
よって今回の曲線の長さは、
$$\int_{0}^{1}\sqrt{(2t)^2+(3t^2)^2}dt$$
$$=\int_{0}^{1}\sqrt{4t^2+9t^4}dt$$
$$=\int_{0}^{1}t\sqrt{4+9t^2}dt$$
$4+9t^2=uと置換する$
$$=\frac{1}{18}\int_{4}^{13}\sqrt{u}dt$$
$$=\frac{1}{27}(13\sqrt{13}-8)$$

(2)
曲線Cのグラフを書く
$x=t^2,y=t^3であるから、y^2=x^3$
$よってy=x\sqrt{x},y=-x \sqrt{x}の二つの関数を考えればよい。$
よってグラフを書くと

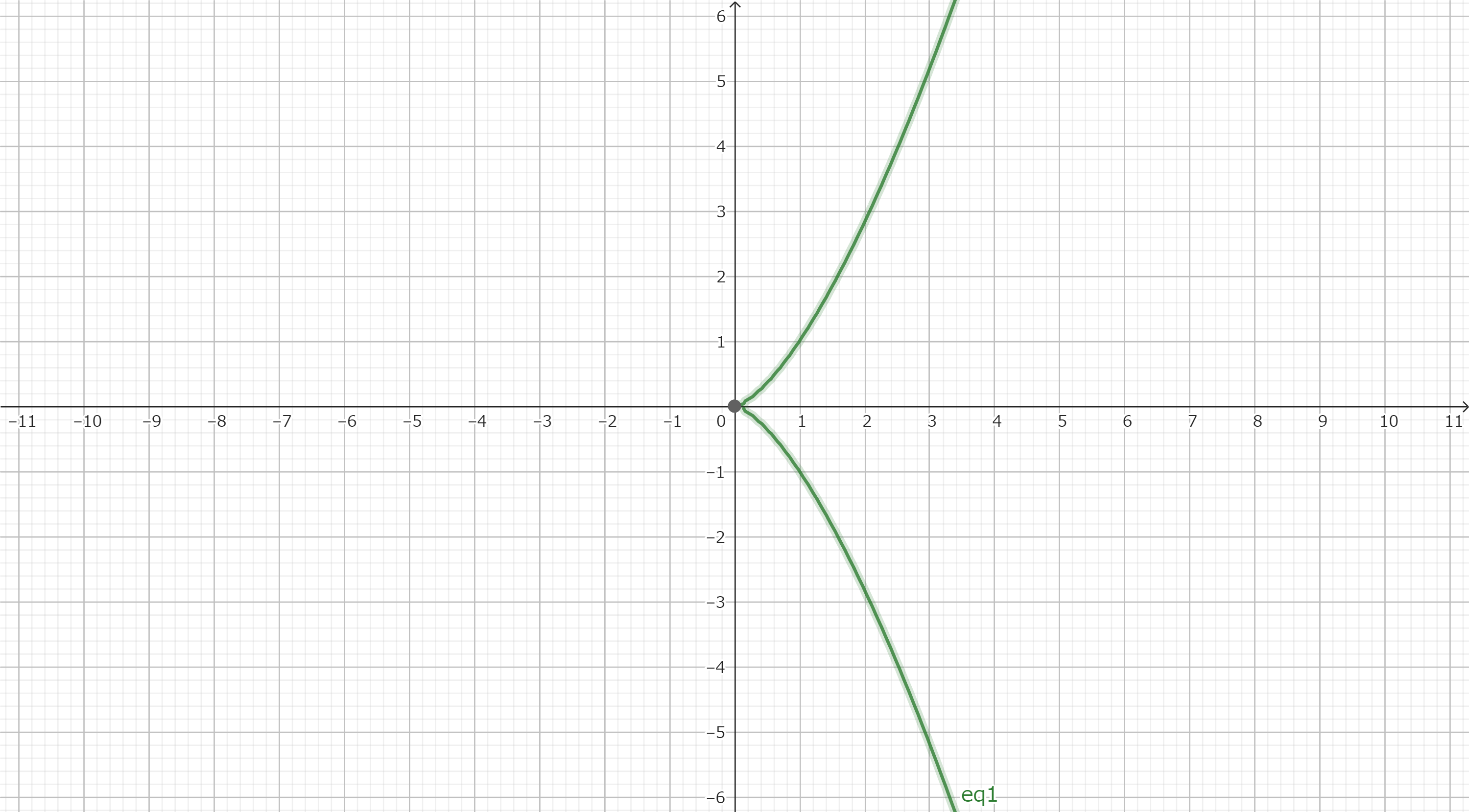
$(1,1)はy=x\sqrt{x}のほうに含まれるので$
$(x\sqrt{x})'=\frac{3}{2}\sqrt{x}$より、接線の方程式は$y=\frac{3}{2}x-\frac{1}{2}$となる。
$接線とy=-x\sqrt{x}の交点の座標は-x\sqrt{x}=\frac{3}{2}x-\frac{1}{2}を解くことにより、$
$x=\frac{1}{4},y=-\frac{1}{8}と求まる。$
$接線とx軸との交点が(\frac{1}{3},0)であることから、$
求める面積は
$$\int_{0}^{1}x\sqrt{x}dx+\int_{0}^{\frac{1}{4}}-(-x\sqrt{x})dx+\frac{1}{2}・\frac{1}{8}・(\frac{1}{3}-\frac{1}{4})-\frac{1}{2}・(1-\frac{1}{3})$$
$$=\frac{2}{5}+\frac{1}{80}+\frac{1}{192}-\frac{1}{3}$$
$$=\frac{27}{320}$$