15パズルのパリティと転倒数

はじめに

　$100$円ショップのセリアにはいろいろなパズルが $100$ 円(税込 $110$ 円)で売っていて、お気に入りの場所の1つです。
　ところがあるとき、こんな事件が起きてしまいました。
　私がいわゆる「スライドパズル」とか「$15$パズル」とかいわれているアレを買って、バラバラにしてそこらへんに置いておいたところ、小五次男氏が興味を示して解き始めたのですが・・・

セリアのパズル

　しばらくして、「どうしても最後が合わせられないから後やって」と言って持ってきたとき、パズルはこんな状態になっていました。

惜しいけど解けてない

　最後の「$14$」と「$15$」のコマが入れ替わってしまっています。
　実は、この配置から「$14$」と「$15$」を入れ替えてパズルを完成させることは不可能であることが知られているのですが、そのことに関して面白いエピソードがあるので簡単にご紹介します。

$15$パズルとサム・ロイド氏の懸賞金問題

　$1878$年に、パズル作家のサム・ロイド氏が「$15$パズルで、$14$と$15$ を入れ替えた状態を元に戻す」という問題に、当時としては破格の大金である $1000$ ドルの賞金をかけて出題しました。

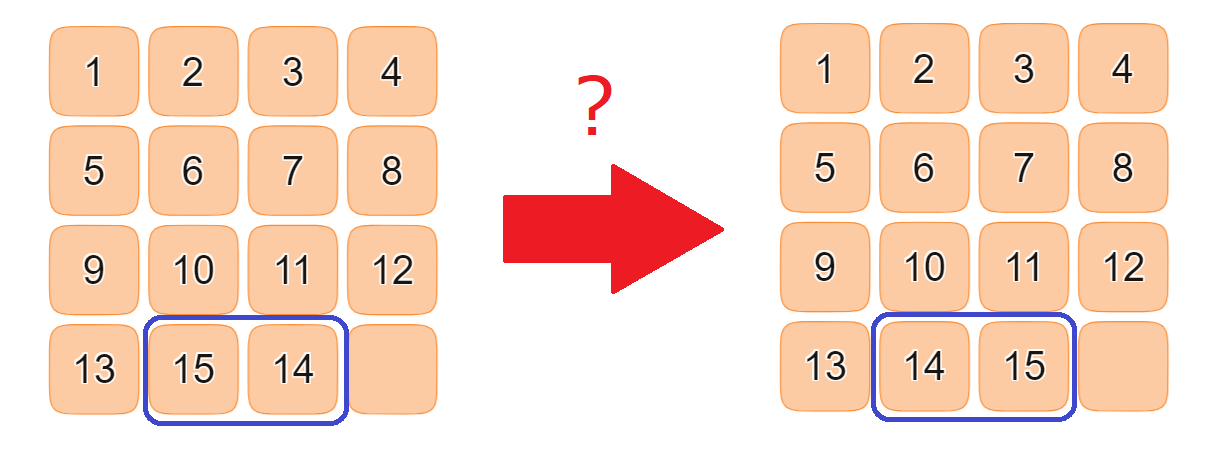　 懸賞金問題

　このサム・ロイド氏はなかなか愉快な人物だったようで、この問題が絶対に解けないことを知っていてこのような懸賞を出したのではないかとも言われています。
　もちろん、懸賞金を受け取る人は現れませんでした。

　では、この問題が解けないことを証明しましょう。

転倒数とパリティ(偶奇)

　まず、議論をシンプルにするために、$15$ パズルの配置を次のように一列に並べて数列として表示することにしましょう。

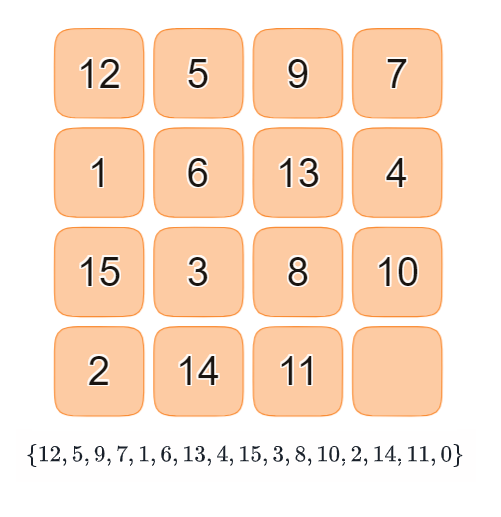数列に置き換える

　一目瞭然とは思いますが、左から右、上から下の順番に数字を並べて数列を作っています。空白の部分にはゼロを入れています。

$\{12,5,9,7,1,6,13,4,15,3,8,10,2,14,11,0\}$

　次に、「転倒数」というものを考えます。
　次のように計算します。

　例えば、第$8$項は $4$ ですが、第$8$項の前にある項のうち $4$ より大きいのは $12,5,9,7,6,13$ の $6$ 個あります。各項で同様に数えて、その総和が転倒数となります。

　具体的に計算しましょう。$\{12,5,9,7,1,6,13,4,15,3,8,10,2,14,11,0\}$ の転倒数は

$0+1+1+2+4+3+0+6+0+8+4+3+11+1+4+15=63$

　で、$63$ となります。

　ここで、$1$ つだけコマをスライドすると、転倒数がどのように変化するか考えてみましょう。
　例えば $11$ のコマを右にスライドすると $\{12,5,9,7,1,6,13,4,15,3,8,10,2,14,0,11\}$ の配置となり、転倒数は

$0+1+1+2+4+3+0+6+0+8+4+3+11+1+14+4=62$

となります。

　あるいは、$10$ のコマを下にスライドすると $\{12,5,9,7,1,6,13,4,15,3,8,0,2,14,11,10\}$ の配置となり、転倒数は

$0+1+1+2+4+3+0+6+0+8+4+11+10+1+4+5=60$

となります。

　コマを $1$ つスライドすると転倒数の偶数・奇数が交代したことに注目してください。
　実は、配置にかかわらず、コマを $1$ つ動かすごとにパリティ(偶奇)は必ず交代するのです。

　次に、パズルの盤面をチェス盤の模様に塗り分けてみます。すると、コマを一つ動かすごとに、空きマスの位置の黒白が入れ替わります。

チェス盤のように塗り分ける

　偶数回動かすと空きマスは黒い位置に、奇数回動かすと白い位置に移ります。したがって、空きマスの位置の黒白と転倒数のパリティが連動することになります。

サム・ロイド氏の懸賞金問題の答え

　サム・ロイド氏の懸賞金問題は不可能であることがこれでわかりました。
　 (再掲)懸賞金問題

　左の配置の転倒数は $16$ で偶数、右の配置の転倒数は $15$ で奇数ですが、空きマスの位置は同じです。これでは、どんな操作をしても左の配置から右の配置にすることはできません。

セリアのパズルのパリティ

　さて、小五次男氏が解こうとしていた問題についてあらためて見てみましょう。

このような操作は可能か

　左の配置の転倒数は
$0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+0=0$
で偶数。
　右の配置の転倒数は
$0+0+0+0+0+0+0+0+0+0+0+0+0+0+0+15=15$
　で奇数。
　左の配置と右の配置ではパリティが異なります。
　そして、空きマスの位置の色は同じです。
　したがって、このような操作は不可能なのです!
　
　小五次男氏は、サム・ロイド氏がしかけた罠と同様の罠にはまってしまっていたのでした……。

Desmos ゲーム

(2023.7.23追記)
ここまで読んで、「実際に遊んで確かめてみたい!」と思った方のために、Desmosでスライドパズルを作ってみました。

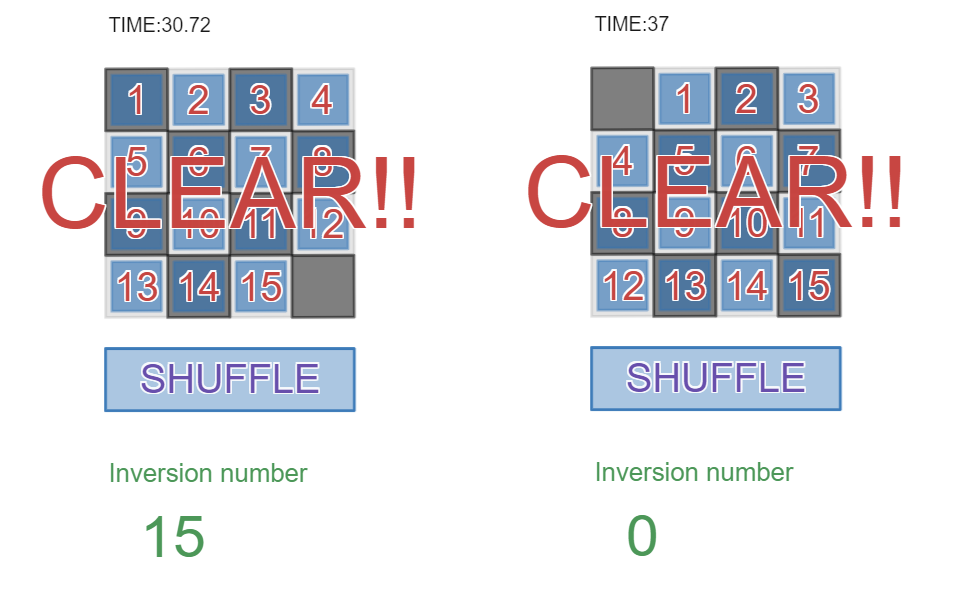クリアパターンが２種類のスライドパズルゲーム

Desmos:スライドパズルと転倒数(inversion number)

通常のスライドパズルと違い、クリアパターンが２種類あり、どちらか片方のパターンにしかなりません。

しかし、この記事を読んだ方であれば、空きマスの位置の黒白と転倒数(inversion number)のパリティで、どちらのクリアパターンで解けばいいのか即座に判断できることでしょう。

是非、実際に遊んで確かめてみてください!

おわりに

　ここで勘違いしないで欲しいのですが、セリアのパズルは決して不良品でも劣化コピーでもないということです。商品パッケージの左上にある説明を読んでみると・・・

(再掲)セリアのパズル

説明文

　ちゃんと、左上が空きマスになるように戻せ、と書いてあります。
　一般的な $15$ パズルは右下が空きマスになるようにしているのに、なぜ左上を空きマスにしたのでしょうか。

　これは私の完全なる妄想なのですが、おそらくこれを作った人は、意図的に一般的な配置とは異なる配置にしたのではないでしょうか。
　そして、サム・ロイド氏の懸賞金問題に悩む人たちのように、不可能な配置に挑戦しようとする人たちを想像してニヤニヤしていたのではないでしょうか。

　……考えすぎですかね?
　どちらにしても、この配置が意図的なものであることは間違いないと思います。というわけでセリアのパズルはあなどれないというお話でした。
　
　ほかにもいろいろ面白いパズルが置いていたりしますので、みなさんも$100$円ショップでパズル探しをしてみてはいかが?