とある無限積を一般化してみた
注意
本ページは完全な回答を与えるものではなく、あくまでも筆者の思い付きで書いているものとなります。
厳密な話しか受け付けない人はブラウザバック推奨です。
お久しぶりです！
今回は、次のような無限積の形式的べき級数展開についての問題を考えてみました。
では、さっそく問題を見ていきましょう。
$z_1,z_2,...,z_n,$$\lambda_1,\lambda_2,...,\lambda_n,$$T_1,T_2,...,T_n$なる複素数列に対して以下の様な無限積を考える。
\begin{eqnarray}
f(z_1,z_2,...,z_n)= \prod_{k=1}^{\infty}(\lambda_1T_1^{k-1}z_1+\lambda_2T_2^{k-1}z_2+\cdots \lambda_nT_n^{k-1}z_n) \\
\end{eqnarray}
この無限積の形式的べき級数展開を求めよ。すなわち、以下の形で表せ。
\begin{equation}
\sum_{k_1,k_2,...,k_n=0}^{\infty}A_{k_1,k_2,...,k_n}z_1^{k_1}z_2^{k_2}\cdots z_n^{k_n}
\end{equation}
【解】
\begin{eqnarray}
f(z_1,z_2,...,z_n)&=&(\lambda_1z_1+\lambda_2z_2+\cdots +\lambda_nz_n)\\&&
(\lambda_1T_1z_1+\lambda_2T_2z_2+\cdots +\lambda_nT_nz_n) \\&&
\cdots \\&&
(\lambda_1T_1^{k-1}z_1+\lambda_2T_2^{k-1}z_2+\cdots \lambda_nT_n^{k-1}z_n)\\&&
=(\lambda_1z_1+\lambda_2z_2+\cdots +\lambda_nz_n)f(T_1z_1,T_2z_2,...,T_nz_n)
\end{eqnarray}
より、$z_1^{k_1}z_2^{k_2}\cdots z_{n}^{k_n}$の係数を比較することで次の漸化式を得る。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(1-\mu)A_{00\cdots 0}=0\\
(1-\mu T_{l_1}^{k_{l_1}}T_{l_2}^{k_{l_2}}\cdots T_{l_r}^{k_{l_r}})A_{\cdots 0k_{l_1}0\cdots 0k_{l_2}0\cdots 0k_{l_r}0\cdots}=
\sum_{m=1}^{r}\lambda_{l_m}\cdots T_{l_{m-1}}^{k_{l_{m-1}}}T_{l_m}^{k_{l_m}-1}T_{l_{m+1}}^{k_{l_{m+1}}}\cdots A_{\cdots k_{l_{m-1}}k_{l_{m}}-1k_{l_{m+1}}\cdots}\\
(1-\mu T_1^{k_1}T_2^{k_2}\cdots T_{n}^{k_n})A_{k_1k_2\cdots k_n}
=\sum_{l=1}^{n}\lambda_{l}\cdots T_{l-1}^{k_{l-1}}T_l^{k_l-1}T_{l+1}^{k_{l+1}}\cdots A_{\cdots l-1ll+1 \cdots}
\end{array}
\right.
\end{eqnarray}$
この漸化式を解くことで終了！
n=1の場合
\begin{eqnarray}
\left\{
\begin{array}{l}
f(0)=1\\
(1-\mu)A_0=0\\
(1-\mu T^k)A_k=\lambda T^{k-1}A_{k-1}
\end{array}
\right.
\end{eqnarray}
ゆえに、求める形式的べき級数は次式となる事が分かる。
\begin{equation}
\prod_{k=1}^{\infty}(\lambda T^{k-1}z + 1)=
1+\sum_{k=1}^{\infty}\frac{\lambda ^{k}T^{\frac{1}{2}(k(k-1))}}{\prod_{l=1}^k (1-T^{l})}z^{k}
\end{equation}
n=2の場合
\begin{eqnarray}
\left\{
\begin{array}{l}
f(0,0)=1\\
(1-\mu)A_{00}=0\\
(1-\mu T_1^k)A_{k0}=\lambda_1 T_1^{k-1}A_{k-10}\\
(1-\mu T_2^k)A_{0k}=\lambda_2 T_2^{k-1}A_{0k-1}\\
(1-\mu T_1^{k_1}T_2^{k_2})A_{k_1k_2}=\lambda_1 T_1^{k_1-1}T_2^{k_2}A_{k_1-1k_2}+\lambda_2 T_1^{k_1}T_2^{k_2-1}A_{k_1k_2-1}
\end{array}
\right .
\end{eqnarray}
以上より、
\begin{eqnarray}
\left\{
\begin{array}{l}
\mu=0\\
A_{00}=1\\
A_{k0}=\frac{\lambda_1^{k}T_1^{\frac{1}{2}k(k-1)}}{\prod_{l=1}^{\infty}(1-T_1^l)}\\
A_{0k}=\frac{\lambda_2^{k}T_1^{\frac{1}{2}k(k-1)}}{\prod_{l=1}^{\infty}(1-T_2^l)}\\
\end{array}
\right .
\end{eqnarray}
また、最後の漸化式については両辺に
\begin{equation}
\frac{1}{1-T_1^{k_1}T_2^{k_2}}\prod_{l_1=1}^{k_1}\prod_{l_2=1}^{k_2}(1-\mu T_1^{l_1})(1-\mu T_2^{l_2})
\end{equation}
をかけることで次式を得る。
\begin{eqnarray}
\prod_{l_1=1}^{k_1}\prod_{l_2=1}^{k_2}(1-T_1^{l_1})(1- T_2^{l_2})A_{k_1k_2}
=
\lambda_1^{k_1}\lambda_2^{k_2} \sum_{path\in (k_1,k_2)から(0,0)へいたる道}\prod_{(l_1,l_2)\in path-(k_1,k_2)}T_1^{l_1}T_2^{l_2}\prod_{(l_1,l_2)\in (\{1,2,...,k_1\}\times \{1,2,...,k_2\}-path)}(1-T_1^{l_1}T_2^{l_2})
\end{eqnarray}
*図も参照せよ。
よって、最終的に形式べき級数は次のようになる。
\begin{equation}
\prod_{k=0}^{\infty}(\lambda_1 z_1+\lambda_2 z_2 + 1)
=1+\sum_{k=1}^{\infty}\{\frac{\lambda_1^{k}T_1^{\frac{1}{2}k(k-1)}}{\prod_{l=1}^{\infty}(1-T_1^l)}z_1^{k}+\frac{\lambda_2^{k}T_1^{\frac{1}{2}k(k-1)}}{\prod_{l=1}^{\infty}(1-T_2^l)}z_2^k\}
+\sum_{k_1,k_2=1}^{\infty}\{\lambda_1^{k_1}\lambda_2^{k_2} \sum_{path\in (k_1,k_2)から(0,0)へいたる道}\prod_{(l_1,l_2)\in path-(k_1,k_2)}T_1^{l_1}T_2^{l_2}\prod_{(l_1,l_2)\in (\{1,2,...,k_1\}\times \{1,2,...,k_2\}-path)}(1-T_1^{l_1}T_2^{l_2})\}z_1^{k_1}z_2^{k_2}
\end{equation}
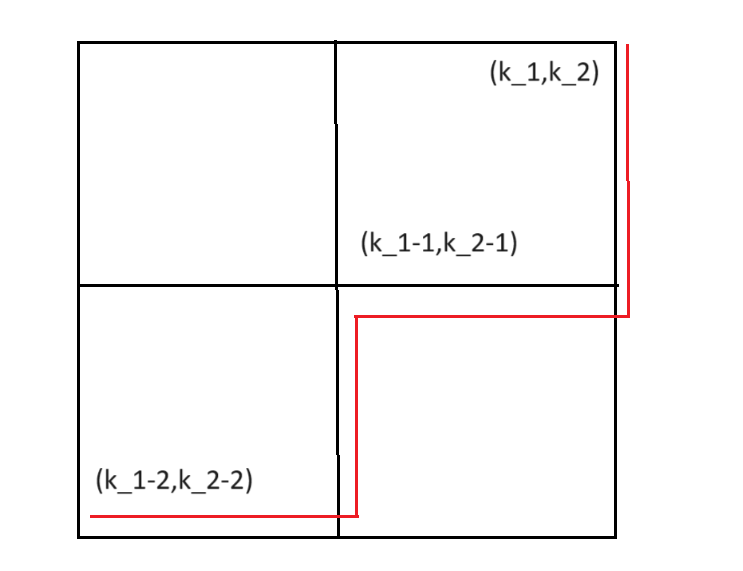形式べきの係数計算
nが3以上の自然数の場合も同様にして一般化できると思います。
でも疲れたので続きは各自でチャレンジしてみてください
今回は以上です。
よろしくね！