文献あり

ピックの定理(その１)

ピックの定理の紹介

多角形と書いたら, その境界（周）及び内部からなる図形とします。

格子多角形・格子$n$角形

平面$\mathbb{R}^{2}$上の多角形の中で, すべての頂点が格子点である多角形を格子多角形と言います。といっても後で色々な図形を呼びやすいように$n$角形なら, 格子$n$角形と呼ぶことする。

$\mathbb{R}^{2}$がわからない人は$xy$平面だと思ってください。そして格子点とはその平面上の点のなかで$x$座標と$y$座標がともに整数である点です。たとえば, $(2, 3)$とか$(67, 100)$とか。$\left(\dfrac{1}{2}, 3\right)$は$\dfrac{1}{2}$が整数ではないので格子点ではありません。

格子多角形には, 面白い定理があります。

ピックの定理

$P$を格子多角形, $I(P)$を格子多角形$P$の内部の格子点全体, $B(P)$を格子多角形$P$の境界（周）上の格子点全体とする。多角形$X$に対し, その面積を$\mathrm{Area}(X)$と書き, 集合$A$の要素の個数を$|A|$と書けば
\begin{align*} \mathrm{Area}(P)=|I(P)|+\dfrac{1}{2}|B(P)|-1 \end{align*}
が成り立つ。

以下の図の格子多角形$P$では成り立つのか確認してみます。

格子多角形!FORMULA[23][37112][0]の1つ格子多角形$P$の1つ

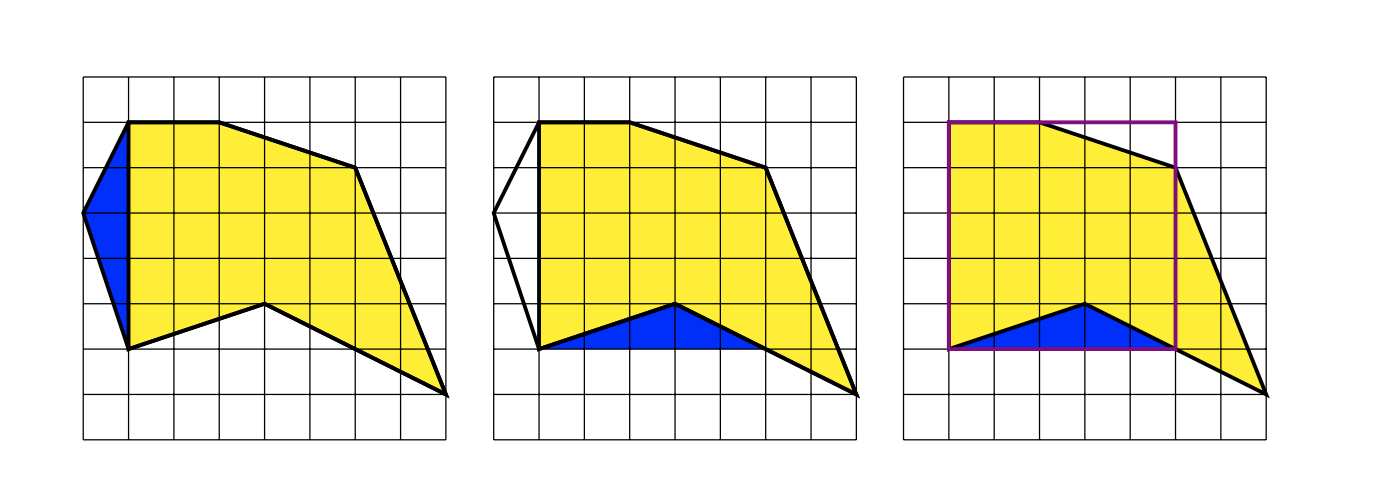
まず右のように$P$を赤い三角形と黄色の六角形に分割しましょう。そして真ん中の図のように変形し, 右側のように一部を境界が紫の正方形で囲みます。
上手に計算しよう
\begin{equation*} \left\{ \, \begin{aligned} & \mathrm{Area}(紫色で境界を囲んだ正方形)=25\\ & \mathrm{Area}(紫色で境界を囲んだ正方形の中で色が塗られてない三角形)=\dfrac{3}{2}\\ & \mathrm{Area}(黄色の図形のうち紫色で境界を囲んだ正方形からはみ出ている三角形)=4 \end{aligned} \right. \end{equation*}
\begin{align*} \mathrm{Area}(P)=25-\dfrac{3}{2}+4=\dfrac{55}{2}. \end{align*}

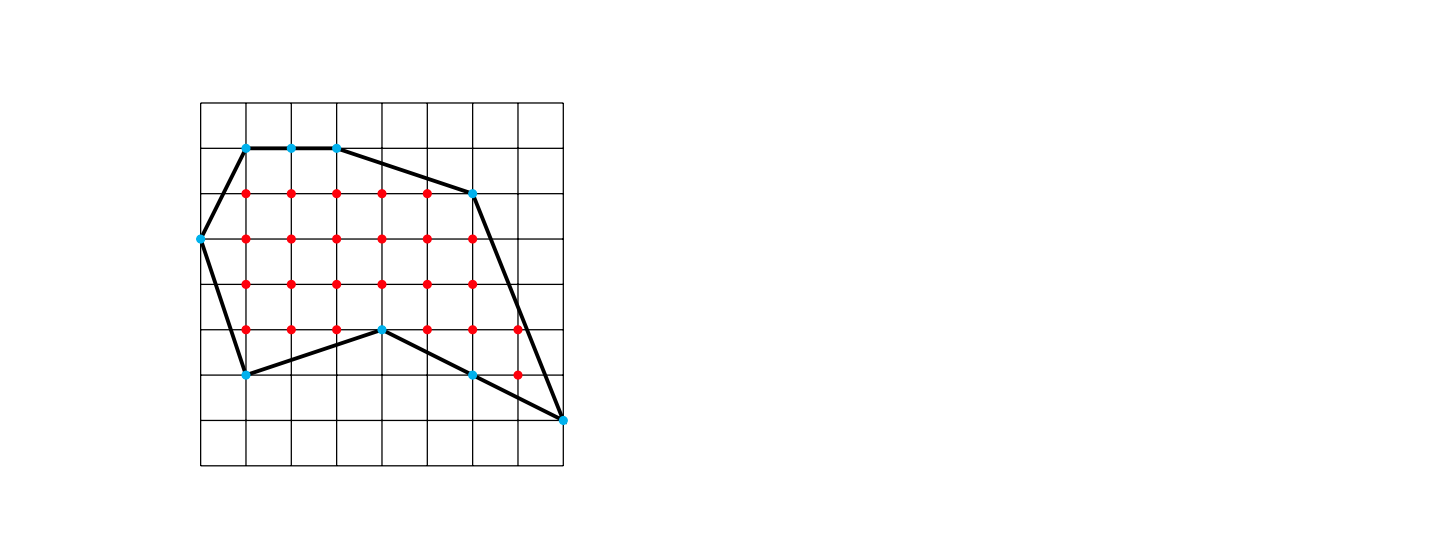
格子点を数え上げよう

そして, $|I(P)|=24, |B(P)|=9$なので
\begin{align*} |I(P)|+\dfrac{1}{2}|B(P)|-1=\dfrac{55}{2}. \end{align*}
この場合はピックの定理が成り立ちます。

ピックの定理の証明

発想は簡単。格子多角形を三角形分割し, その三角形を調べていきます。ここで格子多角形の頂点はすべて格子点なので, 三角形分割で現れる三角形は格子三角形です。

$P$を格子多角形とする。そして$S(P)$を$P$の格子点全体, つまり$S(P)=I(P)\cup{B(P)}$とします。各$q\in{S(P)}$に対し, $w(P;\, q)$を
\begin{equation*} w(P;\, q)=\left\{ \, \begin{aligned} &1\quad (q\in{I(P)}の内部) \\ &\dfrac{頂点qの内角の大きさ}{2\pi}\quad (q\in{B(P)}がPの頂点) \\ &\dfrac{1}{2}\quad （その他） \end{aligned} \right. \end{equation*}
その他というのは, $P$の境界上の点で頂点でない点ですね。そして, $W(P)$を
\begin{align*} W(P)=\sum_{q\in{S(P)}}w(P;\, q) \end{align*}
で定めます。

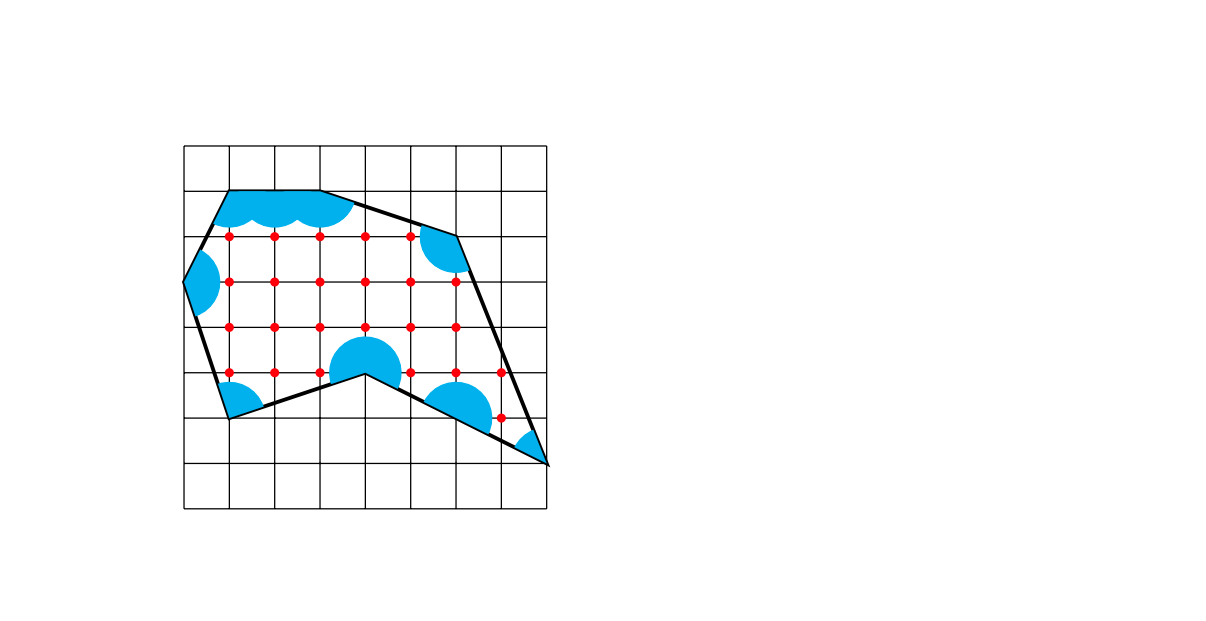
図を見てもらうとすぐにわかる。

定義2の例

最初に例として挙げた$P$を見てみましょう。そして, $q\in{I(P)}$の中で頂点であるものの全体を$C(P)$とします。すなわち$C(P)$は$P$の頂点全体の集合。これに対し, $q\in{I(P)}$だが, $q\notin{C(P)}$であるもの全体を$D(P)$とする。
\begin{align*} \sum_{q\in{I(P)}}w(P;\, q)&=1\cdot|I(P)|\\ &=|I(P)|\\ &=24 \end{align*}
であり
\begin{align*} \sum_{q\in{B(P)}}w(P;\, q)&=\sum_{q\in{C(P)}}w(P;\, q)+\sum_{q\in{D(P)}}w(P;\, q)\\ &=\dfrac{(|C(P)|-2)\pi}{2\pi}+\dfrac{1}{2}\cdot|D(P)|\\ &=\dfrac{1}{2}(|C(P)|+|D(P)|)-1\\ &=\dfrac{1}{2}|B(P)|-1\\ &=\dfrac{9}{2}-1\\ &=\dfrac{7}{2} \end{align*}
である。

$n$角形の内角の大きさの和は$(n-2)\pi$である。

これは凹多角形の場合は中学校で示したことはありませんが認めます。この定理から
\begin{align*} \sum_{q\in{C(P)}}w(P;\, q)=\dfrac{(|C(P)|-2)\pi}{2\pi} \end{align*}
を得ます。

以上から
\begin{align*} W(P)&=24+\dfrac{7}{2}\\ &=\dfrac{55}{2} \end{align*}
である。

今, 具体例を計算してみたが実は一般論として
\begin{align*} \sum_{q\in{I(P)}}w(P;\, q)&=|I(P)|\\ \end{align*}
であること, そして
\begin{align*} \sum_{q\in{B(P)}}w(P;\, q)&=\dfrac{1}{2}|B(P)|-1 \end{align*}
を導出している。よって

格子多角形$P$に対し
\begin{align*} W(P)=|I(P)|+\dfrac{1}{2}|B(P)|-1 \end{align*}

を得ます。

$W(P)$の加法性

$P$を格子多角形とし, $P$を2つの格子多角形$P_{1}, P_{2}$に分割したとき
\begin{align*} W(P)=W(P_{1})+W(P_{2}) \end{align*}
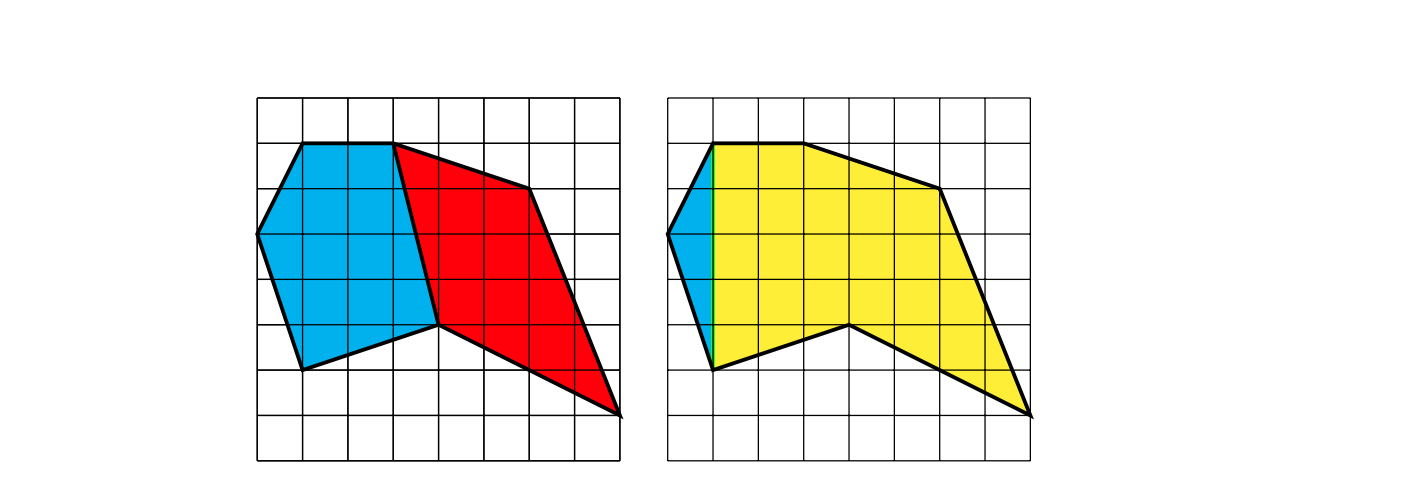多角形分割の例2つ

これは下図を見てもらえれば明らかに成り立つ定理なので省略します。といっても以下の事実には注意です。

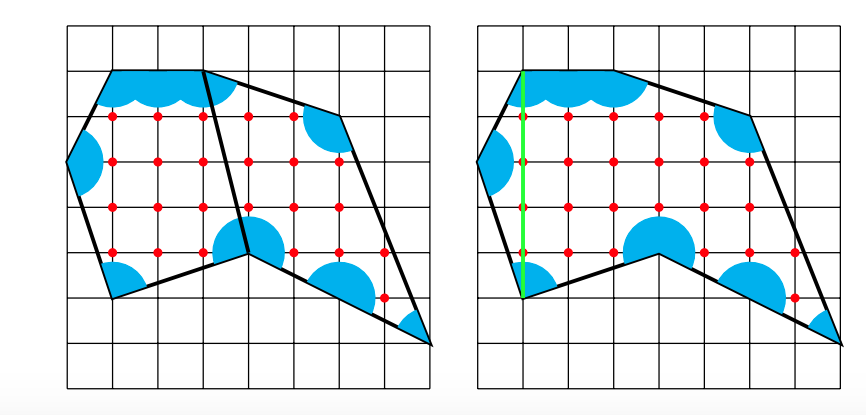命題3の例

$n$角形は$n-3$本の対角線で$n-2$個の三角形に分割可能。

$n$角形は$n-3$本の対角線で$n-2$個の三角形に分割可能です。それゆえ, それを少し弱めた主張で多角形が2つの多角形で分割できることも可能です。これも非自明ですが認めることにしましょう。

任意の格子多角形$P$に対し
\begin{align*} W(P)=\mathrm{Area}(P) \end{align*}

これは示すのが少々面倒。補題をいくつか示します。

命題3を格子長方形と格子直角三角形に限定した主張

$m, n$は正の整数とする。頂点が4つの格子点$(0, 0), (m, 0), (m, n), (0, n)$である格子長方形$R$に対し
\begin{align*} W(R)=\mathrm{Area}(R)(=(m+1)(n+1)) \end{align*}
が成り立ち, そして3つの格子点$(0, 0), (m, 0), (m, n)$である格子直角三角形$\Delta$に対し
\begin{align*} W(\Delta)=\mathrm{Area}(\Delta)(=\dfrac{1}{2}(m+1)(n+1)) \end{align*}
が成り立つ。
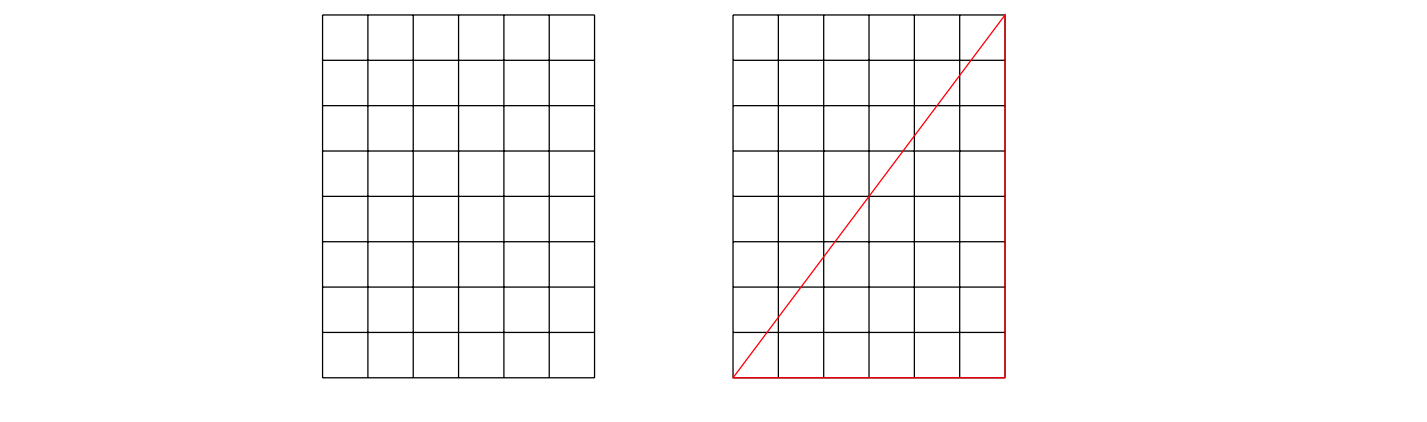格子長方形と格子三角形

一辺が$1$の格子正方形$P$に対し
\begin{align*} W(P)&=4\cdot\dfrac{1}{4}\\ &=1\\ &=\mathrm{Area}(P) \end{align*}
が成り立つのはすぐにわかる。一行目右辺は, $P$の頂点$q$に対し, $W(P;\, q)=\dfrac{1}{4}$で頂点が4つあることと$P$内部と$P$には頂点以外には境界上に格子点がないことから得られる。このことから, 頂点が4つの格子点$(0, 0), (m, 0), (m, n), (0, n)$である格子長方形$R$に対し
\begin{align*} W(R)&=W(P)\cdot{(m+1)(n+1)}\\ &=(m+1)(n+1)\\ &=\mathrm{Area}(R) \end{align*}
が成り立つことがわかる。そして3つの格子点$(0, 0), (m, 0), (m, n)$である格子直角三角形$\Delta$に対し
\begin{align*} W(\Delta)=\mathrm{Area}(\Delta)(=\dfrac{1}{2}(m+1)(n+1)) \end{align*}
が成り立つ。これは, 命題2を用いて得られる$W(R)=2\cdot{W(\Delta)}$からわかる。

命題3を格子三角形に限定した主張

任意の格子三角形$T$に対し
\begin{align*} W(T)=\mathrm{Area}(T) \end{align*}

$T$を格子三角形としその頂点を$\mathrm{A}(x_{1}, y_{1}), \mathrm{B}(x_{2}, y_{2}), \mathrm{C}(x_{3}, y_{3})$とする。ここで$y_{1}\leqq{y_{2}}\leqq{y_{3}}$としても一般性を失わない。

$y_{1}=y_{2}< y_{3}$の場合
$y_{1}< y_{2}< y_{3}$の場合
$y_{1}< y_{2}=y_{3}$の場合
$y_{1}=y_{2}=y_{3}$の場合

の4つの場合が考えられる。3.の場合で得られる$T$は合同変換を施すと, 1.の場合の$T$に帰着できる。4.はそもそも$T$は三角形を成さない。ゆえに1.と2.を調べればよい。

1.$y_{1}=y_{2}< y_{3}$の場合。1.と同様に$x_{1}, x_{2}, x_{3}$の大小関係で場合分けします。ただし, $x_{1}< x_{2}$としても一般性を失わないことを考慮してうまく場合分けします。
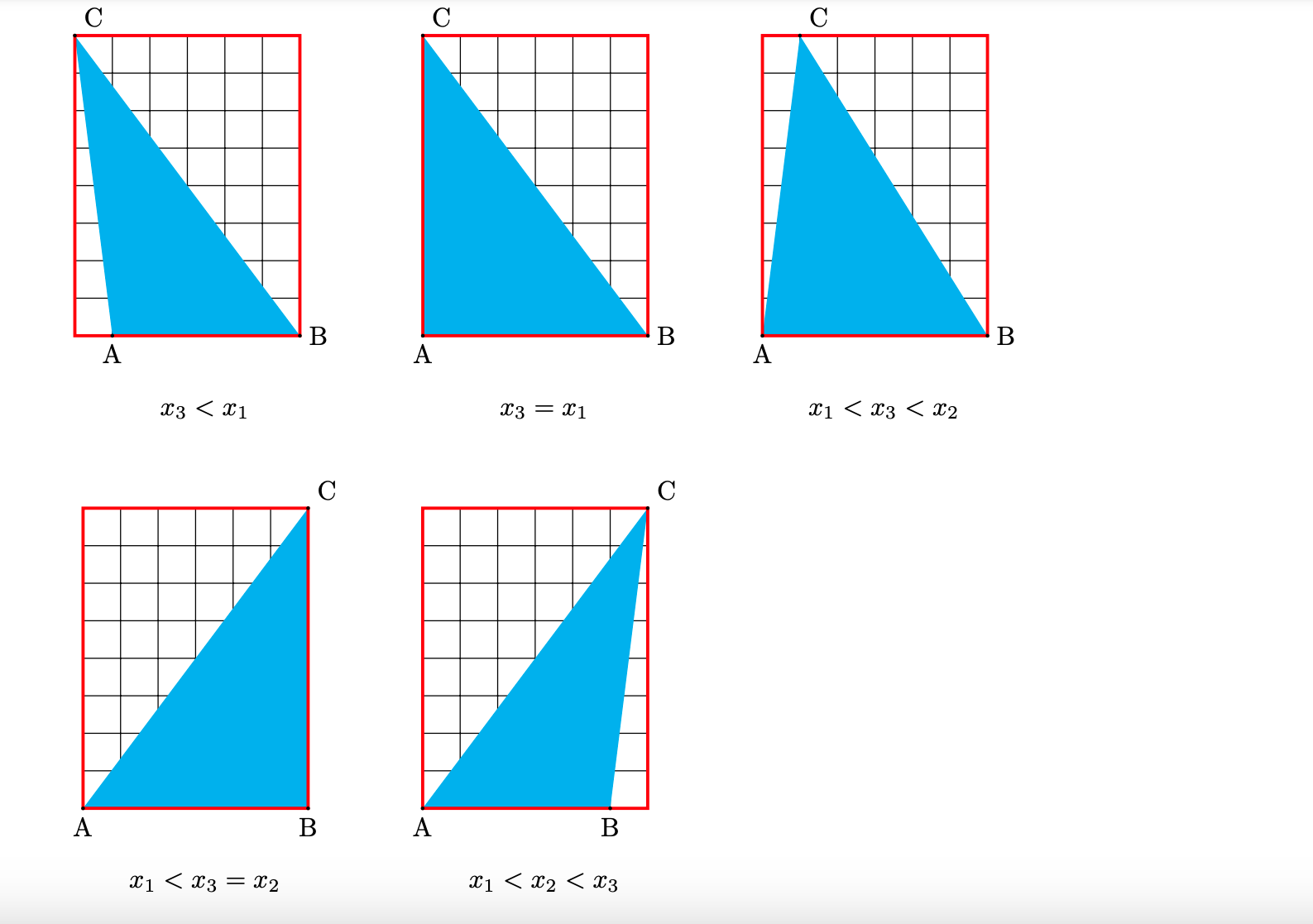1.の場合で考える必要がある図

2.$y_{1}< y_{2}< y_{3}$の場合。1.と同様に$x_{1}, x_{2}, x_{3}$の大小関係で場合分けします。ただし, $x_{1}=x_{2}$または$ x_{2}=x_{3}$または$x_{3}=x_{1}$の場合は考えなくてもよいです。なぜならこれは2つ以上の頂点が$y$軸と平行なので, 1.または4.に合同変換を用いて帰着できるからです。ゆえに$x_{1}, x_{2}, x_{3}$の3つの大小関係を考えるにしても等号が成り立つ場合は考えなくてよいです。さらに, $x_{1}< x_{2}$を調べるだけでよいです。なぜなら$x_{1}>x_{2}$の場合の$T$に合同変換を施して$x_{1}< x_{2}$の場合に帰着できるからです。

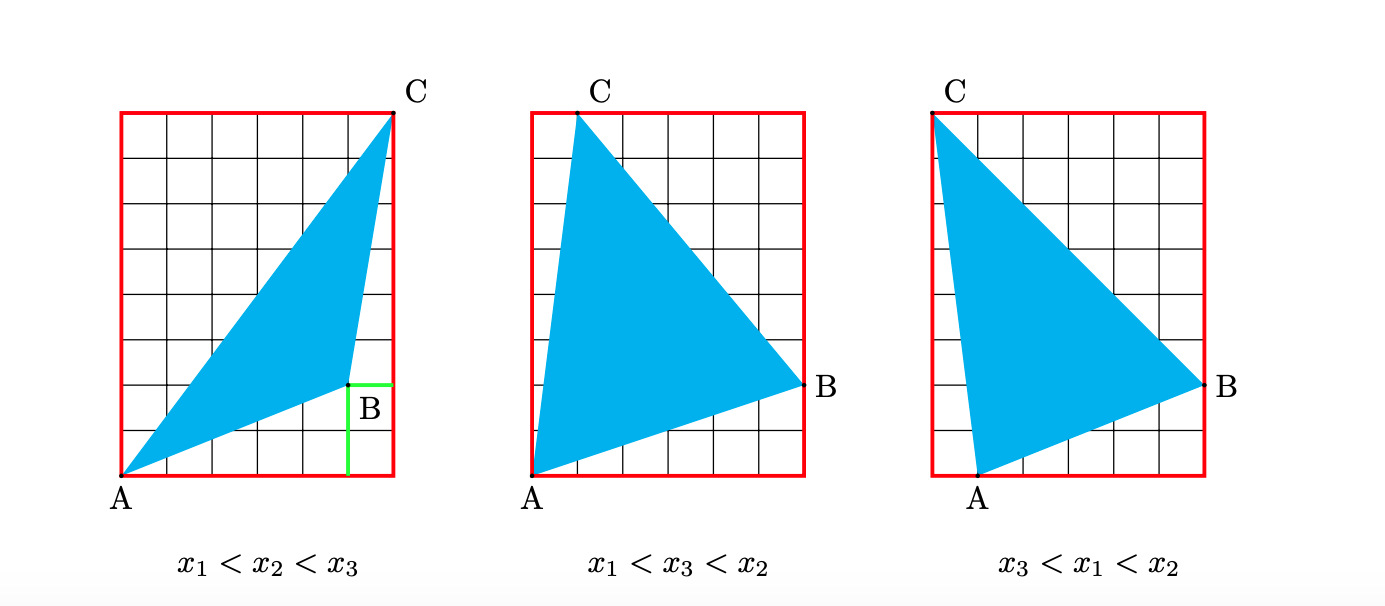2.の場合で考える必要がある図

さて上図のように格子多角形$T$は赤色の線で囲んだ格子長方形$P$で覆われていると見ましょう。その格子長方形から$T$を除いて得られる図形をいくつかの格子直角三角形や格子長方形に分解し, 命題3と補題5を用いて計算すると
\begin{align*} W(T)&=W(P)-W(P-T)\\ &=\mathrm{Area}(P)-\mathrm{Area}(P-T)\\ &=\mathrm{Area}(T) \end{align*}
を得る。

合同変換

本当は定理だけど, 合同変換とは

平行移動
回転移動
鏡映（ある直線lに対して座標平面上の任意の点$\mathrm{X}$をそれぞれその対称な点$\mathrm{X^{\ast}}$に移す変換）
の3つの変換を有限回（使わない変換があってもよい）だけうまく組み合わせて得られる変換のことである。

$P-T$の意味

$X, Y$を集合とします。このとき, $X-Y$を
\begin{align*} X-Y=\{x\mid x\in{X}かつ, x\notin{Y}\} \end{align*}
で定めます。これを差集合と言います。
高校生には形式張った表現だが$P, T$は$\mathbb{R}^{2}$の部分集合です。そして冒頭で断ったように$P, T$は辺だけではなく内部も含めるとしているので, $P-T$は格子長方形$P$から格子三角形$T$を除いた白い部分の図形を指します。

さて命題4を証明してみよう。

命題4の証明

$P$を任意の格子$n$角形とします。格子$n$角形は$n-3$本の対角線をうまく引いて$n-2$個の格子三角形で三角形分割できます。それらを$T_{i}\quad (i=1, 2, \cdots, n-2)$と置いてみると
\begin{align*} W(P)&=\sum_{i=1}^{n-2}W(T_{i})\quad (\because\, 命題3)\\ &=\sum_{i=1}^{n-2}\mathrm{Area}(T_{i})\quad (\because\, 補題6)\\ &=\mathrm{Area}(P) \end{align*}
を得る。

道具が揃ったのでピックの定理の証明をします。といっても一瞬で終わりますね。

ピックの定理の証明

$P$を格子多角形すると
\begin{align*} \mathrm{Area}(P)&=W(P)\quad (\because\, 命題4)\\ &=|I(P)|+\dfrac{1}{2}|B(P)|-1\quad(\because\, 命題2) \end{align*}