ピタゴラスの定理の証明

定番

大昔からの定番の証明
水色、桃色の直角三角形の縦$a$,横$b$,斜辺$c$で表すと面積は
$c^2=(a-b)^2+2ab$
$c^2=a^2-2ab+b^2+2ab$
$c^2=a^2+b^2$

発見

今回見つけた証明は上で示した証明に関連するものです。
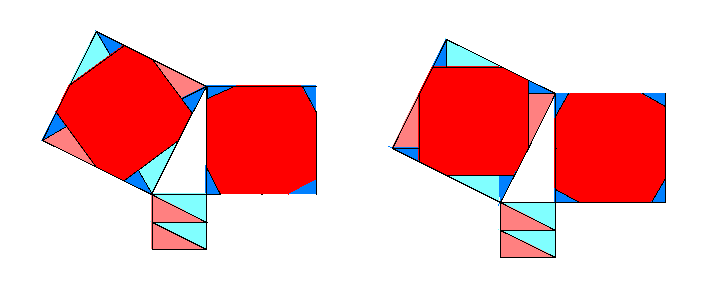見つけた証明
2パターンの証明を見つけました。

証明

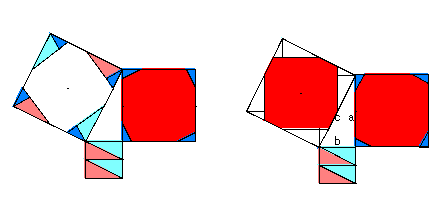
今回、青色の小さい直角三角形は縦$a'$,横$b'$,斜辺$c'$で表して、
白色の直角三角形は縦$a$,横$b$,斜辺$c$で表します。
ちなみに今回の水色、桃色の直角三角形の縦は$b$、横は$b/2$
図3左右の画像で表すと面積は
$c^2=(a^2-2a'b')+(2(b^2/2)+2a'b')$
$c^2=a^2+b^2$
証明と言いましたが、図を見ていただければ解説はいらないです。
今回みたいに Pythagorean Theorem に載ってない証明方法がまだあると思います。