微分を拡張しよう 箱と玉の微分(1) はじめに
はじめに
こんにちは。Kambing ゆっくんと申します(改名しました・・・)。数学は専門ではないので、間違いがあっても大目に見て頂けると嬉しいです。よろしくお願いします。
色の塗り分け問題を考えていたときに、箱と玉で微分を拡張できることに気づきました。どういうことかというと、箱に玉を入れることは、微分の積の法則と似ている、という気づきを得たのです。
箱と玉の微分
1階微分
1階微分はこんな感じです。
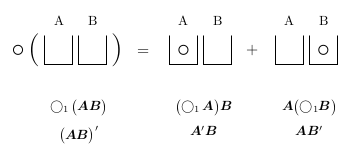 1個の玉
1個の玉
左辺は玉を箱に入れる前の状態で$(\boldsymbol{AB})'$に相当します。右辺第一項は箱Aに玉が入っている状態で$\boldsymbol{A}'\boldsymbol{B}$に相当します。右辺第二項は箱Bに玉が入っている状態で$\boldsymbol{A}\boldsymbol{B}'$に相当します。
これを$\bigcirc_1(\boldsymbol{AB})=(\bigcirc_1\boldsymbol{A})\boldsymbol{B}+\boldsymbol{A}(\bigcirc_1\boldsymbol{B})$と書きましょう。
2階微分
2階微分はこんな感じです。
 2個の玉(異なる色)
2個の玉(異なる色)
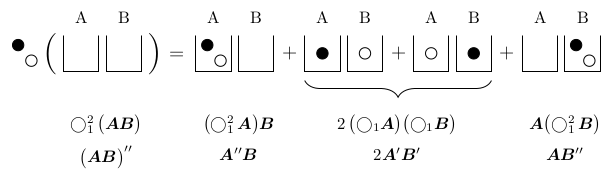
右辺第一項は箱Aに2個の玉が入っている状態で$\boldsymbol{A}''\boldsymbol{B}$に相当します。右辺第二項は箱Aと箱Bにそれぞれ1個の玉が入っている状態で$2\boldsymbol{A}'\boldsymbol{B}'$に相当します。玉の入り方は2通りあるため、係数が2となります。右辺第三項は箱Bに2個の玉が入っている状態で$\boldsymbol{AB}''$に相当します。
これを$\bigcirc_1^2(\boldsymbol{AB})=(\bigcirc_1^2\boldsymbol{A})\boldsymbol{B}+2(\bigcirc_1\boldsymbol{A})(\bigcirc_1\boldsymbol{B})+\boldsymbol{A}(\bigcirc_1^2\boldsymbol{B})$と書きましょう。より高階の場合についても、箱と玉の微分と従来の微分の間には同様の類似が成り立ちます。箱と玉という、完全に離散的な構造にも、微分と同じような演算が存在するのです!!!そして箱と玉の微分には、従来の微分にはない、色という自由度を持ちます。つまり微分の拡張とみなせます。
同じ色の2階微分
では同じ色の玉を入れるとどうなるか。
 2個の玉(同じ色)
2個の玉(同じ色)
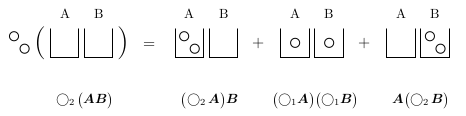
こうなりますよね。右辺第二項は箱Aと箱Bにそれぞれ1個の玉が入っている状態ですが、玉の入り方は1通りしかないので係数が1となり、通常の2階微分とは異なるものとなります。
これを$\bigcirc_2(\boldsymbol{AB})=(\bigcirc_2\boldsymbol{A})\boldsymbol{B}+(\bigcirc_1\boldsymbol{A})(\bigcirc_1\boldsymbol{B})+\boldsymbol{A}(\bigcirc_2\boldsymbol{B})$と書きましょう。箱と玉の微分の2階微分は二種類あるわけです。
ちゃんと定義しよう
ちゃんと定義しましょう。
$$ \begin{align} &\text{箱の可換則(和)}&\boldsymbol{A}+\boldsymbol{B}=\boldsymbol{B}+\boldsymbol{A}\\ &\text{箱の可換則(積)}&\boldsymbol{AB}=\boldsymbol{BA}\\ &\text{玉の可換則}&\bigcirc_n\bigcirc_m=\bigcirc_m\bigcirc_n\\ &\text{恒等変換}\;&\bigcirc_0\boldsymbol{A}=\boldsymbol{A}\\ &\text{スカラー倍}&\bigcirc_n \bigl(k\boldsymbol{A}\bigr)=k\bigl(\bigcirc_n\boldsymbol{A}\bigr)\\ &\text{和の法則}&\bigcirc_n\bigl(\boldsymbol{A}+\boldsymbol{B}\bigr)=\bigcirc_n\boldsymbol{A}+\bigcirc_n\boldsymbol{B}\\ &\text{積の法則}&\bigcirc_n\bigl( \boldsymbol{A}\boldsymbol{B} \bigr) =\sum_{k=0}^n \bigl(\bigcirc_k\boldsymbol{A}\bigr)\bigl(\bigcirc_{n-k}\boldsymbol{B}\bigr) \end{align} $$
また従来の微分で$x$に相当するものとして、もっとも基本的な箱を定義します。
$$
\bigcirc_n\boldsymbol{p}_m=\begin{cases}1 & n=m\\0 & \text{それ以外}\end{cases}
$$
この$\boldsymbol{p}_m$を大きさmの小箱と呼ぶこととします。
エクササイズ
ちょっとしたエクササイズをしてみましょう。まず$n\le m$のとき、
$$
\bigcirc_1^n\boldsymbol{p}_1^m=\frac{m!}{(m-n)!}\boldsymbol{p}_1^{m-n}
$$
となり、係数に順列が現れます。これは通常の微分の
$$
\frac{d^n}{dx^n}x^m=\frac{m!}{(m-n)!}x^{m-n}
$$
と同じで、積の法則から簡単に分かります。区別できるm個の大きさ1の小箱$\boldsymbol{p}_1$に、区別できるn個の玉を入れる場合の数が係数に現れる、と解釈できます。では同じ色の玉の場合はどうなるでしょうか。積の法則から地道に計算すると次のようになります。
$$
\bigcirc_n\boldsymbol{p}_1^m={}_mC_n\boldsymbol{p}_1^{m-n}
$$
係数に二項係数が現れます。区別できるm個の大きさ1の小箱$\boldsymbol{p}_1$に、区別できないn個の玉を入れる場合の数が係数に現れる、と解釈できます。箱と玉の微分は組合せ論と相性がよさそうです。
今後考えたいこと
物理現象を微分方程式で記述できるように、組合せ論の問題も、箱と玉の微分方程式で記述して、いろいろと考察してみる、という記事を書く予定です。ところで箱と玉の微分には、どこまで従来の微分と同じような議論が展開できるのでしょうか?実は、箱と玉の微分にもテイラー級数展開や合成関数の微分公式の類似が存在するのです。だから場合の数を求めるという問題も、級数展開して求めたりできるというわけです。かなり筆遅になると思いますが、これについても後々の記事で説明していきたいと思います。よろしくお願いします。
