【高校数学】部分分数分解の計算テクニック ヘビサイドのカバーアップ法（Heaviside cover-up method）
ヘビサイドのカバーアップ法（Heaviside cover-up method）
ヘビサイドのカバーアップ法（Heaviside cover-up method）とは，部分分数分解を実行する際の各項の係数を決定する方法です．通分して恒等式の計算をするより楽に計算できる場合が多いので紹介します．
一般的に述べるより，例を用いた方がわかりやすいので下の問題を見てください．
$\displaystyle\frac{1}{(k+1)(k-1)}$を計算しなさい．
ヘビサイドのカバーアップ法の手順
- $k+1$の根（ある多項式$P(x)$にある値$x=a$を代入した際，その多項式の値が$0$になる$x$の値$a$のことを多項式$P(x)$の根という）を求める：$k=-1$．
- $\displaystyle\frac{1}{(k+1)(k-1)}$の式から，手で$k+1$の部分を隠し（cover-upはこれに因んでいる)，隠して残った式$\displaystyle\frac{1}{k-1}$に手順1で求めた$k$の値を代入する．これで出てきた値が部分分数分解した際の$\displaystyle\frac{1}{k+1}$の係数．
- 手順1，2と同様に$\displaystyle\frac{1}{k-1}$の係数を求める．
よって，
$$\displaystyle\frac{1}{(k+1)(k-1)}=\displaystyle\frac{-\frac{1}{2}}{k+1}+\displaystyle\frac{\frac{1}{2}}{k-1}=\displaystyle\frac{1}{2}\left(\displaystyle\frac{1}{k-1}-\displaystyle\frac{1}{k+1}\right)$$
つまり，根を計算して，cover-upして，係数を求めるという3STEPを踏めばいいことになります．しかし，分母のそれぞれの多項式が二次以上になると複雑になってきます．そこで，まず，部分分数分解した後の形について述べます．
因数分解できる多項式$P(x)=(x-x_1)^{n_1}(x-x_2)^{n_2}\cdots(x-x_m)^{n_m}$について，$\displaystyle\frac{1}{P(x)}$の部分分数分解は，
$$\displaystyle\frac{1}{P(x)}=\displaystyle\sum_{i=1}^{m}\displaystyle\sum_{j=1}^{n_i}\displaystyle\frac{a_{ij}}{(x-x_i)^{j}}$$
で表される．
略（複雑なため）．詳しくは，[ 3 ]を参照してください．
$\displaystyle\frac{1}{x(x+1)^2}$の部分分数分解は，$\displaystyle\frac{A}{x}+\displaystyle\frac{B}{(x+1)}+\displaystyle\frac{C}{(x+1)^2}$の形で表せる．
ここで，各項の係数を求めるヘビサイドのカバーアップ法の主張を確認しましょう．
命題1の係数$a_{pq}$は，
$$a_{pq}=\dfrac{1}{(n_p-q)!}\displaystyle\lim_{x\to x_p}\dfrac{d^{n_p-q}}{dx^{n_p-q}}\left\{(x-x_p)^{n_p}\dfrac{1}{P(x)}\right\}$$
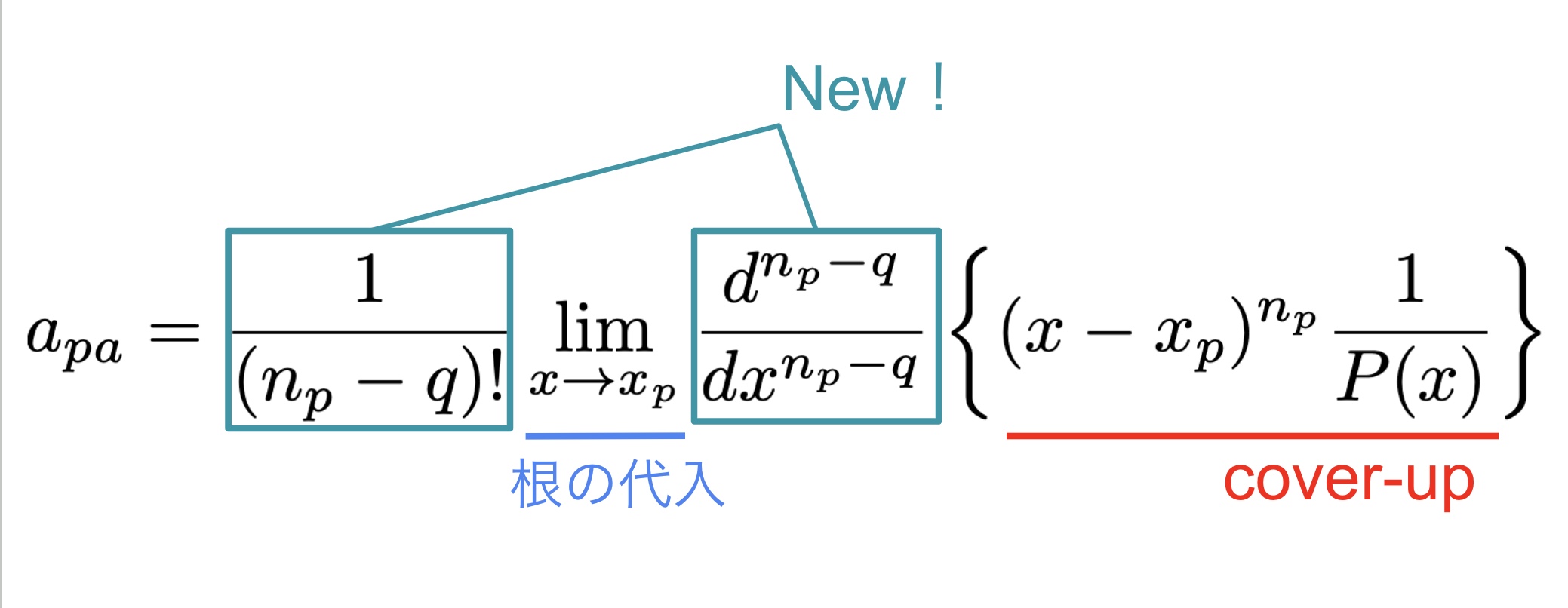ヘビサイドのカバーアップ法
※図1の$a$の添字が誤っています．正しくは$a_{pq}$．（2023年12月23日更新）
執筆中
$\displaystyle\frac{1}{x(x+1)^2}$の部分分数分解は，$\displaystyle\frac{A}{x}+\displaystyle\frac{B}{(x+1)}+\displaystyle\frac{C}{(x+1)^2}$の形で表せる．
$$A=\frac{1}{(0+1)^2},B=\frac{1}{0!}\displaystyle\lim_{x\to -1}\frac{d}{dx}\left(\frac{1}{x}\right)=\displaystyle\lim_{x\to -1}\frac{-1}{x^2}=-1,C=\frac{1}{-1}$$
よって，
$$\displaystyle\frac{1}{x(x+1)^2}=\displaystyle\frac{1}{x}-\displaystyle\frac{1}{(x+1)}-\displaystyle\frac{1}{(x+1)^2}$$
補足：$0!=1$とします．