証明幾何作問
少し前に作った問題の解答です。
分野はG、難易度はOMCで300点問題くらいだと思います。(公開した問題とは少し変えています。)
円$O$上に点$A,B,C,D$ を
$CD< CB< AB< AD=AC$
となるように配置する.
また,線分$AC$と$BD$の交点を$E$,三角形$ECD$の外接円の点$D$における接線と直線$AB$の交点を$F$,円$O$の点$D$における接線と円$O$の点$A$における接線の交点を$G$,$AG$と$FD$の交点を$H$とする.四角形$ABCD$と四角形$ADGF$が相似となることを示せ.
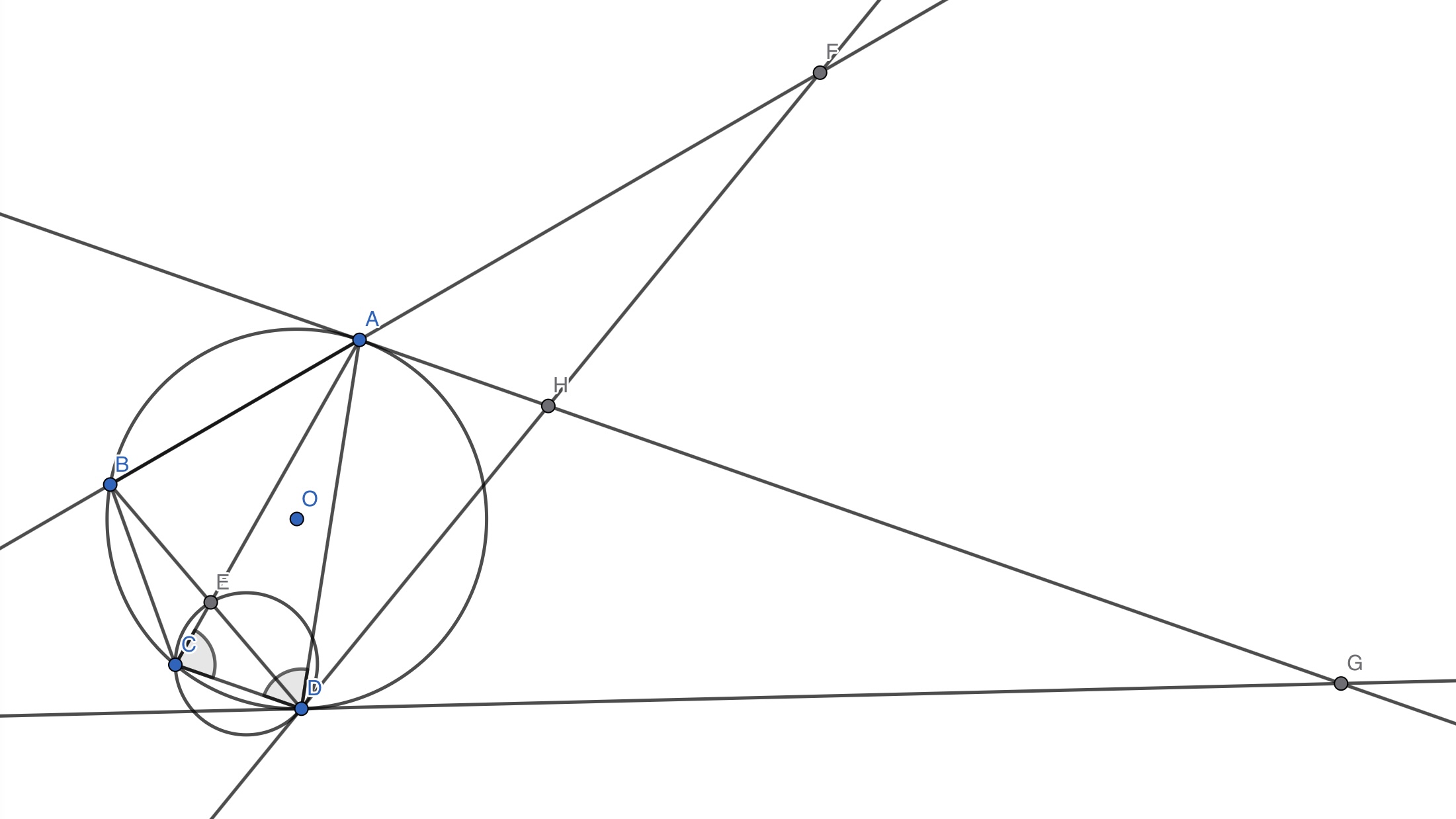
元々は求値問題だったけれど、図形が存在するように値を設定するとその値のいずれかにルートがつく感じになって計算が面倒になるという理由で、「これがわかったら解けるだろ」というのを問題にしました。
解説を読む前に少し考えておくことをおすすめします。
解説まで少し空けておきます。
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
〜解説〜
先に回転相似について説明する。(これは有名であると思うので知っている方は飛ばしてもよい。)
△ABCと△AB’C’が相似になるように点B’、C’をとると、△AB’Bと△AC’Cが相似になる。
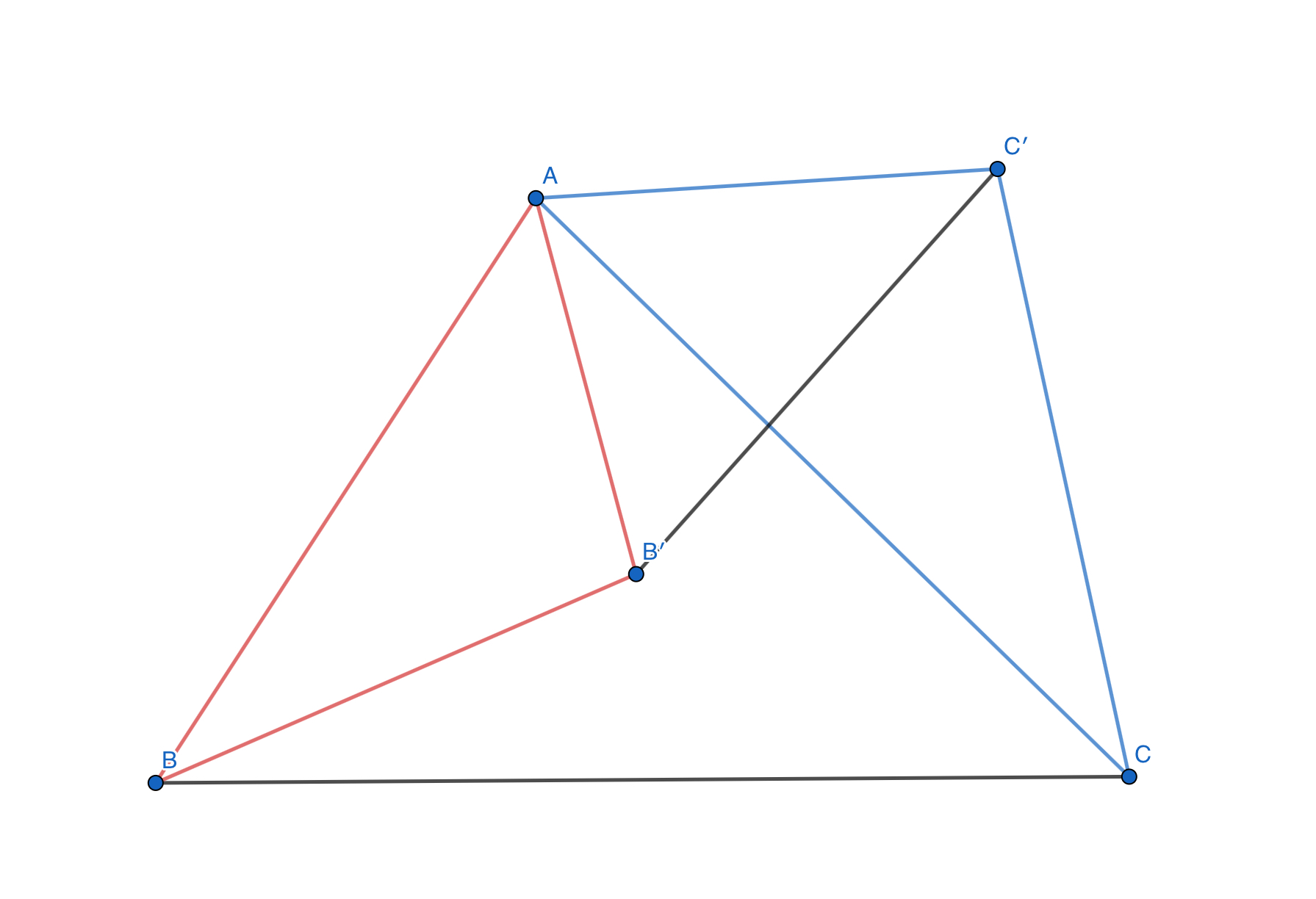 回転相似
回転相似
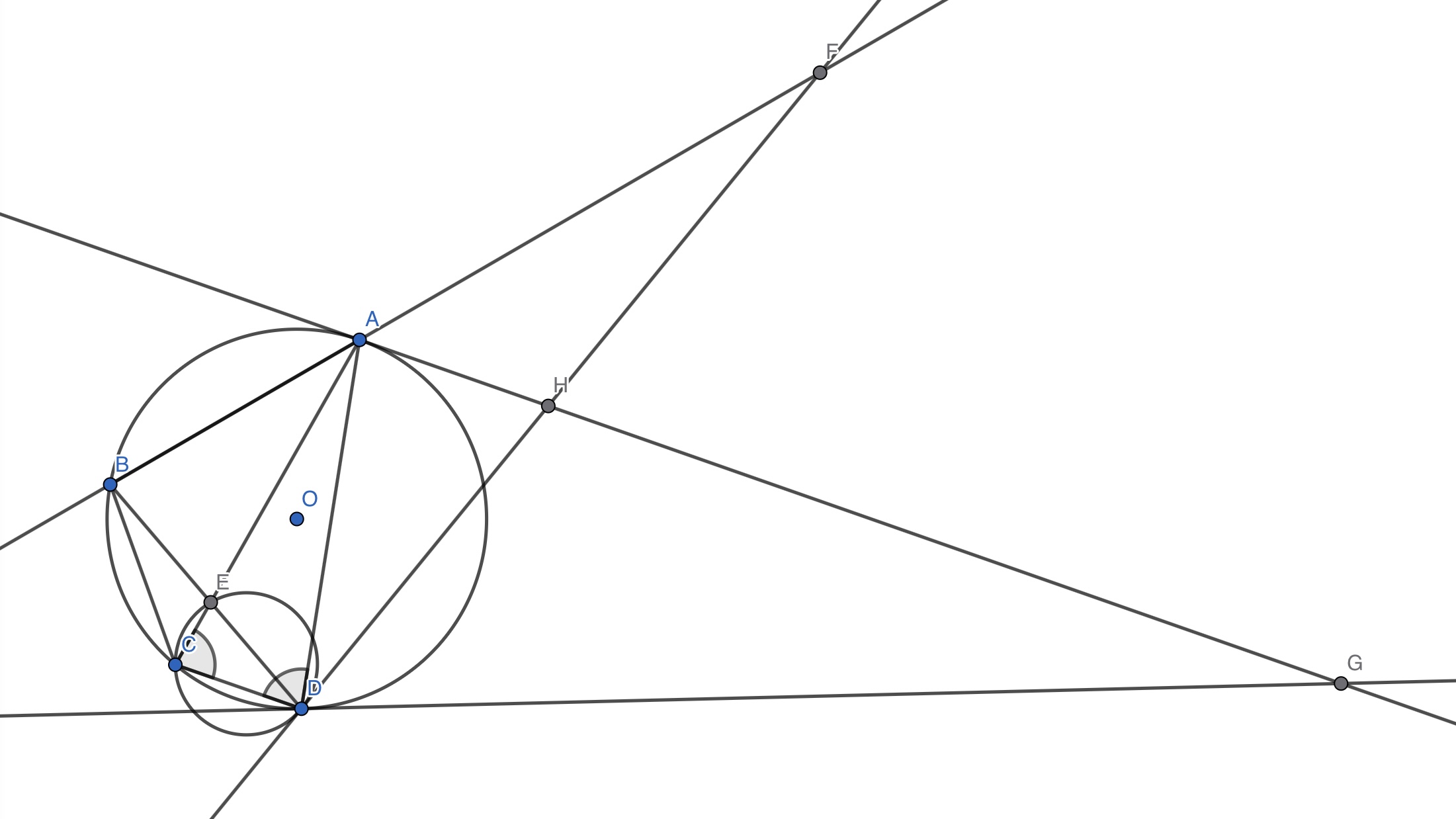 (図を見つつ解答を読む人用)
(図を見つつ解答を読む人用)
円周角の定理、△CEDについての接弦定理、△BADについての接弦定理より、
$$角ACD=角ADC=角FBD=角FDB=角GDA=角GAD$$
これより、△ACDと△FBD、△GADが相似であることがわかった。また、△ACDと△FBD、△FBDと△GADの回転相似より
△BCDと△FAD、△ABDと△FDGがそれぞれ相似であることがわかった。
………あれ、これ2組の相似な三角形の相似比が同じで、それぞれ同じ向きに組み合わさってね?
っていうのに気づいたら勝ちです。
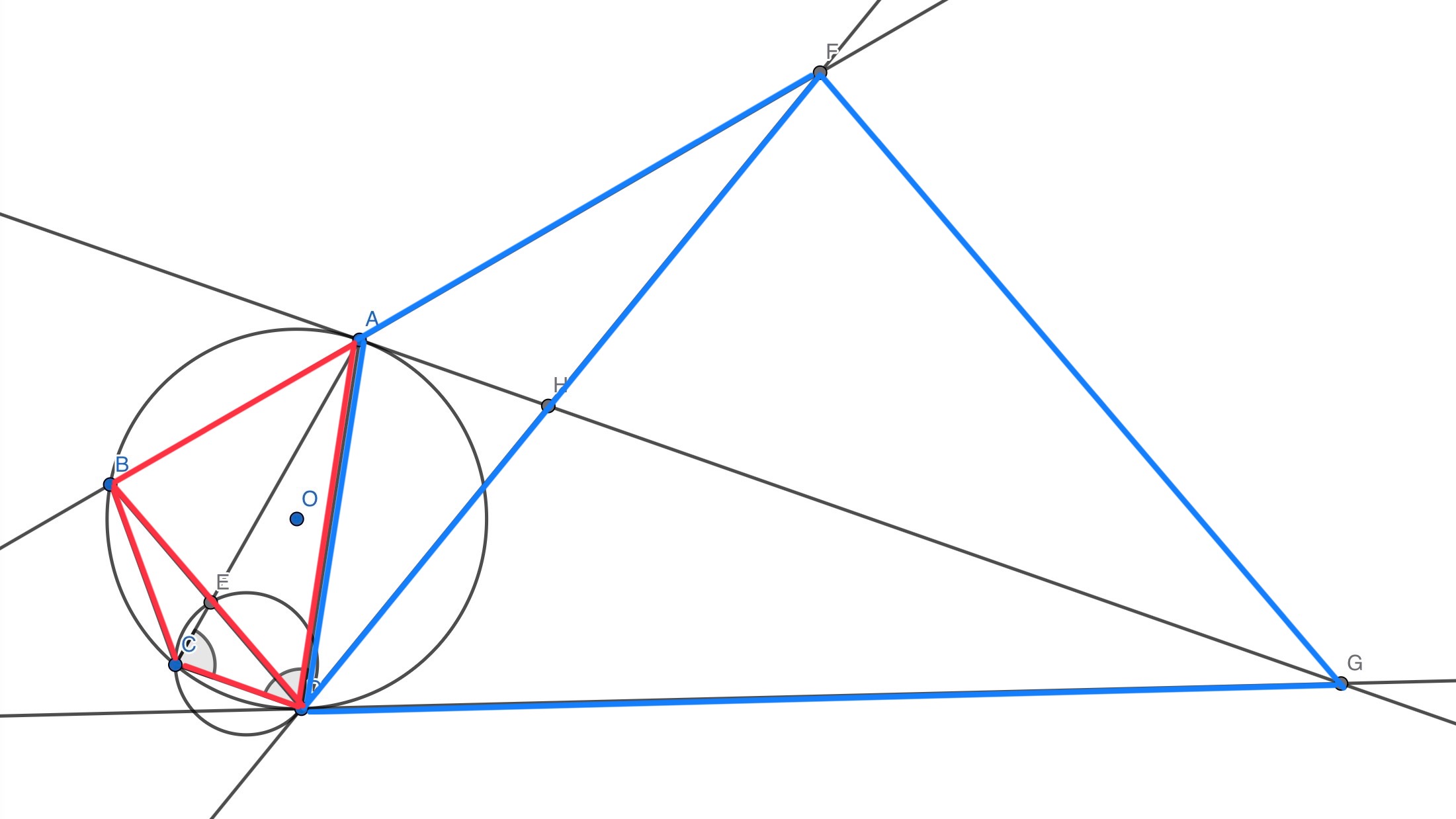 geogebraで色付けしようとしたら変になるから写真アプリでやった
geogebraで色付けしようとしたら変になるから写真アプリでやった
ということで題意は示された。めでたしめでたし……点Gは求値問題を解く上でのヒントとして設置したからヒントとして扱えなくて悔しい
辺の長さの関係が少し変わっても成り立つから条件をもう少し緩くしてもよかったかもしれませんね。
いかがでしたか?この問題は個人的に面白い問題だと思ったのでOMCで出題したかったのですが、僕の実力がなく、提出できるようになるまで時間がかかるので世に放流しました。早くwriterになりたいですね。
間違い・別解等があれば容赦なくコメント欄で指摘ください。読んでくださりありがとうございました。