第3回高校生数学コンテスト in Hamamatsu 解いてみた

　意味わからんタイミングでの公開

何があった？

　途中まで書いてたんですが放置してて、結果書くタイミングも出すタイミングも逸していました　時が流れ、なんとなく下書きを見たらあったので一部だけでもまあ出すかー、、という

$$ \text{― ネタバレ防止用空白 ―}$$

---

　難易度順になっているとは限らない，とは書いてありましたが私は一般人なのでとりあえず1番を見ました．

• うーん，何ですかこれは　複素数何も分からないんですが
• 何も分からんしとりあえず $x=a+bi$ みたいな感じでおいてやるか
• あの，なんか解けたんですが

一応解法を置いておきます

　$x=a+bi,y=c+di,z=e+fi$ として，$ace$を求めます．まず $x^2+y=a^2-b^2+c+(d+2ab)i$ が実数なので $d=-2ab$です．同様にして $f=-2cd$ および $b=-2ef$ が分かります．これらを辺々掛け合わせると $bdf=-8abcdef$ となり，$0$ でないことを思い出して約分みたいにすると $\boxed{abc=-\frac18}$ が分かりました．必要性で絞り込んだだけなので一応これを満たす $a,b,c,d,e,f$ の存在を言っておく必要はあって，まあ全部 $-\dfrac12$ にしたりしてあげれば良いです．

　ちょっと嫌な感じがして身構えちゃいましたがまあ1番～って感じで簡単でしたね．（全員が完答していた ←！？）　十分性を忘れても減点されなかったらしい，まじか

　まあ2番を見ます．

• うーん，何ですかこれは
• とりあえずこういうのは実験をすると良いことが知られているのでしてみる．
• 例えば全部平らな場合は $\displaystyle{\frac57,\frac57,\frac57,\frac57,\frac57,\frac57,\frac57}$ で，合併後の面積のminは $\dfrac{10}7$．
• 大きいところをバラしてみる．たとえば $\displaystyle{1,\frac12,\frac12,1,\frac12,\frac12,1}$ としてみると，面積のminは$\dfrac32$．小さくなっている．
• $\displaystyle{1,\frac13,1,\frac13,1,\frac13,1}$ としてみると，面積のminは$\dfrac43$．さらに小さくなった．
• どうせもっと小さくできるのでしたいが，微妙な雰囲気があるので一旦下から押させたい．
• さんざん実験したけど「左から貪欲に取っていく」のが一番お得じゃないですか？（右にたくさん残せると嬉しいので）
• 答えを $\alpha$ とでもおいてみる．左から取っていって $\alpha$ 以上になったら切るみたいにやったとき，左側の二区間は最大でもそれぞれ長さが $\alpha+1$ 未満になる（各区間の長さが $1$ 以下なので）．
• ってことは $3\alpha+2=5$ みたいになる $\alpha$ だと嬉しそうで，これは $1$ です．
• てことで $C\geq 1$ がいえた．どうせ構成があるので見つけよう．
• $\displaystyle{\frac12,\frac12,1,\frac12,\frac12,1,1}$ で行けますね，解けたー

なんで行けてるのか分からないあなたのために

　左から $3$ 番目と $6$ 番目の $1$ に注目します．鳩ノ巣原理的なノリでこの $1$ を含まない合区間が存在して，それの長さは（良い感じに区切られて）最大でも $1$ になると分かるので，良いです．（自分はこの感じのモチベで構成をしましたが，同じようなことをしている人は周りには見当たりませんでした，確かに微小なやつを取ってくるみたいなモチベの方が自然ではある...）

　ここまで $20$ 分くらい（記述は後回し）．調子いいですねー．

　4番の幾何が目にめっちゃ入って来てヤバいんですがとりあえず3番を見ます．

• ここで差が付く！みたいな見た目をしていて最悪．多項式も整数もできないので困った．
• なんか最近のOMCでこんな感じの雰囲気の合成関数みたいなやつ出てなかったか？マジで自分だけ解けない問題になりそうでまずい！
• まあ解きます．$P(2024)=P(P(P(P(1))))$ ですねー．
• 自明な下界とかあるんですか？
• $P(P(P(1)))=2024$ 構成したくないですか？します　→できません
• どうせmodでなんか不変みたいなのではなく？　→違います
• 詰まったらトイレに行け　→何も浮かびません
• どうせ二次関数で綺麗に構成！みたいなのではなく？　→よくわかりません
• 不可能！

になってしまい諦めました（頭悪そうすぎる）．素養がありません．
というか $P(x)-P(y)$ が $x-y$ の倍数になる話，人生で100回くらい見てきたはずなのに頭のどこにもなかったのダメすぎ～って感じがします．

　最終的にこの問題に戻ってくることはなかったわけですが，無理っぽい問題に0.8時間くらい無意味な粘着をしてしまったことはかなり反省．

　4番を見ます．幾何だ！解けるぞ！　←この人はJMO2024本選4を落としています

• まずは図を書きます．
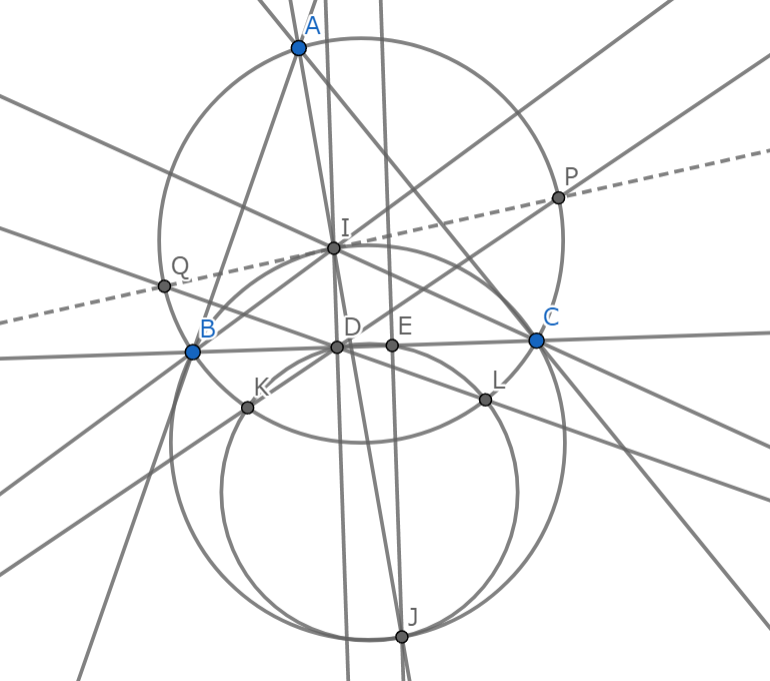  問題4-図1

• まあ直径を$DJ$とする円ってのは$A$-傍接円と辺$BC$の接点を$E$としたときの円$DEJ$と見た方が良い．

• こんなんどうせ$PQ$と円$BIC$が接するってオチだろ！w ←嘘です

• とりあえず$D$と$E$は$BC$の垂直二等分線に関し対称だから$BKLC$は等脚台形だな．

• ってことは$\angle DPQ=\angle KLD=\angle QDB$だから円$DPQ$は$BC$と接する．

• じゃあ$BC$と$PQ$の交点を$T$としたらどう考えても$TD\neq TI$だから$PQ$と$BIC$接しないじゃ～ん，何してんの

• うーん，$J$の左側に良い感じの共点あってこれ取ったらうまくいったりしませんか →$S$とする

• え，てかそしたら根心的なノリで方べきを回すと$SKIP$共円が言えて，逆側でも$SLIQ$共円が言えるので終わってませんか

　実際にはこんなにスムーズには議論が進んでいないのですが（$PQ$と$BIC$が接すると思い込んだところで同一法を回しに行ったりしてしまった），$S$を取ってみたらあっさり解けてしまいました...

　この後，答案を書いたり見直しをちょっとしたり3を眺めていたり（進捗が生えない）したら残りが40分くらいに．5に行きます．

• ARCのBとかにありそうな見た目すぎる
• 何かしらの不変量とかがあるみたいなやつですか
• 転倒数絡みとかでいろいろ考えてみるが，特にパッとしたものが浮かばない...
• とりあえず1つの$n$で行けたらそれ以上の$n$は全部行けるな？
  演習：なぜ？

  　$n+1$人をソートしたいときは，$1\sim n$をソート→$2\sim n+1$をソート→$1\sim n$をソート，とやればいいので帰納法が回ります．
  

• まあどう考えても$n=3$は不可能で，例えば$132$は$312$にしか移れないので無理．
• $n=4$もどうせ不可能で，例えばパリティ的なノリで死にそうな$1243$を考えてみると，
  $$ 1243\leftrightarrow 1423\leftrightarrow 4123\leftrightarrow 4321\leftrightarrow 2341\leftrightarrow 2314\leftrightarrow 2134\leftrightarrow 2431\leftrightarrow 4231\leftrightarrow 4213\leftrightarrow 1243\leftrightarrow 1423$$
  と一周回ってもないので無理．
• $n=5$はどうせ行けるだろ．120通り全部試せばOK！

って感じになっていたところで時間がなくなりました．答案には$n=4$が不可能で，$n=5$なら$5$を右に持っていくと$n=4$のパターン数が多いバージョンに帰着出来て多分行けるみたいなことまで書いたと思います．

　3への粘着を減らしていれば解ききれたと思われ，反省．6は全く見てません．3完1半（？）です．

---

コンテストはこんな感じで割と上手くいってたらしいです。残りの部分は自分用に秘匿(?)しとくことにします。今年もあればちゃんと結果残したいですねー、まずは予選。

追記：開催が確定していた。
追記2：無事予選を通った。CGCGCG頼みます。