凹多角形の内角の和
凹四角形の内角の和も$2\pi$である
というのを最近知ったので、$n$角形について考えてみました。
小学校で教えてくれればよかったのに。
(証明が小学生にはキツいという向きもあるけど錐体の体積だって証明しないしなあ)
凸多角形
凸$n$角形の内角の和は$(n-2)\pi$である
証明略
凹多角形
凹多角形は、凸多角形から「一辺を共有する凸多角形」をいくつか削り取った図形と考える。
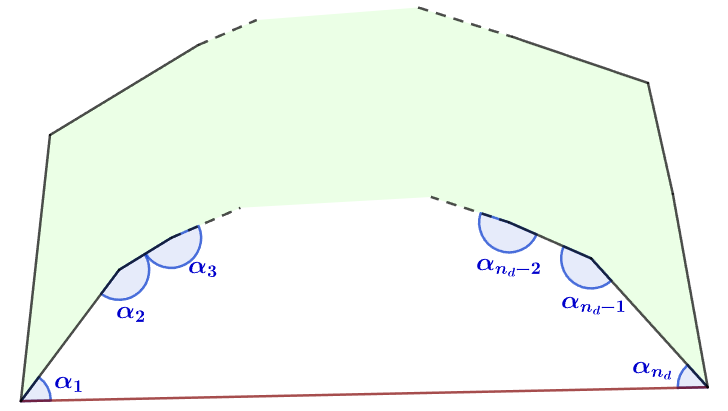
凹$n$角形の内角の和は$(n-2)\pi$である
図形から「辺を共有する多角形」を一つ削り取る操作を考える。
元の多角形を$P_0$,削り取る多角形を$P_d$,できる凹多角形を$P_c$とする。
また、それぞれの角数を$n_0$,$n_d$,$n_c$
内角の和を$D_0$,$D_d$,$D_c$
とする。
$P_0$の内角について次式が成り立つとする。
$D_0=(n_0-2)\pi$
$P_0$と$P_d$は$2$つの頂点を共有しているので、$P_c$の角数は
$n_c=n_0+n_d-2$
$P_d$の内角を、$\alpha_1,\alpha_2,\ldots \alpha_{n_d}$とする($\alpha_1,\alpha_{n_d}$は$P_0$と頂点を共有)と
$P_c$の内角の和は
$$D_c=D_0-(\alpha_1+\alpha_{n_d})+(2\pi-\alpha_2)+(2\pi-\alpha_{3})+\cdots +(2\pi-\alpha_{n_d-1})$$
また、$P_d$の内角の和は
$$D_d=\alpha_1+\alpha_2+\cdots+\alpha_{n_d}$$
辺々足すと
$$D_c+D_d=D_0+2\pi(n_d-2)$$
よって
$$D_c=D_0-D_d+2\pi(n_d-2)$$
$D_0=(n_0-2)\pi$,$D_d=(n_d-2)\pi$であるので
\begin{align}
D_c&=(n_0-2)\pi-(n_d-2)\pi+2\pi(n_d-2) \\
&=(n_0+n_d-4)\pi \\
&=(n_c-2)\pi
\end{align}
以上より、この操作で角数と内角の和の関係は変わらない。
同様の操作を何回行っても同じ議論ができるので
命題が成立する。
矢じり形
凸多角形から、(一辺を共有する)凸多角形を$1$個だけ除いた図形を「矢じり形」とする。
除かれる多角形の内角を$\alpha_{1},\alpha_{2},\ldots,\alpha_{n_d}$とし、元の多角形の内角を$\beta_{1},\beta_{2},\ldots,\beta_{n_0}$とする。
「矢じり形」について、次のような「凸な角」と「凹な角」を考える。
凸な角:$(\beta_1-\alpha_1),\beta_2,\beta_3,\ldots,\beta_{n_0-1},(\beta_{n_0}-\alpha_{n_d})$
凹な角:$\alpha_2,\alpha_3,\dots,\alpha_{n_d-1}$
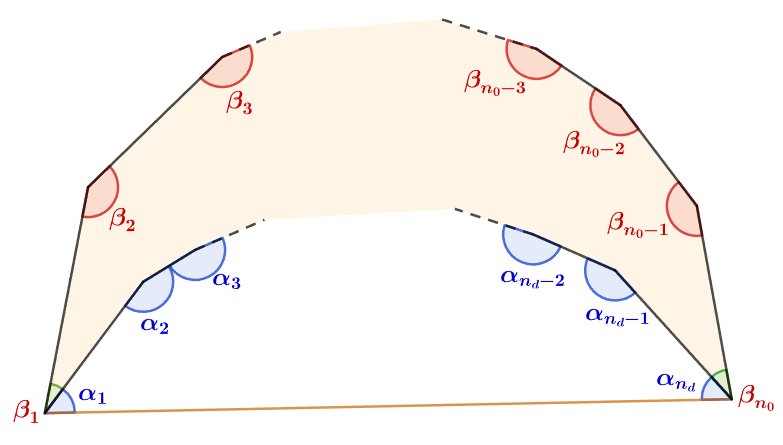
「矢じり形」の凸な角の合計を$T$、凹な角の合計を$P$とすると
$$T=P+(n_0-n_d)\pi$$
とくに$n_0=n_d$のとき
$$T=P$$
$$\beta_{1}+\beta_{2}+\beta_{3}+\cdots+\beta_{n_0}=(n_0-2)\pi$$
$$\alpha_{1}+\alpha_{2}+\alpha_{3}+\cdots+\alpha_{n_d}=(n_d-2)\pi$$
辺々引くと
$$T-P=(n_0-n_d)\pi$$
よって
$$T=P+(n_0-n_d)\pi$$
とくに$n_0=n_d$のとき
$$T=P$$