1
高校数学解説

ax+by=1の整数解（ユークリッドの互除法）

整数,ユークリッドの互除法,1次不定方程式
204
0
$$$$

$ax+by=1$の整数解

はじめに

$ax+by=1$の整数解をみつける方法として、ユークリッドの互除法を利用する方法がある。
高校時代は手順がいまいち理解できていなかったので、自分なりにまとめてみようと思います。

前提と表記

場合分けが面倒なので、特に断りがなければ以下を前提とする。

  • $a \gt 0$、$b \gt 0$
  • $a \gt b$
  • $a$、$b$は互いに素

$ax+by=0$の整数解

$ax+by=1$ の整数解を求める前段階として
$ax+by=0$の整数解について考える

$ax+by=0$ の整数解

方程式
$ax+by=0$
の整数解は、整数 $m$ を用いて
$x=mb$、$y=-ma$
と表すことができる。

$a$、$b$は互いに素なので、$x$は$b$の倍数。よって $x=mb$とおける。
これを方程式に代入すると
$a(mb)+by=0$
$b(ma+y)=0$
$b \neq 0$なので
$ma+y=0$
$y=-ma$

ユークリッドの互除法（表）

step数式1数式2$v$
$1$$a=bq_{1}+r_{1}$$a-bq_{1}=r_{1}$$v_{1}=(1,0)-(0,1)q_1$
$2$$b=r_{1}q_{2}+r_{2}$$b-r_{1}q_{2}=r_{2}$$v_{2}=(0,1)-v_{1}q_{2}$
$3$$r_{1}=r_{2}q_{3}+r_{3}$$r_{1}-r_{2}q_{3}=r_{3}$$v_{3}=v_{1}-v_{2}q_{3}$
$4$$r_{2}=r_{3}q_{4}+r_{4}$$r_{2}-r_{3}q_{4}=r_{4}$$v_{4}=v_{2}-v_{3}q_{4}$
$\vdots$$\vdots$$\vdots$$\vdots$
$k$$r_{k-2}=r_{k-1}q_{k}+r_{k}$$r_{k-2}-r_{k-1}q_{k}=r_{k}$$v_{k}=v_{k-2}-v_{k-1}q_{k}$
$\vdots$$\vdots$$\vdots$$\vdots$
$n$$r_{n-2}=r_{n-1}q_{n}+1$$r_{n-2}-r_{n-1}q_{n}=1$$v_{n}=v_{n-2}-v_{n-1}q_{n}$

表の解説

  • 数式１　互除法の操作。$a$、$b$は互いに素なので最終的なあまりは$1$
  • 数式２　数式１を変形したもの。左辺を「$○a+□b$」のかたちで表すことができれば、
    　　　　最終行が所望の式のかたちになり、１組の整数解を得る。
  • $v$　　　$a=(1,0)$、$b=(0,1)$とおいて数式２を計算したときに$r_k$に相当するベクトルを$v_k$とする。
    　　　　このベクトルは$r_k$を$a$、$b$で表したときの係数とみなせる。

整数解を求める手順

  1. 互除法の操作を実行し、上記の表を埋める。$v_n$を求める。
  2. $v_n=(x_0,y_0)$とすると、$ax_0+by_0=1$が成り立つ。
  3. 一般解を求める。
    \begin{alignat}{2} ax&+by& &=1 \\ -) \ \ \ \ \ ax_0&+by_0& &=1 \\ \hline a(x-x_0)&+b(y-y_0)& &=0 \\ \end{alignat}
    定理１ より
    $x-x_0=mb$
    $y-y_0=-ma$

よって一般解は整数$m$を用いて
　　　$x=x_0+mb$
　　　$y=y_0-ma$
　　　　
※$a$、$b$の大小関係や正負によって、互除法の初期値とベクトルとの関係が変化するので注意

具体例

具体例として$82x+23y=1$の整数解を求める。
$a=82$、$b=23$としてユークリッドの互除法を実行すると

互除法$v$$a$、$b$の式
$82 = 23 \cdot {\color{red}3}+ {\color{blue}13}$$v_{1}=(1,0)-(0,1) \cdot {\color{red}3}=(1,-3)$$a-3b={\color{blue}13}$
$23 = 13 \cdot {\color{red}1}+{\color{blue}10}$$v_{2}=(0,1)-(1,-3) \cdot {\color{red}1}=(-1,4)$$-a+4b={\color{blue}10}$
$13 = 10 \cdot {\color{red}1}+{\color{blue}3}$$v_{3}=(1,-3)-(-1,4) \cdot {\color{red}1}=(2,-7)$$2a-7b={\color{blue}3}$
$10 = 3 \cdot {\color{red}3}+{\color{blue}1}$$v_{4}=(-1,4)-(2,-7) \cdot {\color{red}3}=(-7,25)$$-7a+25b={\color{blue}1}$

上表より$82x+23y=1$の解の１つは$x=-7$、$y=25$
一般解は$m$を整数として
　　　$x=-7+23m$
　　　$y=25-82m$

実践してみると分かるが、ベクトルの計算に必要な情報は各ステップにおける商のみ。
$v_k$を算出するための数式に登場するベクトルは前行を参照・転記すれば良いので
計算は割と簡単。

※途中で出てきた$a$、$b$の式を組み合わせて「$△a+○b=□$」の形の式を新しく作ることができる。
互除法の途中で目的を達成できるときもあるので留意したい。

筆算（試作）

符号やらの関係でミスしがちなので、ミスを減らしつつコンパクトに計算する方法を考えたい。
とりあえず試作。
$ax+by=1$の$a$を$(1,0)$、$b$を$(0,1)$とおいたときに、
互除法の初期値$s1$と$s2$をベクトルで表す。
$s2$から始めて「ベクトルに$(-1) \times \text{互除法の商}$をかける→１つ前のベクトルを加える」操作を繰り返す。

例：$82x+23y=1$
互除法の結果より
$q: {\color{red}3},{\color{red}1},{\color{red}1},{\color{red}3}$
$r:{\color{blue}13},{\color{blue}10},{\color{blue}3},{\color{blue}1}$

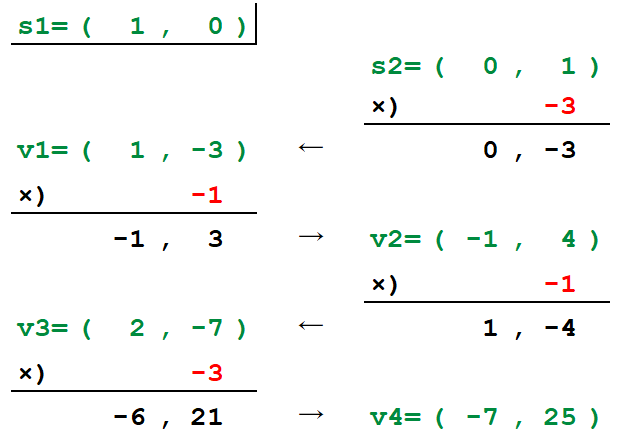筆算 試作 筆算 試作
互除法のStep${\color{#9D5509}2}$の結果を使って
$v{\color{#9D5509}2}=(-1,4)$で、Step${\color{#9D5509}2}$のあまりが${\color{blue}10}$であることから、
「$(x,y)=(-1,4)$は方程式$82x+23y={\color{blue}10}$の整数解の一つである」
みたいなことがいえる。

おわりに

$ax+by=1$ならば
$ax \equiv 1 \pmod b$
$by \equiv 1 \pmod a$

よって今回の計算は、mod演算における逆数っぽいものを求める操作とみることもできそう。
その意味や応用についてはよく分かりませんが、そのうち考えてみたいと思います。

おまけ

計算用のpythonプログラム。 Jupyter Notebook などで実行できる。
最終行の数字を適当に変更して実行すると演習に役立つかも。

      import math
def euclidEx(a,b):
    g=math.gcd(a,b)
    if g>1:
        print('互いに素な数を入力してください')
        return
    if abs(a)<abs(b):
        tmp1=abs(b)
        tmp2=abs(a)
#a=[1,0]、b=[0,1]とおく
#tmp1に相当するベクトル: v1
        if(b<0):
            v1=[0,-1]
        else:
            v1=[0,1]
#tmp2に相当するベクトル
        if(a<0):
            v2=[-1,0]
        else:
            v2=[1,0]
    else:
        tmp1=abs(a)
        tmp2=abs(b)
#a=[1,0]、b=[0,1]とおく
#tmp1に相当するベクトル: v1
        if(a<0):
            v1=[-1,0]
        else:
            v1=[1,0]
#tmp2に相当するベクトル
        if(b<0):
            v2=[0,-1]
        else:
            v2=[0,1]
        
    s=''
    cnt=0
    while tmp2>1:
        q=tmp1//tmp2
        r=tmp1%tmp2
        v=[0,0]
        v[0]=v1[0]-v2[0]*q
        v[1]=v1[1]-v2[1]*q
        s=s+str(tmp1)+'='+str(tmp2)+' × '+str(q)+' + '+str(r)+'        \t'
        s=s+'v_'+str(cnt)+'=' +str(v1)+' - '+str(v2)+ ' ・ ' + str(q)+'\t= '+str(v)+'        \t'
        s=s+polynominal(v,['a','b'])+' = '+ str(r)
        s=s+'\n'
        
        tmp1=tmp2
        tmp2=r
        v1=list(v2)
        v2=list(v)
        
        cnt=cnt+1
        if cnt>100:
            break
    print(s)

def term(keisu,moji,isBegin):
#多項式の中の項を返す（符号、演算子を調整、係数が1のとき係数を削除）
    absK=abs(keisu)  #係数の絶対値
    if absK==1:
         absK=''
    else:
        absK=str(absK)
    if(keisu)>0:        #係数が正
        if isBegin==True:
            ope=''
            sgn=''
        else:
            ope=' + '
            sgn=''
        result=ope+sgn+absK+moji
    elif keisu<0:       #係数が負
        if isBegin==True:
            ope=''
            sgn='-'
        else:
            ope=' - '
            sgn=''
        result=ope+sgn+absK+moji
    else:               #係数が0
        result=''
    return result


def polynominal(k_lst,moji_lst):
#多項式を表す文字列を返す
    result=''
    for i in range(len(k_lst)):
        if i==0:
            result=result+term(k_lst[i],moji_lst[i],True)
        else:
            result=result+term(k_lst[i],moji_lst[i],False)
    return result

#例
euclidEx(131,17)
投稿日：2023年10月13日

この記事を高評価した人

高評価したユーザはいません

この記事に送られたバッジ

バッジはありません。

投稿者

tanu
20
4185

コメント

他の人のコメント

コメントはありません。
読み込み中
tanu
ax+by=1の整数解（ユークリッドの互除法）