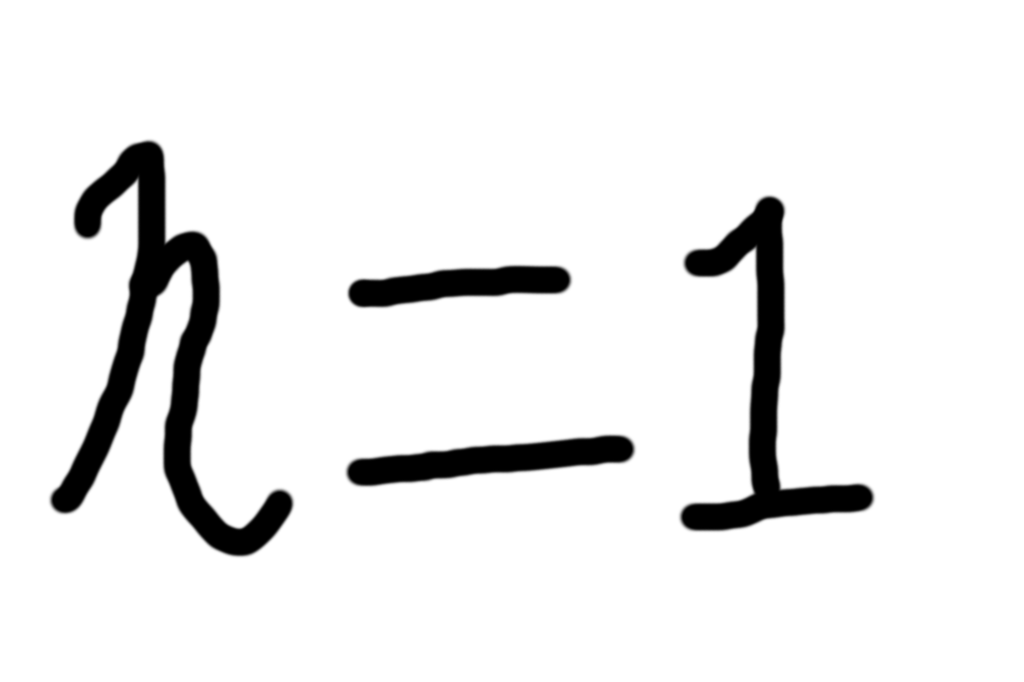点から作る方程式

はじめに

　こんにちはn=1です。今回は、前回投稿した規則的に出力される関数より狭義なときに使える、座標を与えられたときに、与えられた条件に合うn次方程式を出力する関数についてやっていきます。

まずどういうものか

　座標が与えられたそれをn次方程式で表すというのは、$(1,2),(2,4),(3,16)$を通る二次方程式は何、などです。

例

　ではまず簡単な例から考えていきます。式は
$a_{n}=${${1,1,1,\cdots,1,\cdots}$}
として、1はj個あるとします。この式は
$x_{1}(n-2)(n-3)\cdots(n-j)+x_{2}(n-1)(n-3)\cdots(n-j)+x_{3}(n-1)(n-2)\cdots(n-j)+\cdots+x_{j}(n-1)(n-2)(n-3)\cdots(n-(j-1))$
という式で表せるとします。これは1つの項以外は$n-n$になるパターンがすべての項にあるので$x_{m}$はその項の逆数になり、$n=m$として$x_{m}$を考えれば$n$にそれを対応する数を代入したとき成り立ちます。なので
$x_{m}=(\prod_{k=1}^{m-1}(m-k))^{-1}(\prod_{s=m+1}^{j}(m-s))^{-1}=(\prod_{k=1}^{m-1}k)^{-1}(\prod_{s=m+1}^{j}(m-s))^{-1}=(m-1)!^{-1}(\prod_{s=m+1}^{j}s)^{-1}$
となり、また$(\prod_{s=m+1}^{j}(m-s))^{-1}$は普通に考えると$m+1\leq{j}$なので、$-1$で括ると後は$(j-m)!$になるので
$\prod_{s=m+1}^{j}(m-s)=(-1)^{j-(m+1)+1}(1\times2\times3\times\cdots\times(j-m))=(j-m)!(-1)^{j-m}$
になる。そのため$x_{m}$は
$x_{m}=(\prod_{k=1}^{m-1}(m-k))^{-1}(\prod_{s=m+1}^{j}(m-s))^{-1}=\frac{(-1)^{m-j}}{(m-1)!(j-m)!}$
　残りは、$(n-1)(n-2)(n-3)\cdots(n-(m-1))(n-(m+1))\cdots(n-j)$ですが、上の使いまわしで、ポッホハマー記号からの式も使うとできるのでもう総和で表し
$a_{n}=\sum_{m=1}^{j}(\prod_{\alpha=1}^{m-1}(n-\alpha))(\prod_{\beta=m+1}^{j}(n-\beta))x_{m} =\sum_{m=1}^{j}(\frac{\prod_{a=0}^{m-1}(n-a)}{n})(\frac{\prod_{b=0}^{j-m}(n-m-b)}{n-m})x_{m} =\sum_{m=1}^{j}\frac{n!}{(n-m)!n}\frac{(n-m)!}{((n-m)-(j-m))!(n-m)}x_{m} =\sum_{m=1}^{j}\frac{(n-1)!(n-m-1)!(-1)^{m-j}}{(n-m)!(n-j-1)!(m-1)!(j-m)!}=1$
となり、この情報だけだといくつ与えられても1になると分かります。

本題

　では本題の与えられた座標が1のみでない時を求めます。しかし、違う点は$x_{m}$にそのときの値をかけるだけなので
$A_{n}=${$A_{1},A_{2},A_{3},\cdots,A_{j},\cdots$}
$A_{n}=X_{1}(n-2)(n-3)\cdots(n-j)+X_{2}(n-1)(n-3)\cdots(n-j)+\cdots+X_{j}(n-1)(n-2)\cdots(n-(j-1))$
$X_{m}=(\prod_{k=1}^{m-1}(m-k))^{-1}(\prod_{s=m+1}^{j}(m-s))^{-1}A_{m}=\frac{(-1)^{m-j}}{(m-1)!(j-m)!}A_{m}$
$A_{n}=\sum_{m=1}^{j}(\prod_{\alpha=1}^{m-1}(n-\alpha))(\prod_{\beta=m+1}^{j}(n-\beta))X_{m} =\sum_{m=1}^{j}\frac{(n-1)!(n-m-1)!}{(n-m)!(n-j-1)!}X_{m}$
となります。そして、上記の式に条件の値を入れるとその中で恐らく最も次数の少ない式がでます。

この式について

　この式は、自然数が最大の数まで全て出ている時しか使えません。なので、出てない数で途切れさせたり、$X_{m}$から計算すると求まります。
　しかし、n次方程式で表せる式しか正しく表せず、対数や三角関数などは近似しかできません。

例題

↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
↓
　以下は解説です。
　問1は
$X_{1}=1,X_{2}=1,X_{3}=1,X_{4}=1$
$(n-2)(n-3)(n-4)+(n-1)(n-3)(n-4)+(n-1)(n-2)(n-4)+(n-1)(n-2)(n-3)=4n^{3}-30n^{2}+70n-50$
なので$y=4x^{3}-30x^{2}+70x-50$が解の1つです。
　問2は
$X_{1}=1,X_{2}=-\frac{7}{2},X_{4}=\frac{5}{2}$
$A_{n}=(n-2)(n-4)-\frac{7}{2}(n-1)(n-4)+\frac{5}{2}(n-1)(n-2)=4n-1$
なので、$A_{n}=4n-1$が解の1つです。

最後に

　以上で終わりです今回の投稿を見てくださりありがとうございました。