コラッツ予想と２進法

　はじめまして。

　２０年ほど前にコラッツ予想に出会い、Mathematicaを使って自分なりに探究を楽しんできました。

　２００７年頃、どこかの掲示板を通じてコラッツ予想について議論する仲間ができて、自分の考えたことを『コラッツ予想実験室』と題してHPで紹介していたことがありました。

　今でも『コラッツ予想　２進法』で画像検索すると、２００７年に作ったHPに載せてた画像がけっこう上位に出てくるのは、ちょっとした自慢です。(^_^)

　自然数を２進法で表して、それを白黒で表示するというのは、Mathematicaの開発者であるStephen Wolframさんの"A New Kind of Science"という本からの受け売りなんですが、白黒表示すると直感的にわかりやすくて、様々な発見があります。
　
　以下はその２００７年に作ったHPからの転載です。

『コラッツ予想』実験室！                                        
　ここから下は、コラッツ予想に取り組んでいる皆様向けです。（ノウガキさん、ＨＲＳさん、忍さん、頭一族さん、見てくれてる？）注：４者のお名前は当時掲示板で出会ったコラッツ予想探究仲間

　初期値を７として、普通のコラッツ変換をしていくと、　７→２２→１１→３４→１７→　…　→５→１６→８→４→２→１　って、変化していきますよね。それぞれの数を二進数に直して、　０を白、１を黒で表したのが下の図です。
初期値７で普通のコラッツ変換

　でも、これって、”２で割る”っていうのが、”右にずれる”ってことと同じなんだから、いっそのこと、”右につめちゃったやつだけ表示させたら？”ってのが下の図です。
初期値７、２で割れるだけ割って右に詰めたビット列

　で、これだとなんだか大事な情報が抜け落ちてるような気がするんで、”２で割らない”ようにしたのが下の図です。
初期値７、２で割らないで繰り上げてったビット列

　結局、３つとも、ビット列としては同じだってこと、分かってもらえます？
　で、”２で割らない”方法が、いかに興味深いか、次の図を見てもらうといいかも。　初期値を１０２３（２＾１０－１）とすると、こんなになります。
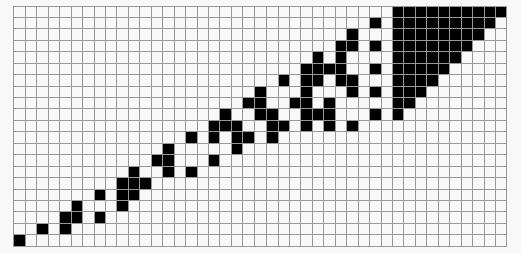初期値1023、２で割らないで繰り上げてったビット列

　ノウガキさん、ＨＲＳさん、いかがですか？　部分的な規則性や、どんなときにビット列が短くなるか、これを見ると　直感的に分かりやすくない？　できれば、Ｍａｔｈｅｍａｔｉｃａでいろいろ実験してみてもらえるといいんだけど。　では、また、ノウガキさんの掲示板で。　最終更新日　２００７１２０６

　と、以上が昔作ったHPからの転載です。

　２進法で表して白黒表示させることのメリット、いろいろあるので、今後この場（Mathlog）を借りてお伝えしていきたいと思います。

　よかったら、下のリンクから『コラッツ予想実験室』が見れますのでご覧ください。おすすめは『２００７１２０８』の『しましましっぽの定理』かな。
http://www7a.biglobe.ne.jp/~kostia/

　ここまで読んでくださった方、ありがとうございました。
　では、また！