2023 ISL G1
以下は僕の解答であり、最善であるとは限りません。逆にいろいろと教えてほしいです。
この記事の目的は個人的なメモでありながら、気になる方々のために出来るだけ思考をわかりやすく説明することです。
よろしくお願いします :)
問題
$ABCDE$は$\angle ABC = \angle AED = 90^{\circ}$を満たす凸五角形である。$CD$の中点は三角形$ABE$の外心であるとする。$O$を三角形$ACD$の外心とする。
直線$AO$は辺$BE$の中点を通ることを示せ。
考察
まずは図を描いてみましょう。
最初は少し難しいけどちょっと頑張れば似たようなのが描ける。
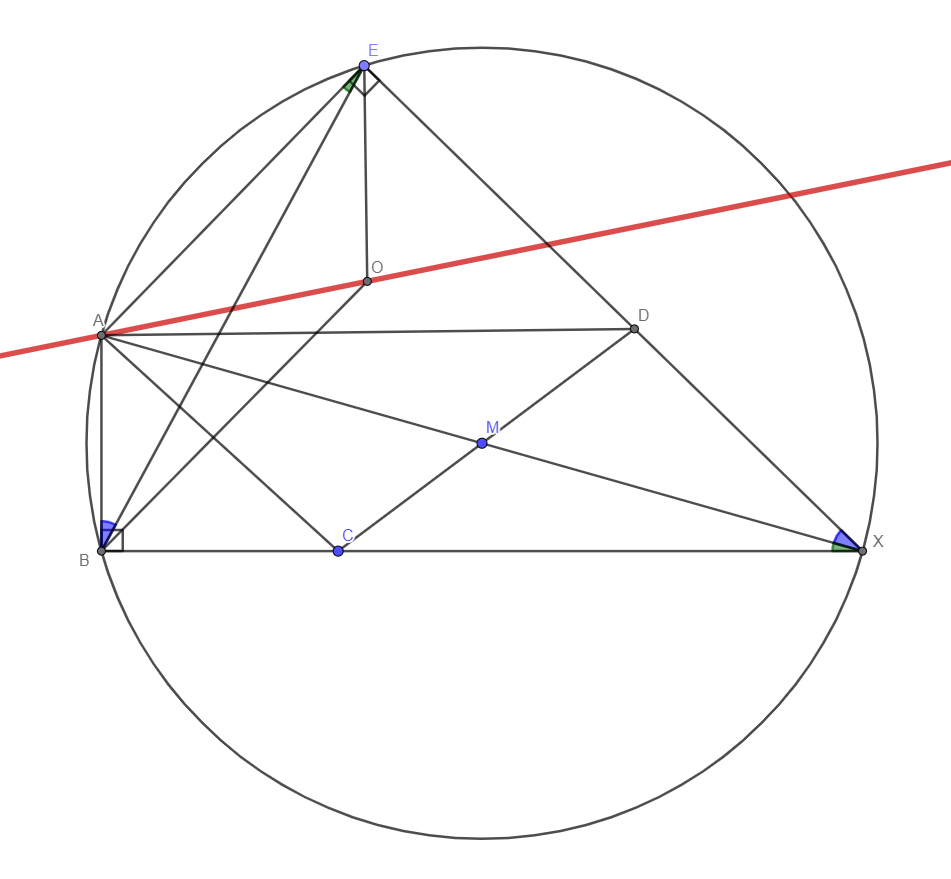Geogebra
中点を通る。。。どうやって示そう。
二等辺三角形を見つけるか平行四辺形の対角線くらいしか思いつかない。
$BE$と$AO$を使う四角形$ABOE$が平行四辺形っぽい。示してみよう。
まずは$90^{\circ}$という角の情報から辺を延長すれば内接四角形が作れる。
すると$CD$の中点$M$は四角形$ABXE$の外心だとわかる。
とくに、直角の情報から$AX$は円の直径である。すると、$AM = MX$がわかる。
与えられた$CM = MD$と組み合わせると、対角線がそれぞれの中点で交わっているので、$ACXD$は平行四辺形である。そのため、辺の平行がわかる。
内接四角形なので角度で遊んでみると、$\angle EXA = \angle EBA, \angle AXB = \angle AEB$がわかる。
でも今のところ点$O$を扱う問題なのに情報が全くない。
$OA = OC = OD$は使い道が無さそう。
じゃあ普通に辺$AC, CD, DA$の二等分線が$O$を通るという情報が使えるかな。
すると、$O$が三角形$EBX$の垂心でありそうなことが浮かんだ。
実際、直線$EO$は$AD$と垂直、つまり$BX$と垂直。
同じように、直線$BO$はACと垂直、つまり$EX$と垂直。
最後に角の情報をいじれば平行がしめされ、四角形$ABOE$が平行四辺形だとわかる。
つまり、対角線がそれぞれの中点で交わる。
何を学ぶか
幾何楽しいね。この問題は中学数学の範囲だけでも解ける！
・図は描きにくくても描ければ結構役立つから挑戦するべき。
・示したいものから逆算？すれば必要な情報がわかってくる。
