積分と級数の部屋で出された積分と級数の合成問題

積分,級数の部屋 　というLINEのオープンチャットにて、
不動点　という人物から級数と積分の合成問題が出されました。
\begin{eqnarray} \lim_{n \rightarrow \infty} n \qty(\log 2 - \sum_{k=1}^n \frac{1}{n+k}) = \alpha \end{eqnarray}
としたとき、$\alpha$を求めよというものでした。
事前に数値計算により答えが0.249999...であることが分かっています。

台形近似を考える

\begin{eqnarray} \sum_{k=1}^n \frac{1}{n+k} &=& \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}}\\ \end{eqnarray}
なので、極限を考えると
\begin{eqnarray} \lim_{n \rightarrow \infty}\frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} &=& \int_0^1 \frac{1}{1+x} \:dx \\&=& \log 2 \end{eqnarray}
これでは問いに答えることができない。
ようは、あの級数が積分結果である$\log2$にどれぐらいの速さで収束するかを考えたときに、$\mathcal O(n^{-1})$の係数はいくらかということ。
今までの区分求積法だとこれは求められない
というのも、
\begin{eqnarray} \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} < &\int_0^1 \frac{1}{1+x} \:dx < \frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{1+\frac{k}{n}}\\ \int_0^1 \frac{1}{1+x} \:dx - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} <& \frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{1+\frac{k}{n}} -\frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} \\ =& \frac{1}{n} \qty(\frac{1}{1+\frac{0}{n}} - \frac{1}{1+\frac{n}{n}}) \\ =& \frac{1}{2n} \end{eqnarray}
だからである。
ここで台形の近似を考えるが、ところで
\begin{eqnarray} \frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{1+\frac{k}{n}} \quad \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} \end{eqnarray}
についてよく見てみる。
画像はコトバンクより 区分求積法

この図2と図3をみて、台形近似について考えると、これらの差の半分
つまり(図3-図2)/2を、図2に足せばいいとわかるね。
なので、
\begin{eqnarray} \frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{1+\frac{k}{n}} - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} =\frac{1}{2n} \end{eqnarray}
より、
\begin{eqnarray} &&\frac{1}{2}\qty(\frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{1+\frac{k}{n}} - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} ) + \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} \\&=& \frac{1}{4n} + \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} \end{eqnarray}
ところで、さっき積分した$\frac{1}{1+x}$を$y$とおいて二階微分すると、
$y''=\frac{1}{(1+x)^3}$になり、これは区間$[0,1]$で正なので、$\frac{1}{1+x}$は区間$[0,1]$において下に凸(区間内の関数上の任意の二点を結ぶ線分が関数の上を通る)と分かるので、台形近似は上からの評価ということになる。
よって、
\begin{eqnarray} \frac{1}{4n} + \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} &>& \int_0^1 \frac{1}{1+x} \:dx \\ \frac{1}{4n} &>& \int_0^1 \frac{1}{1+x} \:dx - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} \\ \frac{1}{4} &>& n\qty(\log 2 - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}}) \end{eqnarray}

じゃあ、下からの評価は？

下からの評価は台形近似ではできない。なぜなら、下に凸だからである。
何とかして下を通さないといけない。
やっぱり接線しかない？うーん。
これはあまりしたくない。なぜなら、$\frac{1}{1+x}$の微分は$-\frac{1}{(1+x)^2}$であり、計算が煩雑になることは容易に想像できる
じゃあどうするか。下から？逆側からの近似？反対？逆？
そうだね。逆関数だね
これを見てもらおう
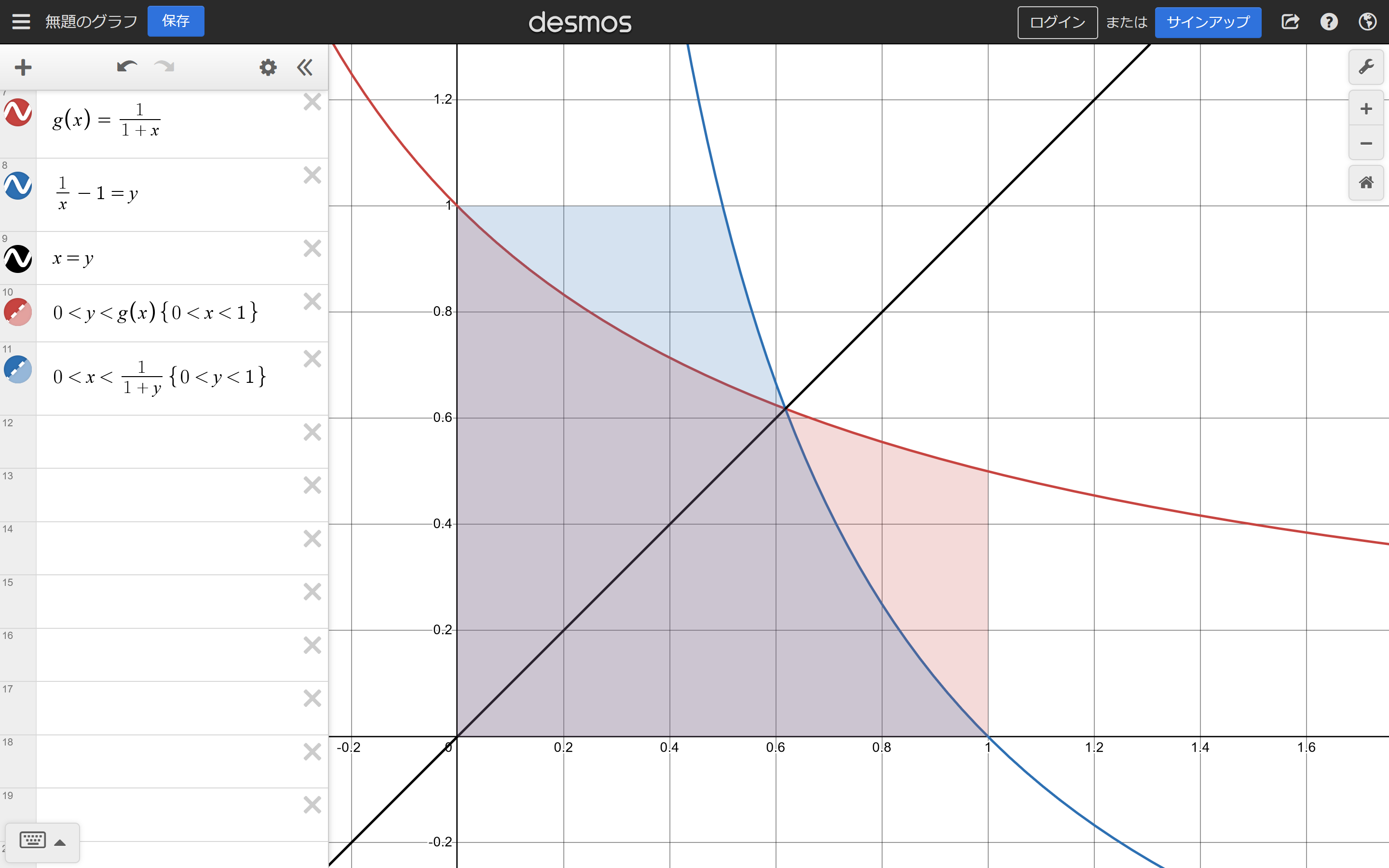desmosで頑張った
赤い曲線は$y=\frac{1}{1+x}$であり、青いほうは$y=\frac{1}{x}-1$だ。そう。逆関数である。
しかもだよ、高校の範囲でちゃんと逆関数は習うし、$y=x$を対称として選対小移動させたものだっていうのもちゃんと習うんだよ！
ってことは、赤い部分の面積と青い部分の面積は一致する。
ここで一番うれしいのはその微分$-\frac{1}{x^2}$が元の関数より簡単になってるっていう点かな。(上に凸になるとかは無い)
一応平行移動させて$\frac{1}{x}$の$[\frac{1}{2},1]$での面積を考える
点$(t,\frac{1}{t})$での接線は$y=-\frac{x}{t^2}+\frac{2}{t}$なので、
区間$[\frac{n+k}{2n},\frac{n+k+1}{2n}]$の台形をこう定める(この変な範囲は区間が$[\frac{1}{2},1]$なのに由来する)
「点$(\frac{n+k}{2n},\frac{2n}{n+k})$で接線を引いたとき、この接線と$x=\frac{n+k}{2n}$と$x=\frac{n+k+1}{2n}$と$y=0$で囲まれる領域」
これを使って台形近似してみよう。

まずこの台形の面積は？

点$(\frac{n+k}{2n},\frac{2n}{n+k})$での接線を求めると$y=-\frac{x}{\qty(\frac{n+k}{2n})^2}+\frac{2}{\frac{n+k}{2n}}$
つまり$y=-\frac{4xn^2}{(n+k)^2}+\frac{4n}{n+k}$
これで$x=\frac{n+k+1}{2n}$の時、
$y= -\frac{2(n+k+1)n}{(n+k)^2}+\frac{4n}{n+k} $
つまり$y=\frac{2n}{n+k}-\frac{2n}{(n+k)^2}$

幅は$\frac{1}{2n}$なので、面積は
\begin{eqnarray} \frac{1}{2}\frac{1}{2n}\qty(\frac{2n}{n+k} + \frac{2n}{n+k}-\frac{2n}{(n+k)^2}) &=& \frac{1}{4n}\qty(\frac{4n}{n+k}-\frac{2n}{(n+k)^2}) \\&=& \frac{1}{n+k}-\frac{1}{2(n+k)^2} \end{eqnarray}
あとは区分求積だね
\begin{eqnarray} \sum_{k=0}^{n-1} \qty(\frac{1}{n+k}-\frac{1}{2(n+k)^2}) &=& \frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{1+\frac{k}{n}} - \frac{1}{2n^2} \sum_{k=0}^{n-1} \frac{1}{1+\qty(\frac{k}{n})^2} \end{eqnarray}
大丈夫か？これ
これは下からの近似のはずなので、
\begin{eqnarray} \int_{\frac{1}{2}}^1 \frac{1}{x} \:dx> \frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{1+\frac{k}{n}} - \frac{1}{2n^2} \sum_{k=0}^{n-1} \frac{1}{1+\qty(\frac{k}{n})^2} \\ \log 2 -\frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}}> \frac{1}{n} \sum_{k=0}^{n-1} \frac{1}{1+\frac{k}{n}} - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} - \frac{1}{2n^2} \sum_{k=0}^{n-1} \frac{1}{1+\qty(\frac{k}{n})^2}\\ \log 2 -\frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}}> \frac{1}{4n}-\frac{1}{2n^2} \sum_{k=0}^{n-1} \frac{1}{1+\qty(\frac{k}{n})^2} \\ n \qty( \log 2 -\frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} ) > \frac{1}{4}-\frac{1}{2n} \sum_{k=0}^{n-1} \frac{1}{1+\qty(\frac{k}{n})^2} \end{eqnarray}
だめじゃん。０に収束しないじゃん。

方針を変える

さすがに厳しいので、何か別の案を考えないといけないう。

というより、上からの評価がうまくいきすぎているので、それをちょっといじってどうにかならんかねこれね。

二次関数を使う

つまり台形近似が線で結んでいるのに対し、２次関数で結ぼうという話。台形近似よりも精度が高いとか。
問題はそれが下からの評価なのかということ。
例えば$\frac{k}{n},\frac{k+1}{n},\frac{k+2}{n}$をとってきたとする。
これを通る二次関数はどうなるかな？
点は$(\frac{k}{n},\frac{n}{n+k}),(\frac{k+1}{n},\frac{n}{n+k+1}),(\frac{k+2}{n},\frac{n}{n+k+2})$である。
平行移動させて$n$で割ると$(-\frac{1}{n},\frac{1}{n+k}),(0,\frac{1}{n+k+1}),(\frac{1}{n},\frac{1}{n+k+2})$
$y=ax^2+bx+c$として、
\begin{eqnarray} \frac{1}{n+k} &=& a\frac{1}{n^2}-\frac{1}{n}b+c \\ \frac{1}{n+k+1} &=& c \\ \frac{1}{n+k+2} &=& a\frac{1}{n^2}+\frac{1}{n}b+c \\ \\ b &=& \frac{n}{2} \qty(\frac{1}{n+k+2} - \frac{1}{n+k}) \\ \frac{1}{n+k} &=& a\frac{1}{n^2}-\frac{1}{2}\qty(\frac{1}{n+k+2} - \frac{1}{n+k}) + \frac{1}{n+k+1} \\ a\frac{1}{n^2} &=& \frac{1}{2}\frac{1}{n+k}+\frac{1}{2}\frac{1}{n+k+2} - \frac{1}{n+k+1} \\ a &=& \frac{1}{2}\frac{n^2}{n+k}+\frac{1}{2}\frac{n^2}{n+k+2} - \frac{n^2}{n+k+1} \\ \\ y &=& \qty(\frac{1}{2}\frac{n^2}{n+k}+\frac{1}{2}\frac{n^2}{n+k+2} - \frac{n^2}{n+k+1}) x^2 + \frac{n}{2} \qty(\frac{1}{n+k+2} - \frac{1}{n+k}) x + \frac{1}{n+k+1} \end{eqnarray}
これを$n$倍して$x$を$x-\frac{k+1}{n}$に変換すると
\begin{eqnarray} y &=& \qty(\frac{1}{2}\frac{n^3}{n+k}+\frac{1}{2}\frac{n^3}{n+k+2} - \frac{n^3}{n+k+1}) \qty(x-\frac{k+1}{n})^2 + \frac{n^2}{2} \qty(\frac{1}{n+k+2} - \frac{1}{n+k}) \qty(x-\frac{k+1}{n}) + \frac{n}{n+k+1} \\ y &=& \qty(\frac{1}{2}\frac{n^3}{n+k}+\frac{1}{2}\frac{n^3}{n+k+2} - \frac{n^3}{n+k+1}) x^2 - \qty(\frac{n^2(k+1)}{n+k}+\frac{n^2(k+1)}{n+k+2} - \frac{2n^2(k+1)}{n+k+1}) x + \qty(\frac{1}{2}\frac{n(k+1)^2}{n+k}+\frac{1}{2}\frac{n(k+1)^2}{n+k+2} - \frac{n(k+1)^2}{n+k+1}) + \frac{n^2}{2} \qty(\frac{1}{n+k+2} - \frac{1}{n+k}) x - \frac{n(k+1)}{2} \qty(\frac{1}{n+k+2} - \frac{1}{n+k}) + \frac{n}{n+k+1} \\ y &=& \qty(\frac{1}{2}\frac{n^3}{n+k}+\frac{1}{2}\frac{n^3}{n+k+2} - \frac{n^3}{n+k+1}) x^2 - \qty(\frac{n^2(k+\frac{3}{2})}{n+k}+\frac{n^2(k+\frac{1}{2})}{n+k+2} - \frac{2n^2(k+1)}{n+k+1}) x + \qty(\frac{1}{2}\frac{n(k+1)(k+2)}{n+k}+\frac{1}{2}\frac{nk(k+1)}{n+k+2} -\frac{n(k+1)^2-n}{n+k+1}) \\ \\ \end{eqnarray}
問題はこれが区間$[\frac{k}{n},\frac{k+2}{n}]$で、$y=\frac{1}{1+x}$より下かどうか。
この式を$f(x)$として、$\frac{1}{1+x}-f(x)$を考える。
$1+x$をかけると、$1-(1+x)f(x)$である。これは3次関数になる。
また、点$(\frac{k}{n},0),(\frac{k+1}{n},0),(\frac{k+2}{n},0)$を通る。
この3次関数の3次の項の係数は
\begin{eqnarray} -\frac{1}{2}\frac{n^3}{n+k} -\frac{1}{2}\frac{n^3}{n+k+2} +\frac{n^3}{n+k+1} &=& \frac{n^3}{2} \qty(\frac{2}{n+k+1}-\frac{1}{n+k}-\frac{1}{n+k+2}) \\ &=& \frac{n^3}{2} \qty(\frac{2}{n+k+1}-\frac{2n+2k+2}{(n+k)(n+k+2)}) \\ &=& \frac{n^3}{2} \qty(\frac{2n+2k+2}{(n+k+1)^2}-\frac{2n+2k+2}{(n+k-1)^2-1}) \\&<&0 \end{eqnarray}
より負なので

と分かります(いや2次関数全部計算しやんくてよかったんかーい)
なので区間$[\frac{k+1}{n},\frac{k+2}{n}]$では正になっている。つまり$\frac{1}{1+x}$のほうが上を通っているのでヨシ！

では、短冊一つの面積を求めていきます。 　

短冊の面積

これは6分の1公式の使いどころですね
点$(\frac{k+1}{n},\frac{n}{n+k+1}),(\frac{k+2}{n},\frac{n}{n+k+2})$を通る直線との囲まれた面積は
\begin{eqnarray} &&\frac{1}{6}\qty( \frac{1}{2}\frac{n^3}{n+k} +\frac{1}{2}\frac{n^3}{n+k+2} -\frac{n^3}{n+k+1} ) \qty(\frac{k+2}{n}-\frac{k+1}{n})^3 \\ &=& \frac{1}{12}\frac{1}{n+k} +\frac{1}{12}\frac{1}{n+k+2} -\frac{1}{6}\frac{1}{n+k+1} \\ &=& \frac{1}{12}\frac{1}{n(1+\frac{k}{n})} +\frac{1}{12}\frac{1}{n(1+\frac{k+2}{n})} -\frac{1}{6}\frac{1}{n(1+\frac{k+1}{n})} \\ &=& \frac{1}{n}\qty( \frac{1}{12}\frac{1}{1+\frac{k}{n}} +\frac{1}{12}\frac{1}{1+\frac{k+2}{n}} -\frac{1}{6}\frac{1}{1+\frac{k+1}{n}} ) \\ \end{eqnarray}
なのでこれを台形の面積から引けばいいと
\begin{eqnarray} \frac{1}{2n}\qty(\frac{n}{n+k+1} + \frac{n}{n+k+2}) &=& \frac{1}{n}\qty(\frac{1}{2}\frac{1}{1+\frac{k+1}{n}} + \frac{1}{2}\frac{1}{1+\frac{k+2}{n}}) \end{eqnarray}
引くと、
\begin{eqnarray} &&\frac{1}{n}\qty(\frac{1}{2}\frac{1}{1+\frac{k+1}{n}} + \frac{1}{2}\frac{1}{1+\frac{k+2}{n}}) - \frac{1}{n}\qty( \frac{1}{12}\frac{1}{1+\frac{k}{n}} +\frac{1}{12}\frac{1}{1+\frac{k+2}{n}} -\frac{1}{6}\frac{1}{1+\frac{k+1}{n}}) \\&=& \frac{1}{n} \qty( \frac{1}{2}\frac{1}{1+\frac{k+1}{n}} +\frac{1}{2}\frac{1}{1+\frac{k+2}{n}} -\frac{1}{12}\frac{1}{1+\frac{k}{n}} -\frac{1}{12}\frac{1}{1+\frac{k+2}{n}} +\frac{1}{6}\frac{1}{1+\frac{k+1}{n}} ) \\&=& \frac{1}{n} \qty( -\frac{1}{12}\frac{1}{1+\frac{k}{n}} +\frac{2}{3}\frac{1}{1+\frac{k+1}{n}} +\frac{5}{12}\frac{1}{1+\frac{k+2}{n}} ) \end{eqnarray}
これ範囲が$[\frac{k+1}{n},\frac{k+2}{n}]$なので、$k\rightarrow k-1$として
\begin{eqnarray} \frac{1}{n} \qty( -\frac{1}{12}\frac{1}{1+\frac{k-1}{n}} +\frac{8}{12}\frac{1}{1+\frac{k}{n}} +\frac{5}{12}\frac{1}{1+\frac{k+1}{n}} ) \end{eqnarray}
としておきましょう
これを足すのですが、$(k=0 \sim n-1)$
イメージはこんな感じです
\begin{eqnarray} &&-1,~~~8,~~~5\\ &&~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\cdots \\ &&~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow \\ &&-1,~~~7,~12,~12,~12,~12,\cdots \\ &&-1,~~~0,~~~1,~~~2,~~~3,~~~4,\cdots \quad\quad(\leftarrow k) \end{eqnarray}
ここから
\begin{eqnarray} \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} \end{eqnarray}
を引くので、
\begin{eqnarray} &&-1,~~~8,~~~5\\ &&~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\ddots \\ &&~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow \\ &&-1,~~~7,~~~0,~~~0,~~~0,~~~0,\cdots \\ \\ \\ \\ &&~~~\ddots\\ &&-1,~~~8,~~~5\\ &&~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ &&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~,-1,~~~8,~~~5\\ \\ &&~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow~~~\downarrow \\ &&~~~~~~0,~~~0,~~~0,~~~0,~~~0,~~~0,~~~1,-7 \end{eqnarray}
結局残るのは
\begin{eqnarray} &&\frac{1}{n} \qty(-\frac{1}{12}\frac{1}{1-\frac{1}{n}}+\frac{7}{12}+\frac{1}{12}\frac{1}{1+\frac{n-1}{n}}-\frac{7}{24}) \\&=&\frac{1}{n} \qty(-\frac{1}{12}\frac{n}{n-1}+\frac{7}{24}+\frac{1}{12}\frac{n}{2n-1}) \\&=&\frac{1}{n} \qty(\frac{7}{24}+\frac{1}{12}\qty(\frac{n}{2n-1}-\frac{n}{n-1})) \\&=&\frac{1}{n} \qty(\frac{7}{24}+\frac{1}{12}\qty(\frac{n-\frac{1}{2}+\frac{1}{2}}{2n-1}-\frac{n-1+1}{n-1})) \\&=&\frac{1}{n} \qty(\frac{7}{24}+\frac{1}{12}\qty(\frac{1}{2}+\frac{\frac{1}{2}}{2n-1}-1-\frac{1}{n-1})) \\&=&\frac{1}{n} \qty(\frac{7}{24}+\frac{1}{12}\qty(-\frac{1}{2}+\frac{\frac{1}{2}}{2n-1}-\frac{1}{n-1})) \\&=&\frac{1}{n} \qty(\frac{6}{24}+\frac{1}{12}\qty(\frac{\frac{1}{2}}{2n-1}-\frac{1}{n-1})) \\&=&\frac{1}{n} \qty(\frac{1}{4}-\frac{1}{12}\qty(\frac{1}{n-1}-\frac{\frac{1}{2}}{2n-1})) \\&=&\frac{1}{4n}-\frac{1}{12n}\qty(\frac{1}{n-1}-\frac{\frac{1}{2}}{2n-1}) \end{eqnarray}

これはいったい何をしてるの？

2次関数で近似した短冊の一つの面積がこう表されることを計算した。
(範囲は$[\frac{k}{n},\frac{k+1}{n}]$)
\begin{eqnarray} \frac{1}{n} \qty( -\frac{1}{12}\frac{1}{1+\frac{k-1}{n}} +\frac{8}{12}\frac{1}{1+\frac{k}{n}} +\frac{5}{12}\frac{1}{1+\frac{k+1}{n}} ) \end{eqnarray}
これを$k=0 \sim n-1$まで足せば関数$y=\frac{1}{1+x}$の$[0,1]$の積分を下から抑えられる
つまり、
\begin{eqnarray} \int_{0}^{1} \frac{1}{1+x} \: dx > \sum_{k=0}^{n-1} \frac{1}{n} \qty( -\frac{1}{12}\frac{1}{1+\frac{k-1}{n}} +\frac{8}{12}\frac{1}{1+\frac{k}{n}} +\frac{5}{12}\frac{1}{1+\frac{k+1}{n}} ) \end{eqnarray}
ここから
\begin{eqnarray} \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} \end{eqnarray}
を引く
\begin{eqnarray} \int_{0}^{1} \frac{1}{1+x} \: dx - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} &>& \frac{1}{n} \sum_{k=0}^{n-1} \qty( -\frac{1}{12}\frac{1}{1+\frac{k-1}{n}} +\frac{8}{12}\frac{1}{1+\frac{k}{n}} +\frac{5}{12}\frac{1}{1+\frac{k+1}{n}} ) - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} \end{eqnarray}
この右辺を計算した結果が上記に書いてある
\begin{eqnarray} \int_{0}^{1} \frac{1}{1+x} \: dx - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} &>& \frac{1}{4n}-\frac{1}{12n}\qty(\frac{1}{n-1}-\frac{\frac{1}{2}}{2n-1}) \end{eqnarray}
$n$倍して
\begin{eqnarray} n \qty( \int_{0}^{1} \frac{1}{1+x} \: dx - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}} ) &>& \frac{1}{4}-\frac{1}{12}\qty(\frac{1}{n-1}-\frac{\frac{1}{2}}{2n-1}) \end{eqnarray}

きたあああああああああああああああ！！！！！！！！
ということで台形近似と二次関数の近似で上下からの評価ができました

はさみうちの原理より

\begin{eqnarray} \frac{1}{4} &>& n\qty(\log 2 - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}}) > \frac{1}{4}-\frac{1}{12}\qty(\frac{1}{n-1}-\frac{\frac{1}{2}}{2n-1}) \end{eqnarray}
なので、極限を付けて
\begin{eqnarray} \frac{1}{4} &>& \lim_{n \rightarrow \infty} n\qty(\log 2 - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}}) > \lim_{n \rightarrow \infty} \qty( \frac{1}{4}-\frac{1}{12}\qty(\frac{1}{n-1}-\frac{\frac{1}{2}}{2n-1})) \end{eqnarray}
ここで、左辺は当然$\frac{1}{4}$で、右辺も$\frac{1}{4}$に収束するので
はさみうちの原理により
\begin{eqnarray} \lim_{n \rightarrow \infty} n\qty(\log 2 - \frac{1}{n} \sum_{k=1}^n \frac{1}{1+\frac{k}{n}}) = \frac{1}{4} \end{eqnarray}

おわり

むずかったね
特に下からの評価をどうするとよいのか結構悩みました
高校範囲で解けることが分かりました。
数値計算のおかげで方針が間違っているとか、答えがあっているとか分かった。
台形近似や二次関数での近似(kinda シンプソンの公式)は$\mathcal O(n^{-1})$のオーダーぐらいまでわかる。
ではまた(｡･ω･)ﾉﾞ