【導出】母線の描く曲面の面積

まえがき

こんにちは、高3のぱぺです。
今年のハロウィーンの雨、すごかったですね。普通に学校帰りに直撃して風邪ひきそうだった。

本題

今回導出したものが以下です。

母線の描く曲面の面積

導出

$P_t$の座標を$\left(x(t),y(t),z(t)\right)$ とする。また、$\alpha\leq w \leq \beta$ において、$\alpha\leq t\leq w$ で線分$\text{OP}$ が描く曲面の面積$S(w)$ とする。このとき、$S(\alpha)=0$.
ここで、$\alpha\leq w<\beta$ において、$0<\Delta{w}<<\beta-w$ となる $\Delta{w}$ を考える。
$S(w+\Delta{w})-S(w)=\triangle{\text{O}\text{P}_{w}\text{P}_{w+\Delta{w}}} \quad -①$

$S(w-\Delta{w})-S(w)=-\triangle{\text{O}\text{P}_{w}\text{P}_{w-\Delta{w}}} \quad -②$

ここで、以下を用いる。

$ $

$\displaystyle \overrightarrow{\text{OP}_{w}}=\begin{pmatrix}x(w) \\ y(w) \\ z(w)\end{pmatrix} \;,\quad \overrightarrow{\text{OP}_{w+\Delta{w}}}=\begin{pmatrix}x(t+\Delta{w}) \\ y(w+\Delta{w}) \\ z(w+\Delta{w})\end{pmatrix} $ であることから、以下 $f(w)=f, \; f(w+\Delta{w})=\overline{f}$ と略記して

$ $

\begin{aligned} \triangle{\text{O}\text{P}_{w}\text{P}_{w+\Delta{w}}} &=\frac{1}{2}\sqrt{\left(x\overline{y}-\overline{x}y\right)^2+\left(y\overline{z}-\overline{y}z\right)^2+\left(z\overline{x}-\overline{z}x\right)^2}\\ \\ &= \Delta{w} \cdot \frac{1}{2} \sqrt{ \left(x\cdot\frac{\overline{y}-y}{\Delta{w}}-y\cdot\frac{\overline{x}-x}{\Delta{w}}\right)^2+ \left(y\cdot\frac{\overline{z}-z}{\Delta{w}}-z\cdot\frac{\overline{y}-y}{\Delta{w}}\right)^2+ \left(z\cdot\frac{\overline{x}-x}{\Delta{w}}-x\cdot\frac{\overline{z}-z}{\Delta{w}}\right)^2 }\\ \end{aligned}

これを$①$ に代入して整理すると (見やすさのため式番号は前に振っている。)

$$ ①' \cdots (\Delta{w}>0)\quad \frac{S(w+\Delta{w})-S(w)}{\Delta{w}}=\frac{1}{2} \sqrt{ \left(x(w)\cdot\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}-y(w)\cdot\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}\right)^2+ \left(y(w)\cdot\frac{z(w+\Delta{w})-z(w)}{\Delta{w}}-z(w)\cdot\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}\right)^2+ \left(z(w)\cdot\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}-x(w)\cdot\frac{z(w+\Delta{w})-z(w)}{\Delta{w}}\right)^2 }$$

これは$②$についても(多分)同じことが言える。(見やすさのため式番号は前に振っている。)

$$ ②' \cdots (\Delta{w}>0)\quad \frac{S(w-\Delta{w})-S(w)}{-\Delta{w}}=\frac{1}{2} \sqrt{ \left(x(w)\cdot\frac{y(w-\Delta{w})-y(w)}{-\Delta{w}}-y(w)\cdot\frac{x(w-\Delta{w})-x(w)}{-\Delta{w}}\right)^2+ \left(y(w)\cdot\frac{z(w-\Delta{w})-z(w)}{-\Delta{w}}-z(w)\cdot\frac{y(w-\Delta{w})-y(w)}{-\Delta{w}}\right)^2+ \left(z(w)\cdot\frac{x(w-\Delta{w})-x(w)}{-\Delta{w}}-x(w)\cdot\frac{z(w-\Delta{w})-z(w)}{-\Delta{w}}\right)^2 }$$

・$②'$ 左辺の負符号は、$②$の両辺を$-\Delta{w}$ で割ったことにより右辺の負符号が移ったもの。
・$②'$ 右辺の分数部分の分母は次のようにして生じている。
\begin{aligned} & \left(x(w)\cdot\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}-y(w)\cdot\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}\right)^2 \\ \\ =& \left\{(-1)\cdot \left\{x(w)\cdot\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}-y(w)\cdot\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}\right\}\right\}^2 \\ \\ =& \left(x(w)\cdot\frac{y(w+\Delta{w})-y(w)}{-\Delta{w}}-y(w)\cdot\frac{x(w+\Delta{w})-x(w)}{-\Delta{w}}\right)^2 \\ \end{aligned}

$ $
$ $

さらに、 $②'$ は$\Delta{w}>0$ が前提であったが、$①'$ と同じ形を作りたい。できれば $-\Delta{w}$ を新しい「負の変化量」としておきたい。
とはいえ、$\Delta{w}$ の記号はそのまま使いたいので、ややこしくはなるが、

$-\Delta{w}\; (\Delta{w}>0) \rightarrow \Delta{w} \; (<0)$ と置き換えることにする。
(見やすさのため式番号は前に振っている。)

$$②'' \cdots (\Delta{w}<0)\quad \frac{S(w+\Delta{w})-S(w)}{\Delta{w}}= \frac{1}{2} \sqrt{ \left(x(w)\cdot\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}-y(w)\cdot\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}\right)^2+ \left(y(w)\cdot\frac{z(w+\Delta{w})-z(w)}{\Delta{w}}-z(w)\cdot\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}\right)^2+ \left(z(w)\cdot\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}-x(w)\cdot\frac{z(w+\Delta{w})-z(w)}{\Delta{w}}\right)^2}$$

$ $
$ $

$①', ②''$ より、$\Delta{w}\neq0$ において、
$$③ \cdots \frac{S(w+\Delta{w})-S(w)}{\Delta{w}}= \frac{1}{2} \sqrt{ \left(x(w)\cdot\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}-y(w)\cdot\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}\right)^2+ \left(y(w)\cdot\frac{z(w+\Delta{w})-z(w)}{\Delta{w}}-z(w)\cdot\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}\right)^2+ \left(z(w)\cdot\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}-x(w)\cdot\frac{z(w+\Delta{w})-z(w)}{\Delta{w}}\right)^2}$$
(見やすさのため式番号は前に振っている。)

$ $

両辺について、$\Delta{w}\rightarrow 0$ の極限をとる。
$$\lim_{\Delta{w}\rightarrow0}\frac{S(w+\Delta{w})-S(w)}{\Delta{w}}=S'(w)$$
$$\lim_{\Delta{w}\rightarrow0}\frac{x(w+\Delta{w})-x(w)}{\Delta{w}}=x'(w)$$
$$\lim_{\Delta{w}\rightarrow0}\frac{y(w+\Delta{w})-y(w)}{\Delta{w}}=y'(w)$$
$$\lim_{\Delta{w}\rightarrow0}\frac{z(w+\Delta{w})-z(w)}{\Delta{w}}=z'(w)$$
を用いて、$③$ は次のように変形できる。

$$S'(w)=\frac{1}{2} \sqrt{ \left\{x(w)y'(w)-x'(w)y(w)\right\}^2+ \left\{y(w)z'(w)-y'(w)z(w)\right\}^2+ \left\{z(w)x'(w)-z'(w)x(w)\right\}^2 } \quad -④$$

略記して、見やすいように整理すると

$$④\cdots S'=\frac{1}{2} \sqrt{ \left(x'y-y'x\right)^2+ \left(y'z-z'y\right)^2+ \left(z'x-x'z\right)^2 }$$

これを$\alpha$ から $\beta$ の間で定積分する。

\begin{aligned} S&=S(\beta) \\ &=S(\beta)-S(\alpha) \quad (\because S(\alpha)=0) \\ &=\int_{\alpha}^{\beta} S'(t) \;dt \\ &=\frac{1}{2}\int_{\alpha}^{\beta} \sqrt{\left(x'y-y'x\right)^2+\left(y'z-z'y\right)^2+\left(z'x-x'z\right)^2} \; dt \end{aligned}

$ $
$ $
$ $
$ $
$ $

使ってみよう

1.　底面の半径$r$, 高さ$h$ の直円錐の側面積

$\begin{cases} x(t)=r\sin{t}\\ y(t)=r\cos{t}\\ z(t)=h \end{cases} \quad \left(0\leq t \leq 2π\right)$

とすると

\begin{cases} x'(t)&=r\cos{t} \\ y'(t)&=-r\sin{t} \\ z'(t)&=0 \end{cases}

これを用いて
\begin{aligned} &\left(x'y-y'x\right)^2 = \left\{r\cos{t}\cdot r\cos{t}-\left(-r\sin{t}\right)\cdot r\sin{t}\right\}^2 = r^4 \\ &\left(y'z-z'y\right)^2 = \left\{\left(-r\sin{t}\right)\cdot h - 0\cdot r\cos{t}\right\}^2=r^2h^2\sin^2{t} \\ &\left(z'x-x'z\right)^2=\left\{0\cdot r\sin{t} -r\cos{t}\cdot h\right\}^2=r^2h^2\cos^2{t} \\ \\ &\therefore \left(x'y-y'x\right)^2+\left(y'z-z'y\right)^2+\left(z'x-x'z\right)^2 \\ &= r^4+r^2h^2\sin^2{t}+r^2h^2\cos^2{t} \\ &=r^2\left(r^2+h^2\right) \end{aligned}

したがって、
\begin{aligned} S&=\frac{1}{2}\int_{\alpha}^{\beta} \sqrt{\left(x'y-y'x\right)^2+\left(y'z-z'y\right)^2+\left(z'x-x'z\right)^2} \; dt\\ &=\frac{1}{2}\int_{0}^{2π} \sqrt{r^2\left(r^2+h^2\right)} \; dt \\ &=πr\sqrt{r^2+h^2} \end{aligned}

母線$R=\sqrt{r^2+h^2}$ で直円錐の側面積 $S=πrR$ だったはずなので、確かに合っています。

2.　放物線の一部

放物線の一部 $y=x^2+2, \; -1\leq x \leq 1, \; z=0$ 上の点$\text{P}(t,t^2+2,0)$ と $\text{O}(0,0,1)$ を結ぶ線分$\text{OP}$ の描く曲面$C$を考える

曲面$C$

$\begin{cases} x(t)=t\\ y(t)=t^2-1\\ z(t)=-1 \end{cases} \quad \left(-1\leq t \leq 1\right)$

とすると

\begin{cases} x'(t)&=1 \\ y'(t)&=2t \\ z'(t)&=0 \end{cases}

これを用いて
\begin{aligned} &\left(x'y-y'x\right)^2 = \left\{1\cdot\left(t^2-1\right)-2t\cdot t\right\}^2 = \left(t^2+1\right)^2 \\ &\left(y'z-z'y\right)^2 = \left\{2t\cdot\left(-1\right) - 0\cdot \left(t^2-1\right)\right\}^2=4t^2 \\ &\left(z'x-x'z\right)^2=\left\{0\cdot t -1\cdot \left(-1\right)\right\}^2=1 \\ \\ &\therefore \left(x'y-y'x\right)^2+\left(y'z-z'y\right)^2+\left(z'x-x'z\right)^2 \\ &= \left(t^2+1\right)^2+4t^2+1 \\ &= \left(t^2+3\right)^2-7 \end{aligned}

$ $

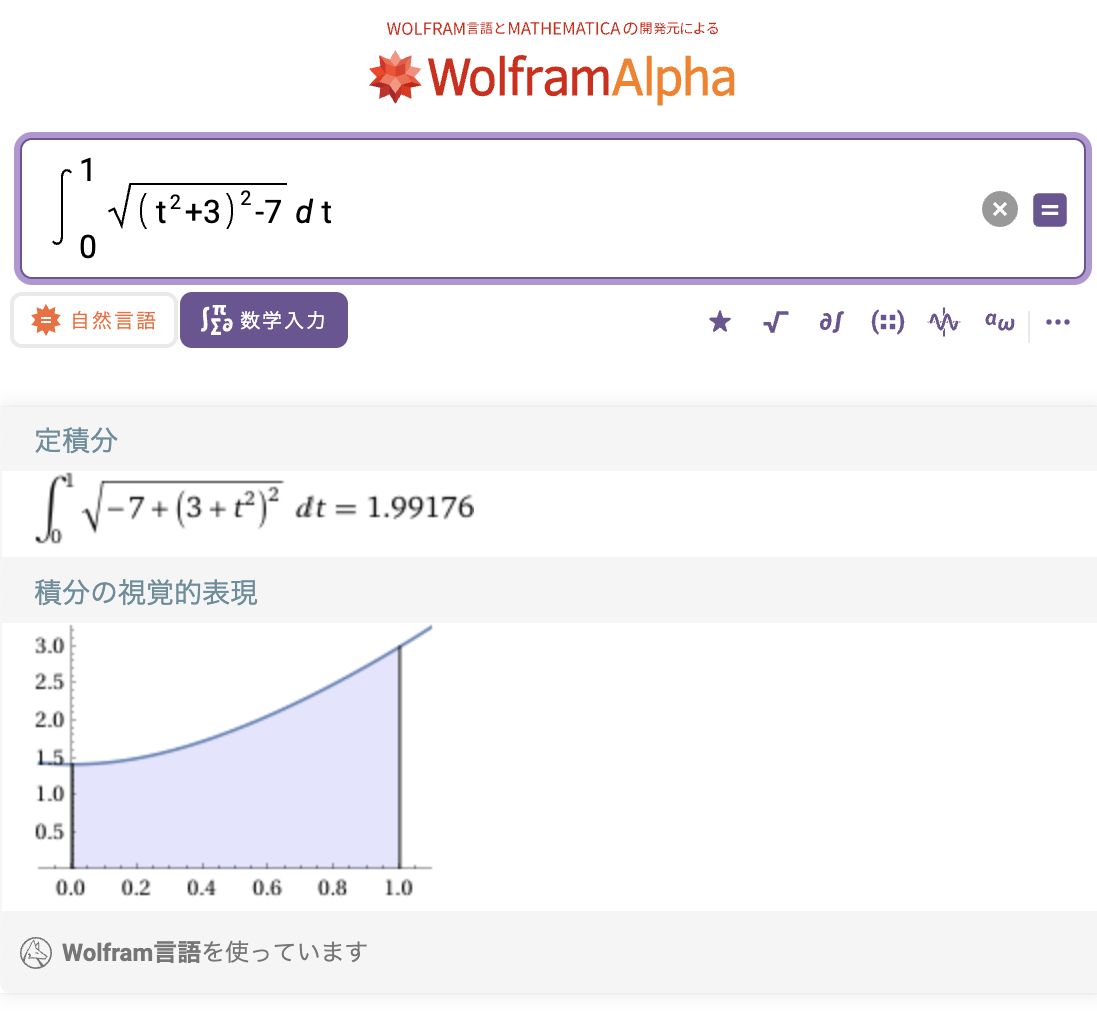
\begin{aligned} S&=\frac{1}{2}\int_{-1}^{1} \sqrt{\left(t^2+3\right)^2-7} \; dt \\ \\ &=\int_{0}^{1} \sqrt{\left(t^2+3\right)^2-7} \; dt \\ \\ &\approx 1.99176 \end{aligned}

ChatGPTに聞いたら、積分$\displaystyle \int_{0}^{1} \sqrt{\left(t^2+3\right)^2-7} \; dt $ は楕円積分を要し、結果初等関数では表せないとのことなので、ちょっとWolfram先生に数値計算してもらいました。(ChatGPTは数値計算を間違え続けていたのでWolframさんを採用。)
Wolfram先生！

3.　線分

簡単のため、$x=z=1,-1\leq y\leq 1$ を考えます。
線分 $x=z=1\; \text{and}\;-1\leq y\leq 1$
$\begin{cases} x(t)=1 \\ y(t)=t \\ z(t)=1 \end{cases} \quad \left(-1\leq t\leq 1\right)$

とすると、

$\begin{cases} x'(t)=0 \\ y'(t)=1 \\ z'(t)=0 \end{cases}$

これを用いて
\begin{aligned} &\left(x'y-y'x\right)^2 = \left\{0\cdot t-1\cdot 1\right\}^2 = 1 \\ &\left(y'z-z'y\right)^2 = \left\{1\cdot1 - 0\cdot t\right\}^2=1 \\ &\left(z'x-x'z\right)^2=\left\{0\cdot 1 -0\cdot 1\right\}^2=0 \\ \\ &\therefore \left(x'y-y'x\right)^2+\left(y'z-z'y\right)^2+\left(z'x-x'z\right)^2 \\ &= 1+1+0 \\ &= 2 \end{aligned}

$ $

\begin{aligned} S&=\frac{1}{2}\int_{-1}^{1} \sqrt{2} \; dt \\ \\ &=\sqrt{2} \end{aligned}

検算すると、$\displaystyle \frac{1}{2}\cdot 2 \cdot \sqrt{2}=\sqrt{2}$ で、確かに合っています。

$ $
$ $
$ $
$ $

関連する定理：　ガウスグリーンの定理

先ほどの定理1で $\text{P}$ が原点$\text{O}$ を含む平面 $z=0$ 上を動くときを考えます。
$z(t)=0, \; z'(t)=0$ であることから、$\left(y'z-z'y\right)^2+\left(z'x-x'z\right)^2=0$
従って、次が得られます。

これはガウスグリーンの定理にかなり近いものになっていますね。

$ $

この2つには微妙に違いがあります。
定理2 (ガウスグリーンの定理) では時計回りに動径が移動した部分を負の面積として計上するのですが、定理1'では正の面積として計上しているんですよね。

元々 定理1 では空間上の曲面を考えていたために、同じ領域を線分$\text{OP}$ が通過するケースを考えていないんですよね。例を出しましょう。

$ $
$ $

例：$\left(x-2\right)^2+y^2=1,z=0$

$\left(x-2\right)^2+y^2=1,z=0$

1. ガウスグリーンの定理

ガウスグリーンの定理では：
$\begin{cases} x=2+\cos{t} \\ y=\sin{t} \end{cases}$
を用いて、
\begin{aligned}x\cdot y'-y\cdot x' &=\left(2+\cos{t}\right)\cdot\cos{t}-\sin{t}\cdot\left(-\sin{t}\right) \\ &=1+2\cos{t} \\ \end{aligned}
\begin{aligned} \therefore \quad S&=\int_{0}^{2π} \frac{1}{2}\left\{1+2\cos{t}\right\} \; dt \\ &=\frac{1}{2}\left[t+2\sin{t}\right]_{0}^{2π}\\ &=π \end{aligned}
これはちょうど円の面積となりますね。

2. 定理1'

定理1'では：
$\begin{cases} x=2+\cos{t} \\ y=\sin{t} \end{cases}$
を用いて、
\begin{aligned}x\cdot y'-y\cdot x' &=\left(2+\cos{t}\right)\cdot\cos{t}-\sin{t}\cdot\left(-\sin{t}\right) \\ &=1+2\cos{t} \\ \end{aligned}
\begin{aligned} \therefore \quad S&=\int_{0}^{2π} \frac{1}{2}\left|1+2\cos{t}\right| \; dt \\ &=\int_{0}^{π} \abs{2\cos{t}+1} \; dt\\ &=\int_{0}^{\frac{2}{3}π} \left(2\cos{t}+1\right) \; dt-\int_{\frac{2}{3}π}^{π} \left(2\cos{t}+1\right) \; dt \\ &=\left[t+2\sin{t}\right]_{0}^{\frac{2}{3}π}-\left[t+2\sin{t}\right]_{\frac{2}{3}π}^{π}\\ &=2\left(\frac{2}{3}π+\sqrt{3}\right)-π \\ &=\frac{π}{3}+2\sqrt{3} \end{aligned}
これは円外の部分の面積の$2$倍分足している状態ですね。
$\displaystyle S=π+2\cdot\left\{2\cdot\left(\frac{1}{2}\cdot\sqrt{3}\cdot1\right)-\frac{1}{2}\cdot1^2\cdot\frac{2}{3}π\right\}=\frac{π}{3}+2\sqrt{3}$.

$ $
$ $
$ $

斜円錐の側面積に挑戦

$\text{D}$の頂点を原点$\text{O}$、底面の円周上の点$\text{P}$ として考える。
$\text{D}$ の底面が平面$z=-h$ 上にあり、底面の円の中心は$\left(d,0,-h\right)$

$\begin{cases} x(t)=d+r\cos{t} \\ y(t)=r\sin{t} \\ z(t)=-h \end{cases} \quad \left(-π\leq t \leq π\right)$

とすると、

$\begin{cases} x'(t)=-r\sin{t} \\ y'(t)=r\cos{t} \\ z'(t)=0 \end{cases} \quad \left(-π\leq t \leq π\right)$

これを用いて
\begin{aligned} \left(x'y-y'x\right)^2 &= \left\{\left(-r\sin{t}\right)\cdot r\sin{t}-r\cos{t}\cdot\left(d+r\cos{t}\right)\right\}^2 \\ &= r^2\left(r+d\cos{t}\right)^2 \\ \\ \left(y'z-z'y\right)^2 &= \left\{r\cos{t}\cdot\left(-h\right) - 0\cdot r\sin{t}\right\}^2\\ &=r^2h^2\cos^2{t} \\ \\ \left(z'x-x'z\right)^2&=\left\{0\cdot \left(d+r\cos{t}\right) -\left(-r\sin{t}\right)\cdot \left(-h\right)\right\}^2\\ &=r^2h^2\sin^2{t} \end{aligned}

$ $

\begin{aligned} \therefore\quad & \left(x'y-y'x\right)^2+\left(y'z-z'y\right)^2+\left(z'x-x'z\right)^2 \\ =& r^2\left(r+d\cos{t}\right)^2+r^2h^2\cos^2{t}+ r^2h^2\sin^2{t}\\ =& r^2\left\{\left(r+d\cos{t}\right)^2+h^2\right\} \end{aligned}

$ $

\begin{aligned} S&=\frac{1}{2}r\int_{-π}^{π} \sqrt{\left(r+d\cos{t}\right)^2+h^2} \; dt \\ \\ &=r\int_{0}^{π} \sqrt{\left(r+d\cos{t}\right)^2+h^2} \; dt \end{aligned}
この形は第二種完全楕円積分と呼ばれる形に帰着できるようです。(ChatGPT先生より)
とりあえず積分で表すまではできたので、ここからは他の誰かにやってもらうとしましょう。合っているんでしょうかね。

あとがき

「グリーンの定理」でWikipediaで調べると、「グリーンの定理(2次元)」というが出てきます。 グリーンの定理 /Wikipedia
その説明を見てみたんですが...なにこれ。
「グリーンの定理(2次元)」の要項

また、その下に「グリーンの定理(3次元)」もあり、
「グリーンの定理(3次元)」
またもやなにこれ。
ここら辺は大学で勉強しないといけなさそうです。
途中で「ストークスの定理」というものが出てきたのですが、関係があったりするのかしら。ちょっと気になる。

更新欄

2025.11/2. 13:10 投稿