orthotransversal のなす角について
はじめに
今回の記事では, 以前 Xに投稿 した, orthotransversal のなす角についての問題の証明を行う. orthotransversal とは, 以下のような直線のことを指す.
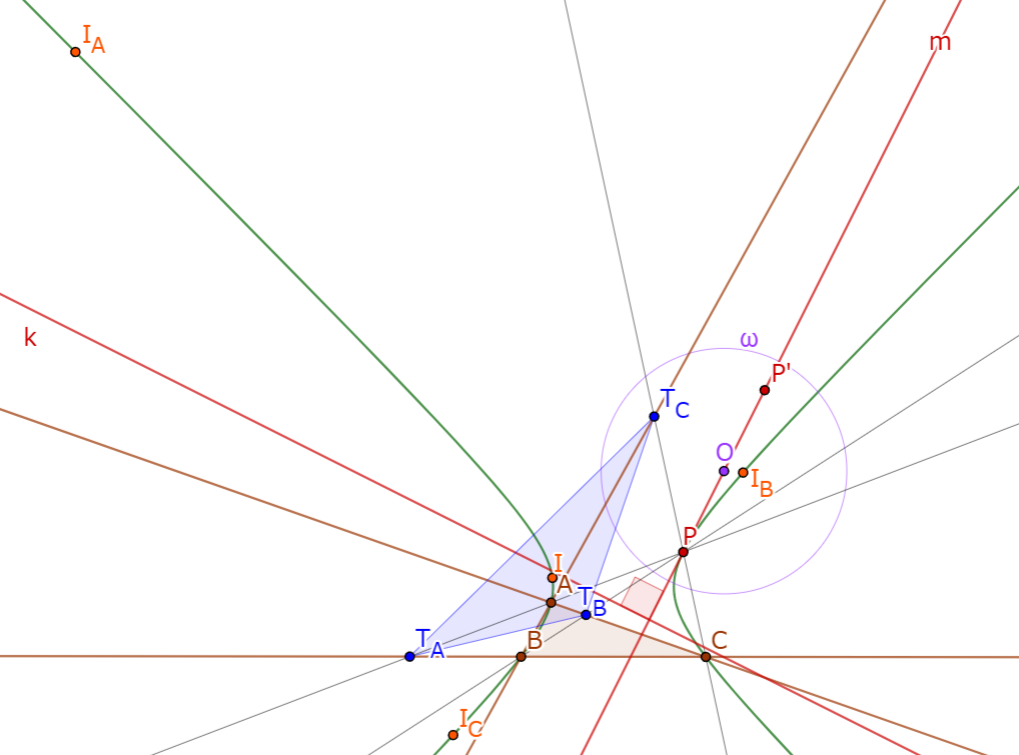
三角形$ABC$と点$P$がある. $P$を通り$PA$に垂直な直線と$BC$の交点を$D$とする. 同様にして, $P$を通り$PB$に垂直な直線と$CA$の交点を$E$, $P$を通り$PC$に垂直な直線と$AB$の交点を$F$とする. このとき, 三点$D, E, F$は一直線上にあり, またこの直線を(点$P$の三角形$ABC$における) orthotransversal と呼ぶ.
三角形$ABC$の垂心を$H$とする. $A, B, C$から対辺におろした垂線の足をそれぞれ$A_1, B_1, C_1$とする. $\angle APD = \angle AA_1D = 90°$より四点$A, P, D, A_1$は同一円周上にある. この円を$\omega_A$とする. 同様に, 四点$B, P, E, B_1$を通る円を$\omega_B$, 四点$C, P, F, C_1$を通る円を$\omega_C$とする.
$Pow_{\omega_A}(H) = Pow_{\omega_B}(H) = Pow_{\omega_C}(H) = AH \times HA_1,$
また明らかに
$Pow_{\omega_A}(P) = Pow_{\omega_B}(P) = Pow_{\omega_C}(P) = 0.$
よって三円$\omega_A, \omega_B, \omega_C$は coaxial である. するとそれら三円の中心, すなわち線分$AD, BE, CF$それぞれの中点は一直線上にあり, Newton-Gauss line の主張より三点$D, E, F$は一直線上にあることが示された.
本編
さて, 本題に入る. 今回の記事の目標は次の問題を示すことである.
中心$F$で三角形$ABC$の各点を通る直角双曲線$\mathcal{H}$と, それ上の点$P, Q$がある. 点$P, Q$それぞれの orthotransversal がなす角は, $\angle PFQ$に等しい.

まずは, いくつかの補題を示す.
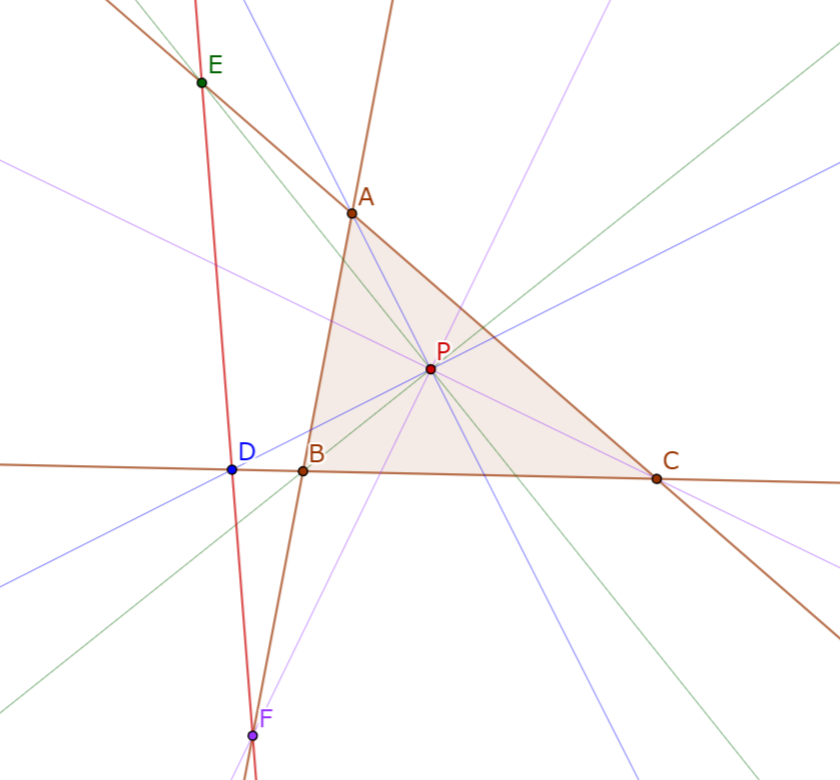
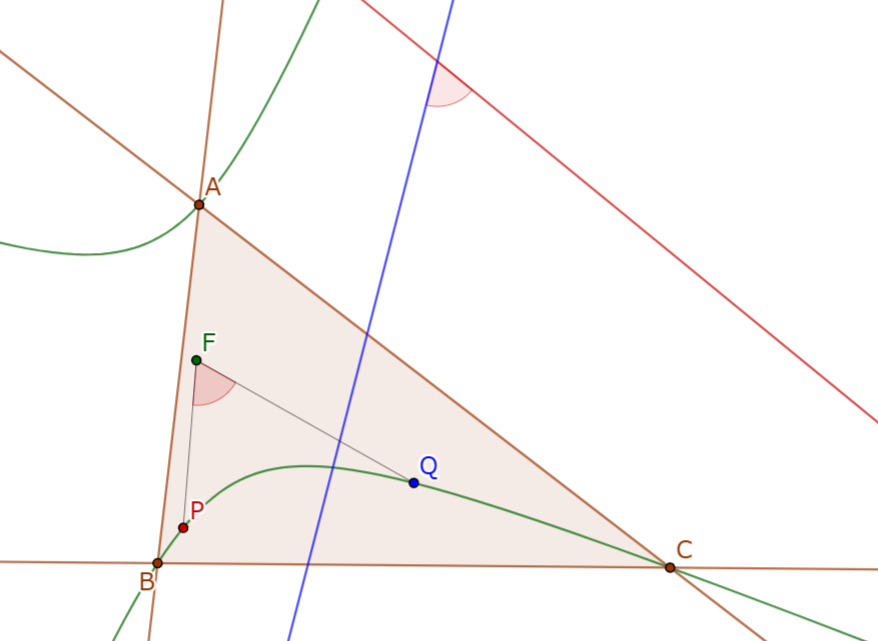
三角形$ABC$と点$P$がある. 点$A, B, C$から対辺へおろした垂線の足をそれぞれ$D, E, F$とする. 三点$A, B, C$を通る直角双曲線を$\mathcal{H}$とする. $P$の三角形$DEF$における等角共役を$Q$とする. このとき, $P$の$\mathcal{H}$における極線は$Q$を通る.
三角形$ABC$の垂心を$H$とする. $PQ$と$\mathcal{H}$の交点を$W_1, W_2$とする. $PQ$と$BC, AD, CA, BE, AB, CF$との交点をそれぞれ$X_1, X_2, Y_1, Y_2, Z_1, Z_2$とする. $PQ$を直径とする直線$PQ$上の反転$\Psi$を考える.
簡単な角度計算により$AD$は$\angle EDF$の二等分線であることがわかるので, $PD$と$QD$は$AD$に対して対称である. これと$\angle X_1DX_2 = 90°$をあわせて, $\Psi(X_1) = X_2$である. 同様にして, $\Psi(Y_1) = Y_2, \Psi(Z_1) = Z$である. 有名事実として$\mathcal{H}$は$H$を通るので, Desargues involution theorem より$\Psi(W_1) = W_2$であり, すなわち$P$の$\mathcal{H}$における極線は$Q$を通る.
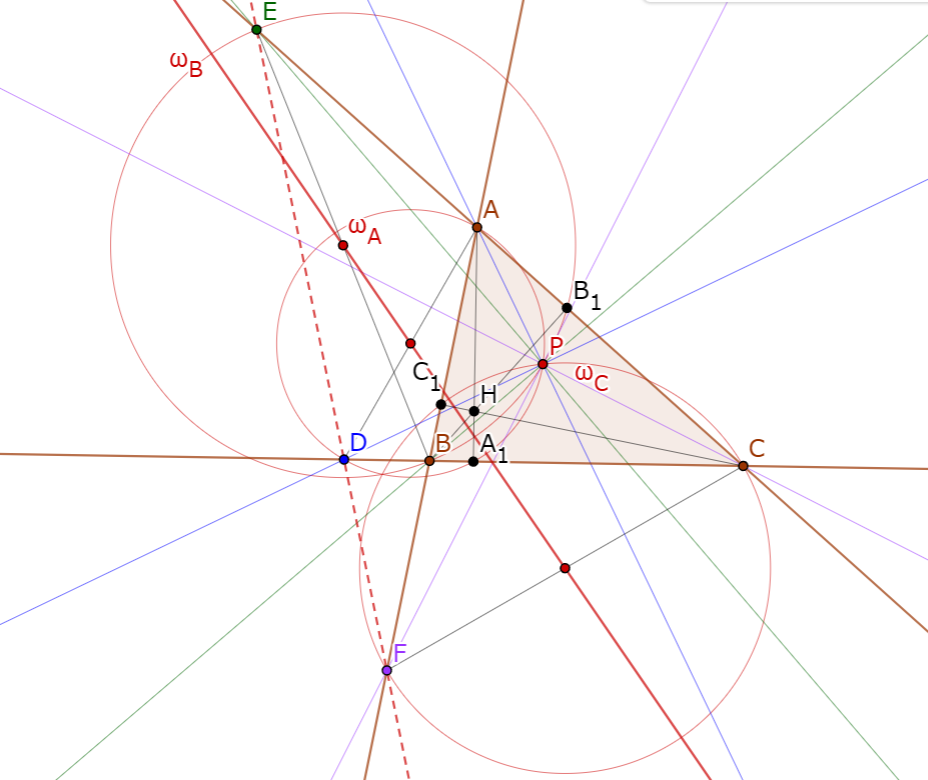
三角形$ABC$がある. 三点$A, B, C$を通る直角双曲線を$\mathcal{H}$とし, $\mathcal{H}$上に点$P$をとる. $AP, BP, CP$と対辺との交点をそれぞれ$D, E, F$とする. このとき, 三角形$DEF$の内心と傍心は$\mathcal{H}$上にある.
$\angle EDF$の内角の二等分線と$\mathcal{H}$との交点を$I_1, I_2$, $EF$との交点を$K$とする. $EI_1$と$\mathcal{H}$の交点を$I_3(\neq I_1)$, $FI_1$と$\mathcal{H}$の交点を$I_4(\neq I_1)$, $I_3I_4$と$EF$の交点を$L$とする. 適切な射影変換により, 三点$I_3, I_4, D$, $I_4, I_2, E$, $I_2, I_3, F$の共線がわかる. すると$(E, F; K, L) = (I_4, I_3; D, L) = -1$なので, $\angle EDK = \angle FDK$とあわせて$DK \perp I_3I_4$を得る. すると, $\mathcal{H}$が直角双曲線であることから四点$I_1, I_2, I_3, I_4$が垂心系をなすことがわかり, 示された.

次の補題はよく知られているものである.
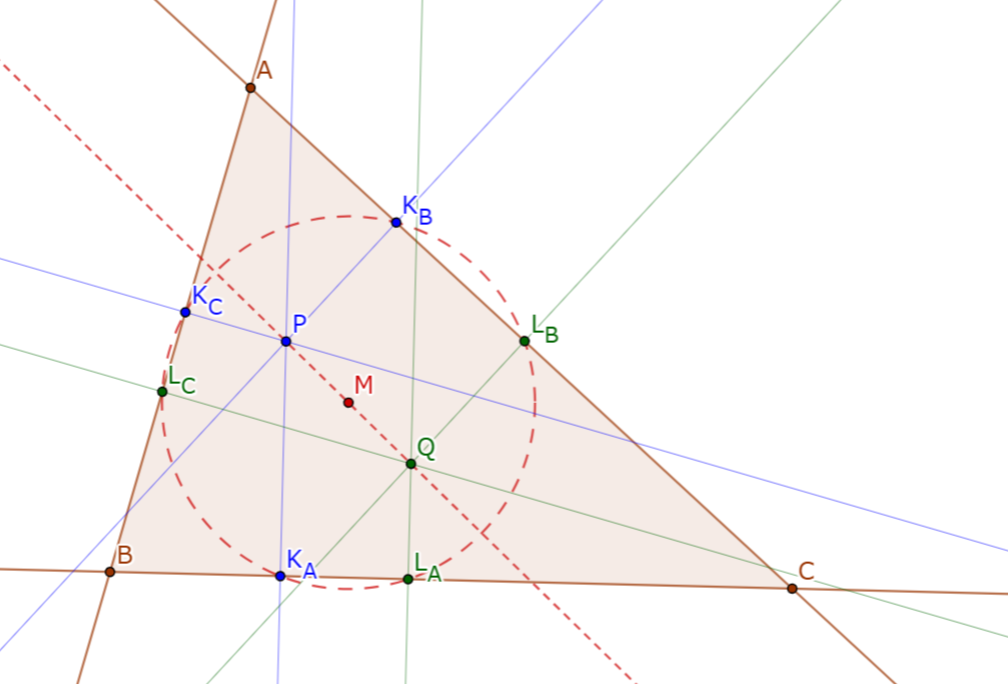
三角形$ABC$と点$P$がある. $P$の等角共役を$Q$とする. $P$と$Q$の垂足円は一致し, その中心は$PQ$の中点である.
$P$から$BC, CA, AB$におろした垂線の足を$K_A, K_B, K_C$とする. $Q$から$BC, CA, AB$におろした垂線の足を$L_A, L_B, L_C$とする. $PQ$の中点を$M$とする. 簡単な角度計算により四点$K_A, K_B, L_A, L_B$が同一円周上にあることがわかる. また, $K_AL_A, K_BL_B$それぞれの垂直二等分線は$M$を通ることから, 円$K_AK_BL_AL_B$の中心は$M$であることがわかる.
同様にして, 四点$K_BK_CL_BL_C$は同一円周上にあり, その中心は$M$であることがわかる. よって, 中心$M$で六点$K_AK_BK_CL_AL_BL_C$を通る円が存在する.
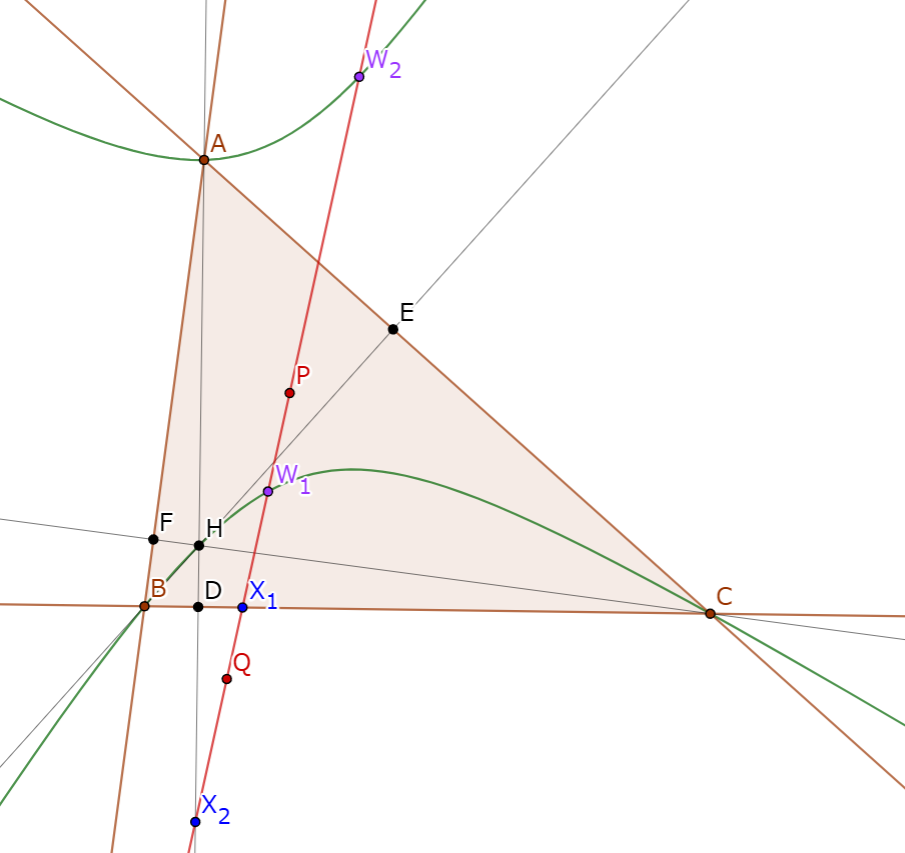
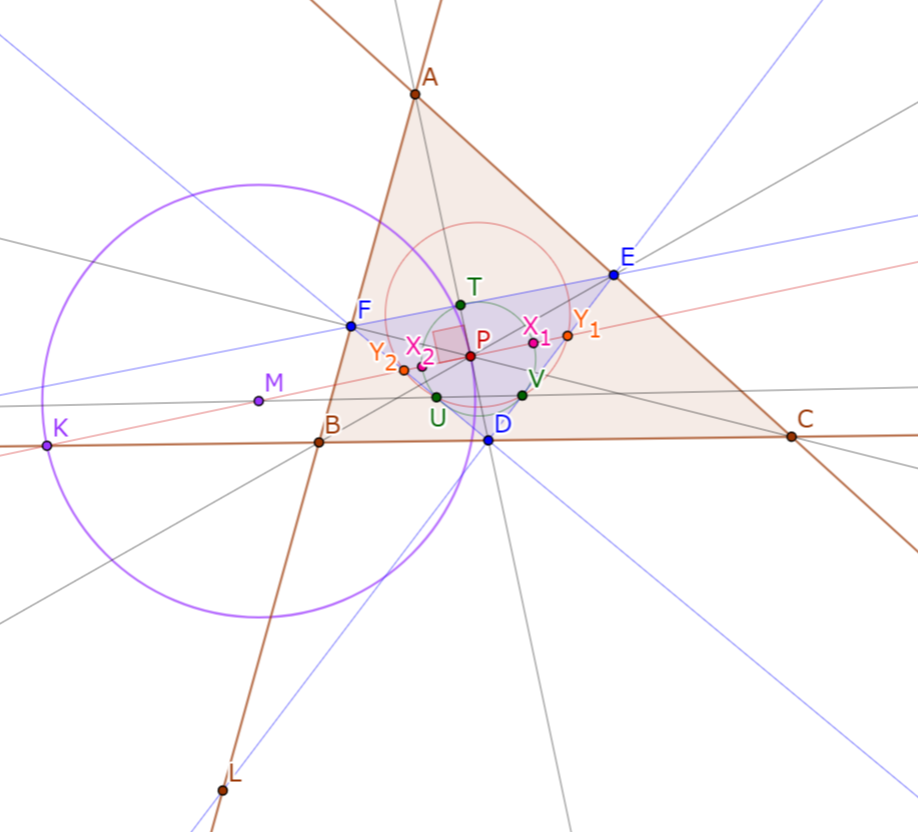
三角形$ABC$と点$P$がある. $AP, BP, CP$と対辺の交点をそれぞれ$D, E, F$とし, $P$の三角形$DEF$における垂足円を$\omega$とする. $P$の三角形$ABC$における orthotransversal を$l$としたとき, $P$の$\omega$における極線は$l$に一致する.
$P$から$EF, FD, DE$におろした垂線の足をそれぞれ$T, U, V$とする. $P$を通り$AP$に垂直な直線と$\omega$の交点を$X_1, X_2$とする. $P$を通り$AP$に垂直な直線と$BC, DE, DF, UV$との交点をそれぞれ$K, Y_1, Y_2, M$とする. $AB$と$DE$の交点を$L$とする. 対称性より, $l$が$K$を通ることを示せば十分である. 簡単な角度計算により四点$U, V, Y_1, Y_2$の共円や, 三点$P, U, V$を通る円が$PK$に接することがわかる. よって
$MP^2 = MU \times MV = MX_1 \times MX_2 = MY_1 \times MY_2$
, すなわち$M$中心半径$MP$の円の反転$\Psi$で$X_1$と$X_2$, $Y_1$と$Y_2$は互いに移りあう. また,
$(K, P; Y_1, Y_2) = (B, A; L, F) = -1$
なので$KP$を直径とする円の反転$\Psi'$で$Y_1$と$Y_2$は互いに移りあう. 以上の議論をあわせて$\Psi = \Psi'$を得る. すると$(K, P; X_1, X_2) = -1$であり, $l$は$K$を通ることが示された.
補題の証明は以上である. それでは, 主問題の証明を行う.
問題 1 の再掲
中心$F$で三角形$ABC$の各点を通る直角双曲線$\mathcal{H}$と, それ上の点$P, Q$がある. 点$P, Q$それぞれの orthotransversal がなす角は, $\angle PFQ$に等しい.
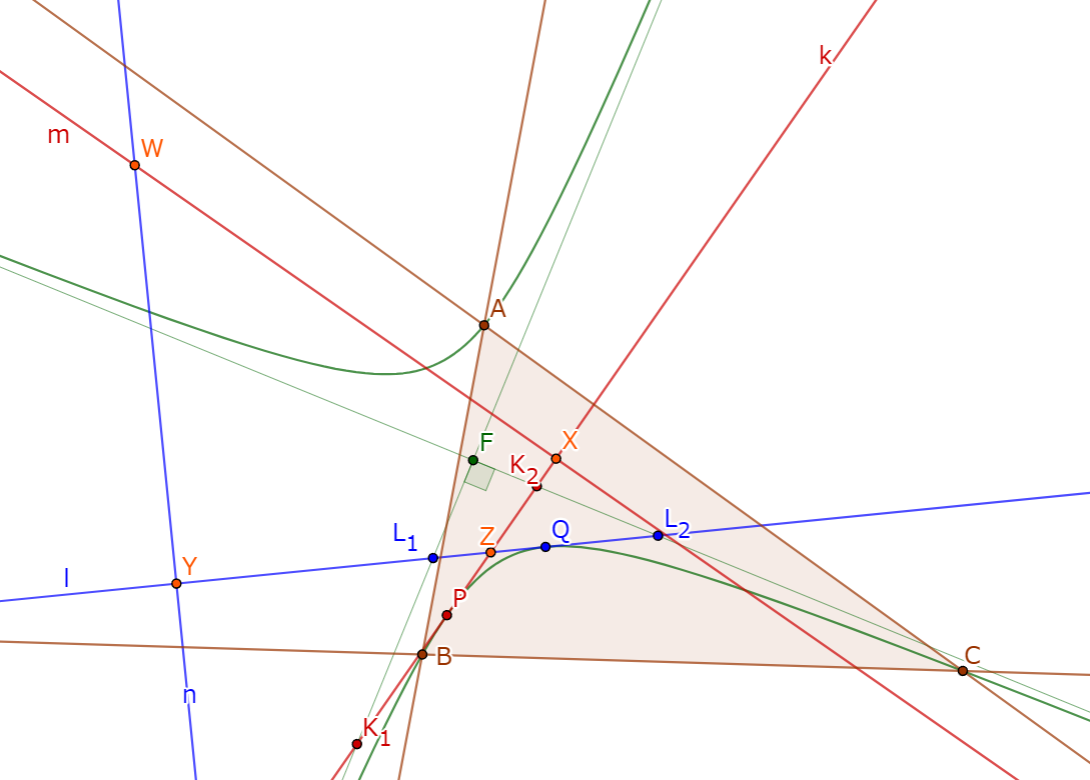
$P, Q$から$\mathcal{H}$にひいた接線をそれぞれ$k, l$とする. $P, Q$の orthotransversal をそれぞれ$m, n$とする. $m$と$n$の交点を$W$, $k$と$m$の交点を$X$, $l$と$n$の交点を$Y$, $k$と$l$の交点を$Z$とする. $\mathcal{H}$の漸近線と$k$の交点を$K_1, K_2$, $\mathcal{H}$の漸近線と$l$の交点を$L_1, L_2$とする. 有名事実として$P$は$K_1K_2$の中点であるから, $\angle K_1FK_2 = 90°$とあわせて$\angle FPZ = 2 \times \angle PFK_1$である. 同様にして, $\angle FQZ = 2 \times QFL_2$である. すると,
$\angle PZQ = \angle FPZ + \angle FQZ + \angle PFQ = 2(\angle PFK_1 + \angle QFL_2) + \angle PFQ = 180° - \angle PFQ$.
よって, $\angle XWY = \angle PFY = 180° - \angle PZQ$を示せばよい. 以下, より強く$k$と$m$, $l$と$n$がそれぞれ直交することを示す.
$AP, BP, CP$と対辺との交点をそれぞれ$T_A, T_B, T_C$とする. $P$の三角形$T_AT_BT_C$における垂足円を$\omega$, $P$の三角形$T_AT_BT_C$における等角共役を$P'$とおく. $\omega$の中心を$O$とおく. 三角形$T_AT_BT_C$の内心と傍心を$I, I_A, I_B, I_C$とおく. 補題 3 より, 四点$I, I_A, I_B, I_C$は$\mathcal{H}$上にある. すると, 三角形$I_AI_BI_C$と点$P$に補題 2 を使うことにより$PP'$は$\mathcal{H}$に接することがわかる. よって, $PP'$と$m$は一致する. ここで, 補題 4より三点$P, O, P'$は一直線上にあり, 補題 5 よりこの直線は$k$に直交する. よって$m$と$k$は直交し, これは$n$と$l$についても同様である. 以上より示された.