コラッツ予想の証明（エイプリルフールではないですよ）

第1章 初めに

任意の正の整数$n$に対して、以下の操作を考える。
　・${n}$が奇数の場合、${n}$を3倍して1を足す
　・${n}$が偶数の場合、${n}$を2で割れなくなるまで割る
このとき、「どんな初期値から始めても、有限回の操作のうちに必ず1に到達する」という主張が「コラッツ予想」である。

本稿は「コラッツ予想」が成立することを確率的なアプローチを使って証明する。なお、本稿では、上記操作を行って得られた数列を「コラッツ数列」、その数列を得ることを「コラッツ展開」と呼ぶことにする。また、本質的に奇数部分のみを考えれば良いので、特に断りのない限り、コラッツ数列は以下のように偶数部分を省いた数列のみで記述されるものとする。
　①初期値29： 29→11→17→13→5→1
　②初期値39： 39→59→89→67→101→19→29→11→17→13→5→1
　③初期値57： 57→43→65→49→37→7→11→17→13→5→1

第2章 本稿の要旨①（コラッツ展開を表す漸化式）

本稿の結論を最初に述べると、「ある初期値$b_0$から始まるコラッツ数列は以下の漸化式を使って書き表すことができる」ということになる。

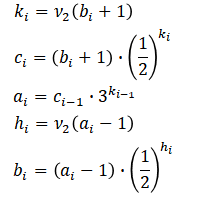
ここで、関数$ν_p(n)$は「整数$n$を割り切れるような$p$-冪のうちの最大の冪指数」を表す。参考までに、具体的な例をいくつか挙げておく。

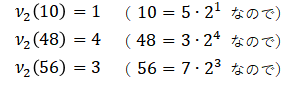
この漸化式がなぜコラッツ数列を表すかについては後ほど詳しく述べるが、ここでは幾つかの初期値から漸化式を使って得られた数列${\{}b_i\}$とコラッツ数列を比べて、両社が合致していることだけ確認する。

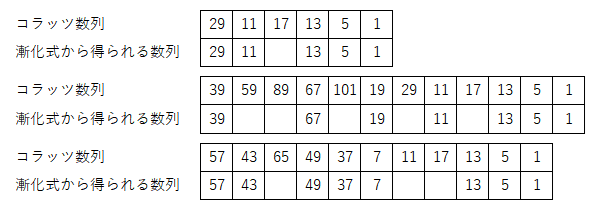
なお、漸化式から得らる数列$\{b_i\}$は途中に空白が入っており、コラッツ展開とは完全には合致していない。この点についても後ほど語るので、ここではあえて気にせず先に議論を進めたい。

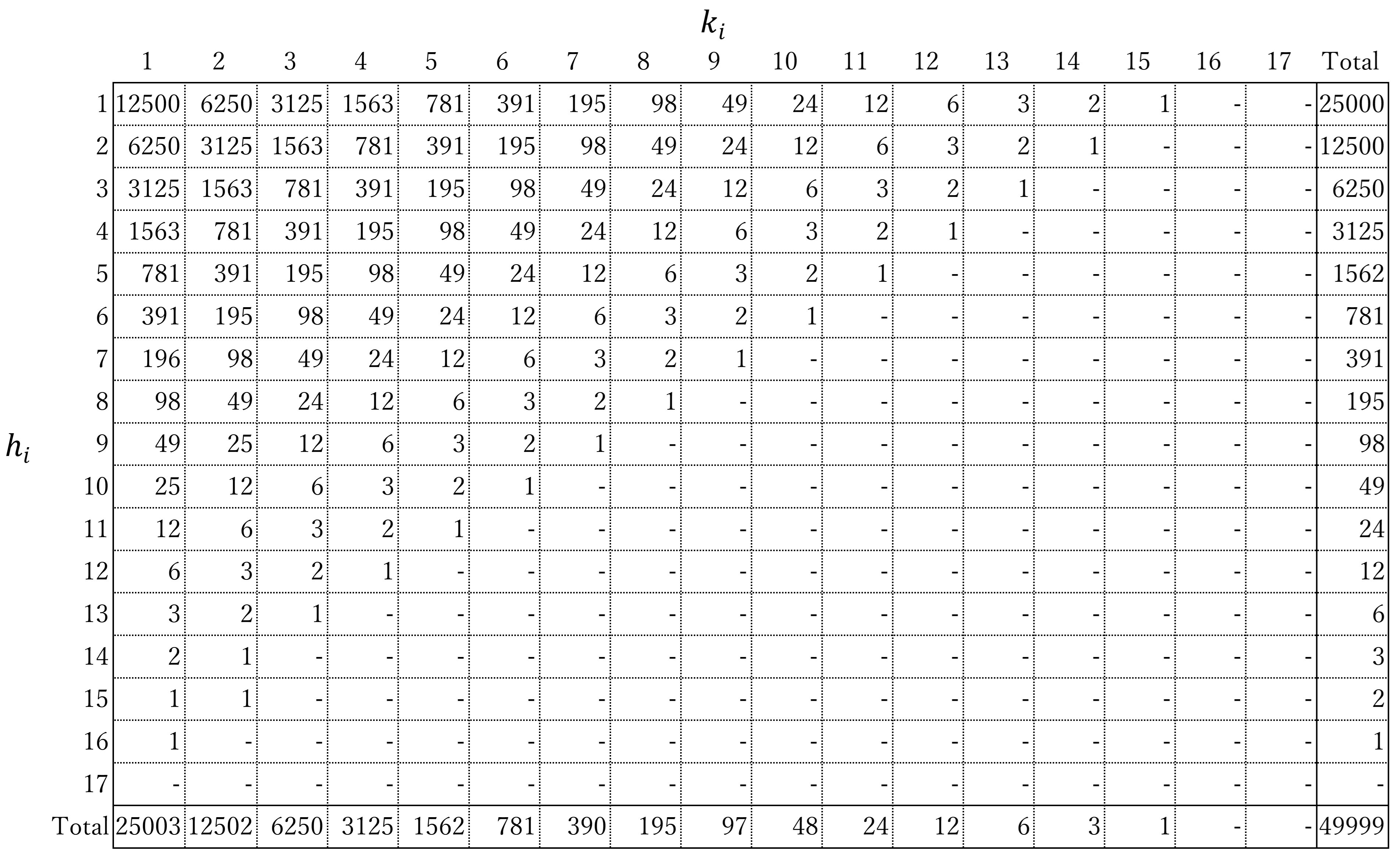
それから、各初期値に対する漸化式の各変数$(a_i,h_i,b_i,k_i,c_i)$の推移は以下のようになる。検証する際の参照としてほしい。

第3章 本稿の要旨②（コラッツ予想の証明）

この数列$\{b_i\}$を使うことで、コラッツ予想を証明できる。

3-1.コラッツ数列の上限

まず、変数$b_i$に関して他の変数$(a_i,h_i,k_i,c_i)$を使って計算すると、以下のようになる。

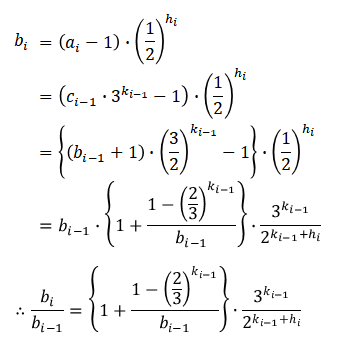
したがって、初期値$b_0$から計算される数列$\{b_i\}$の$m$ステップ目の変数$b_m$を計算すると、以下のようになる。

なお、ここでは以下で定義される新たな変数$(H_m,K_m)$を使っている。

 
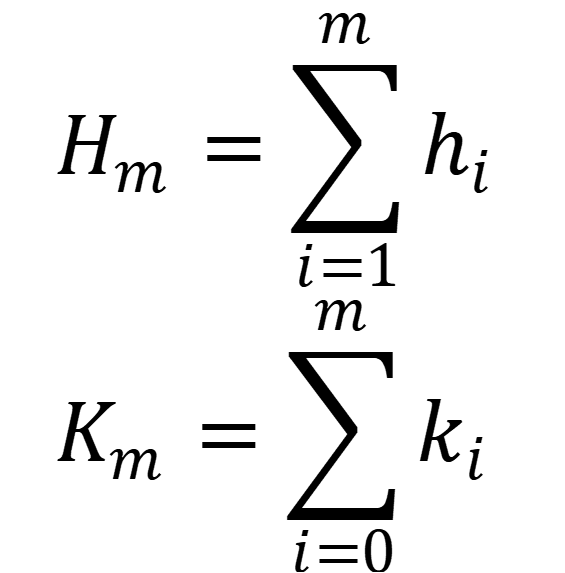
ここで、任意の$i(i≥0)$に対して$0< k_i$かつ$3≤b_i$なので、以下が成り立つ。

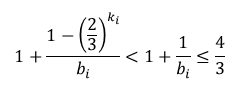
したがって、変数$b_m$は以下のような上限を持つことが分かる。

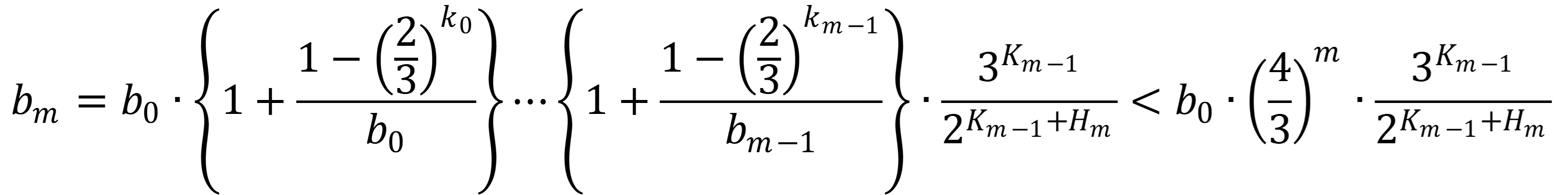
3-2.HK分布

さて、ここで変数$(h_i,k_i )$の振る舞いを考えてみる。$(h_i,k_i )$の定義は以下なので、どちらも変数$a_i$から計算することができる。

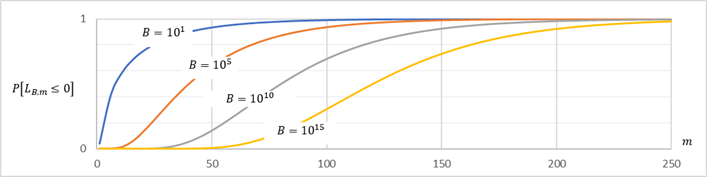
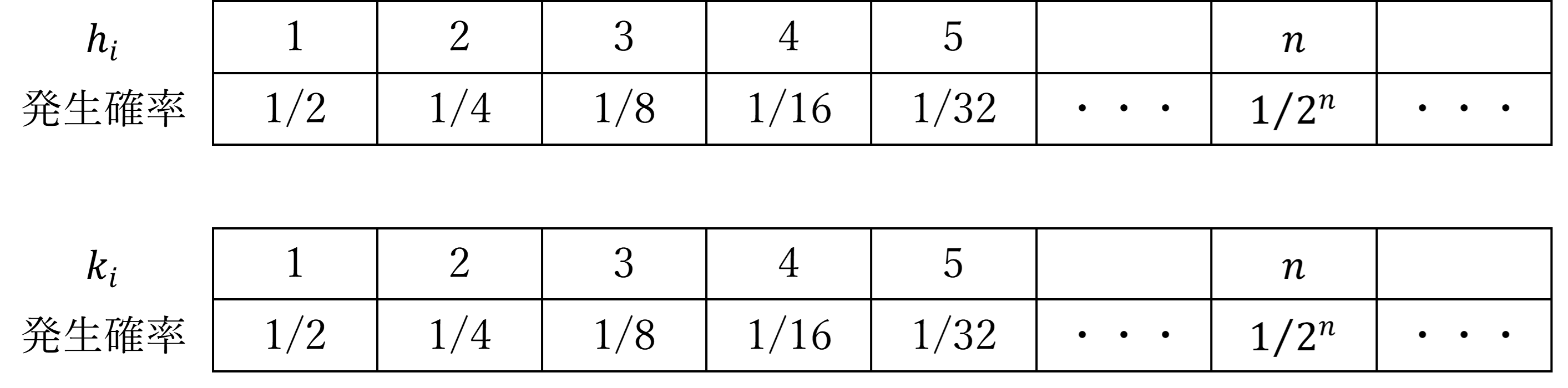
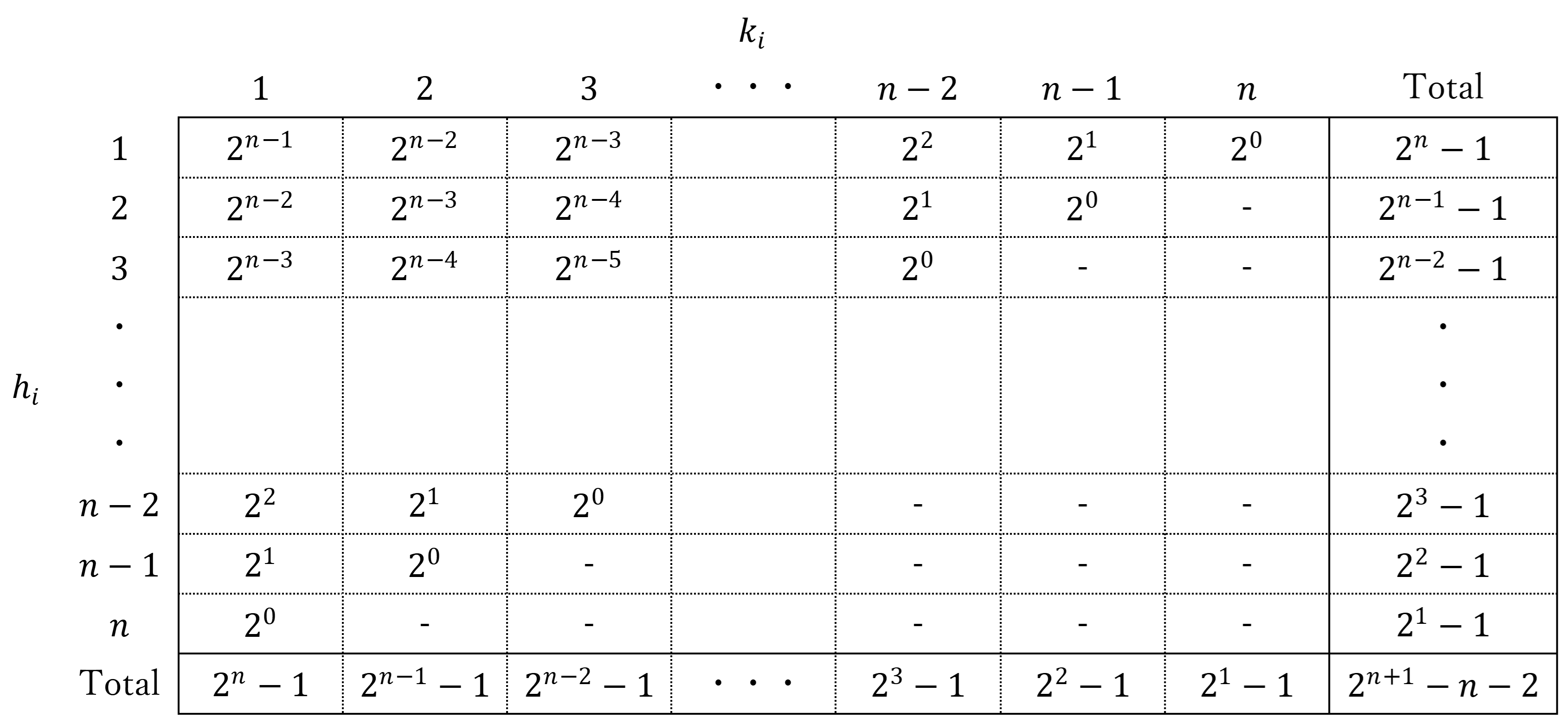
詳しくは後述するが、上記から変数$(h_i,k_i )$はそれぞれ独立した確率変数のように扱うことができ、その値の発生確率はいずれも以下のようになる。本稿では、この分布を「HK分布」と呼ぶこととする。

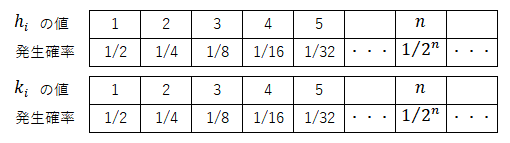
このHK分布を前提とすると、変数$(h_i,k_i)$の平均$E$と分散$V$は以下のように計算できる。

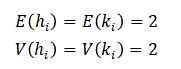
そのため、変数$(H_m,K_m)$の平均$E$と分散$V$は以下の通りとなる。

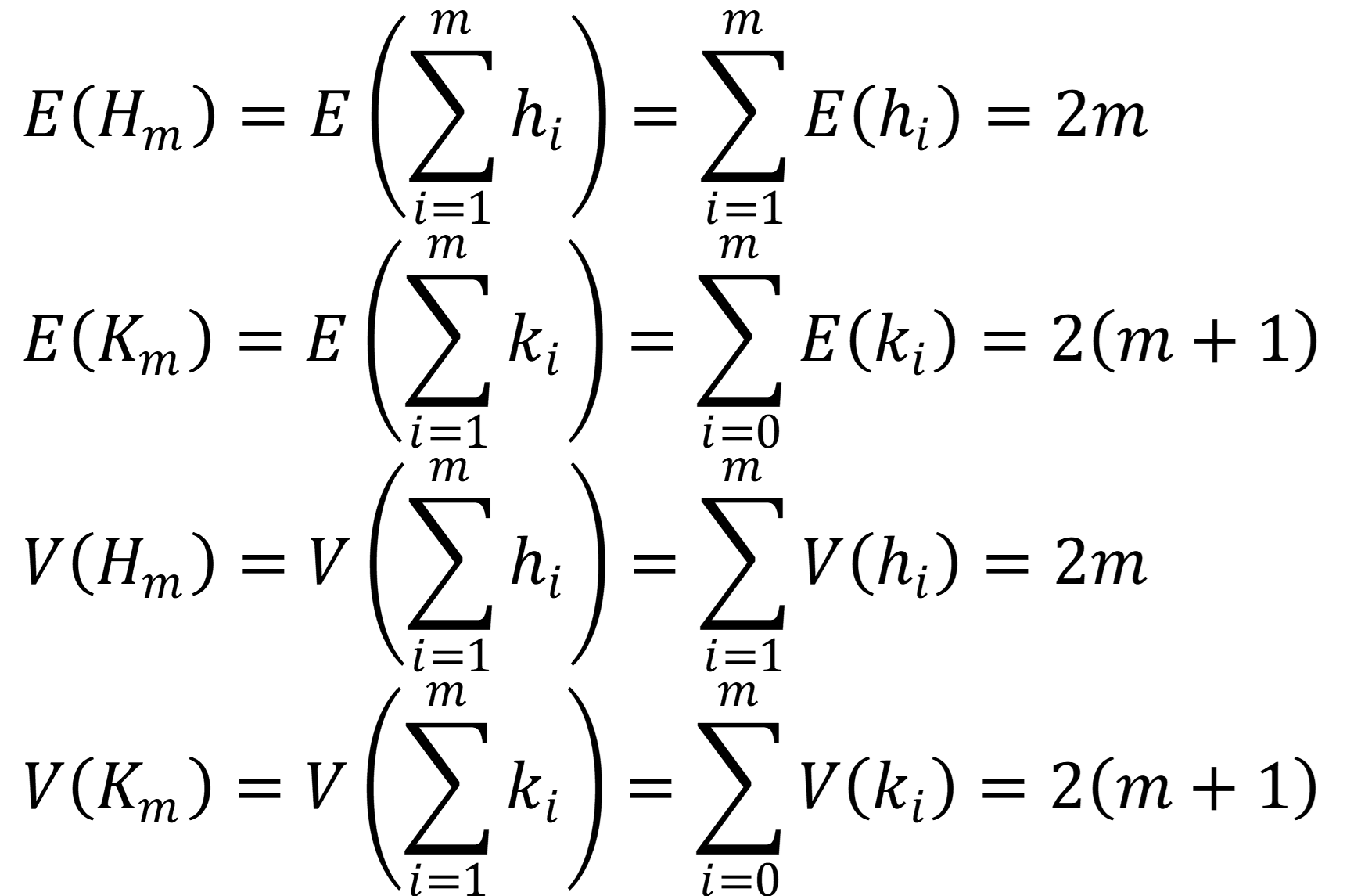
3-3.コラッツ予想の（直感的な）証明

さて、ここでコラッツ予想が成り立つことを直感的に考えてみる（精緻な証明は次節で行う）。

先ほど、変数$b_m$は以下のような上限を持つことを示した。

ここで、変数$(H_m,K_m)$の平均値を考えると、変数$b_m$の期待値は以下になる。そのため、$m$が十分に大きいとき、変数$b_m$は初期値$b_0$より十分に小さくなることが（直感的に）理解できる。

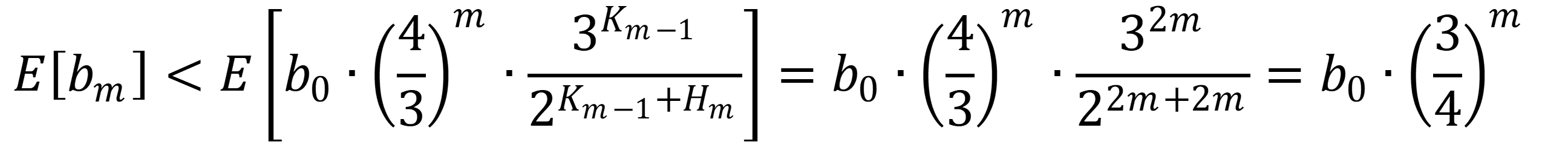
3-4.コラッツ予想の（より精緻な）証明①

前節の議論は少し乱暴なので、本節ではもう少し精緻に考えてみたい。

これまでコラッツ予想は様々な検討がなされており、一定の初期値以下であれば成り立つことが確かめられている。そこで、過去の検証でコラッツ予想が成り立つことが確認されている初期値のうち、最大の数を$b_M$と書くことにしよう。

すると、我々が証明する必要があるのは、以下の命題ということになる。

さらに先ほどの上限の議論を踏まえると、これは以下を証明すれば良いことになる。

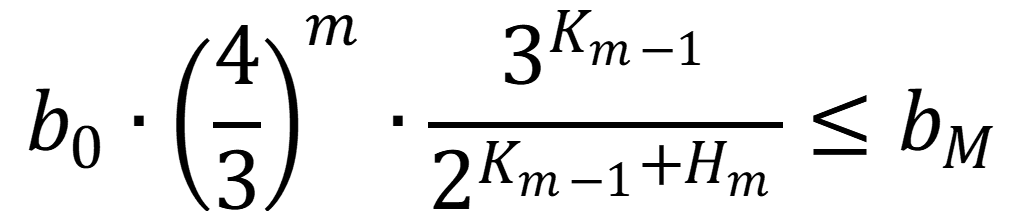
ここで、変数$B$と変数$L_{B,m}$を以下で定義する。

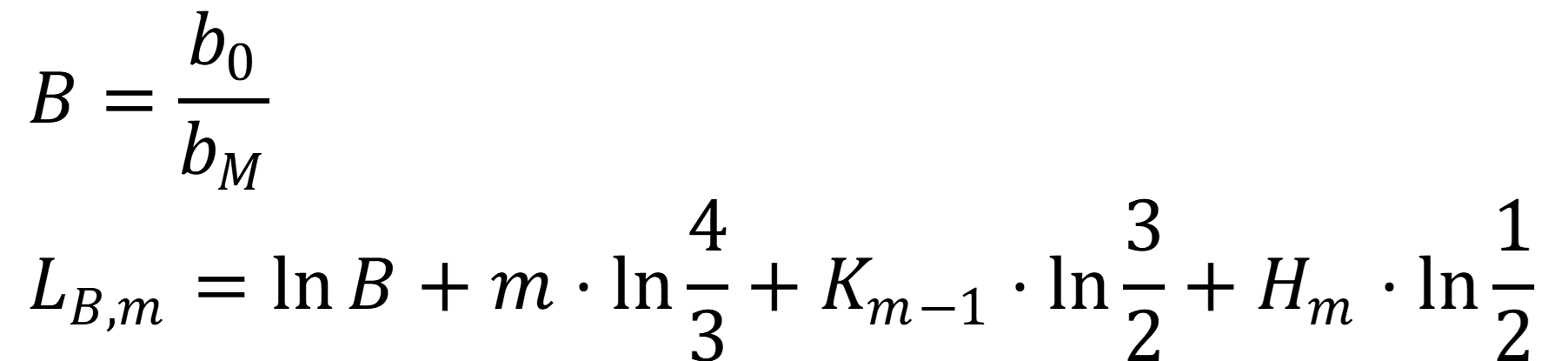
すると、証明すべきは以下の不等式になる。

本稿ではコラッツ予想を証明するために確率的なアプローチをとることにする。すなわち、上記で定義された変数$L_{B,m}$が$0$以下になる確率$P[L_{B,m} \leq 0]$に関して、以下のように「ステップ数$m$が大きくなると限りなく$1$に近づく」ことを証明する。

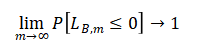
3-5.コラッツ予想の（より精緻な）証明②

さて、ここで変数$(H_m,K_m)$の定義を思い返してほしい。変数$(H_m,K_m)$は以下で定義されており、各変数$(h_i,k_i)$は独立でHK分布に従うと仮定している。

そのため、ステップ数$m$が十分に大きい場合、中心極限定理により変数$(H_m,K_m)$は正規分布に従うので、$L_{B,m}$の確率分布も以下のグラフのような正規分布を取ることになる。

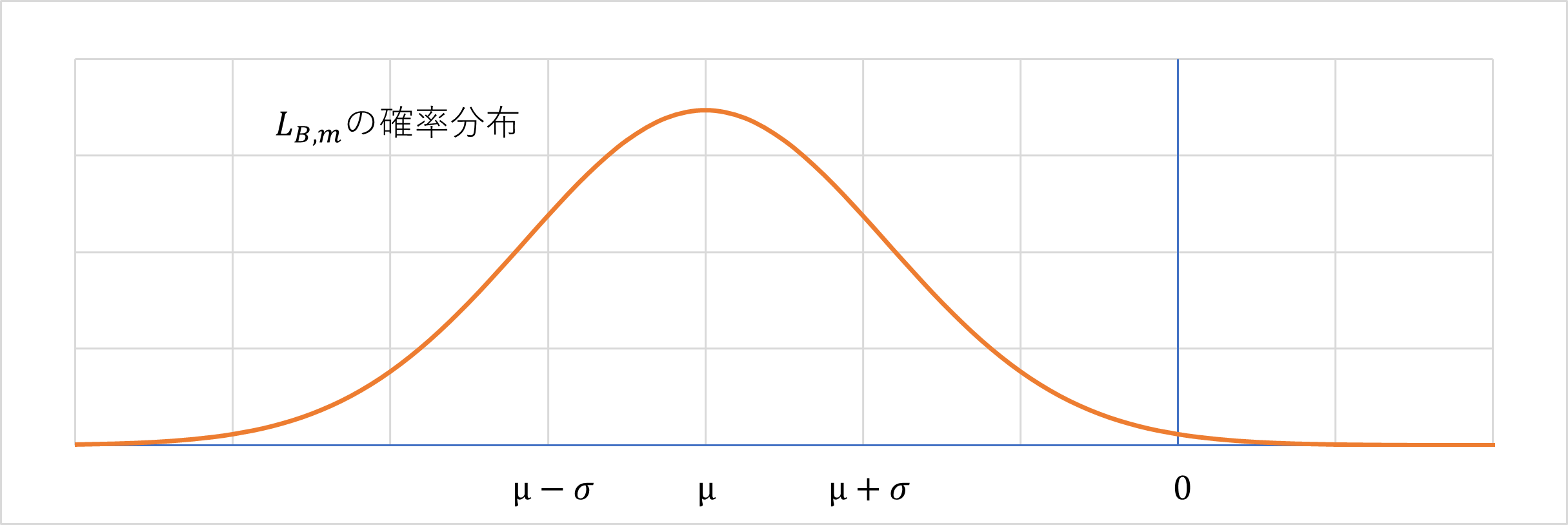
なお、この確率分布の平均値$\mu$と分散$\sigma^2$は以下で計算される。

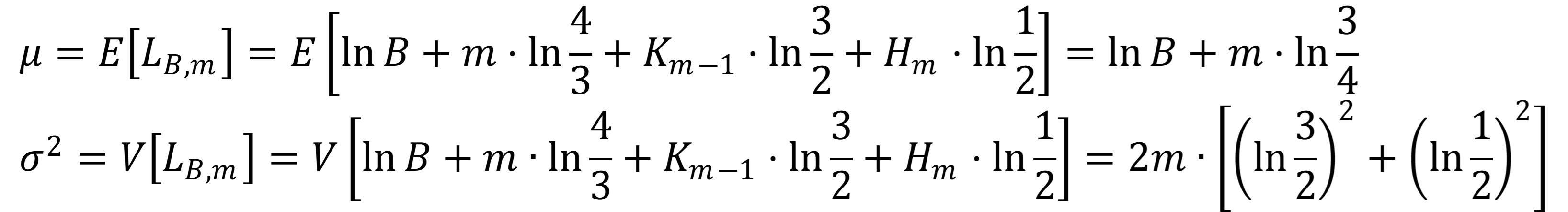
この確率分布を仮定すると、$L_{B,m} \leq 0$となる確率$P[L_{B,m} \leq 0]$は以下のようになる。

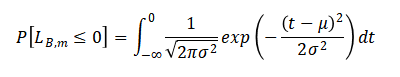
この式の右辺は正規分布の累積分布関数なので、簡単に計算できる。実際に計算すると、$P[L_{B,m} \leq 0]$のグラフは以下となり、ステップ数$m$を十分に大きくすると確率$P[L_{B,m} \leq 0]$は$1$に収束することが分かる。

したがって、コラッツ予想は$b_M$以上の初期値でも成り立つことが分かる。

第4章 コラッツ展開の視覚化（コラッツ・マップ）

前章までで、証明までの論理展開は一通り行った。本章からは、この結論に至った過程で重要と思われる、以下の2点について検証していくこととする。

この①②が分かれば、先ほどの議論で述べた通り、以下が成り立つので、コラッツ予想はどんな整数でも成り立つと言うことができる。

では、この2点を検証していこう。まず、最初に検討するのは、「①コラッツ数列を以下の漸化式を使って表すこと」である。

これを説明するためには「コラッツ・マップ」というものを理解する必要がある。これはコラッツ数列を視覚化したもので、これが分かれば上記漸化式がなぜ成り立つかも理解できると思う。図を使うので話が少し長くなるが、コツをつかめれば理解自体は容易いので少しの間ご辛抱いただきたい。

4-1.コラッツ・マップ①

まず、以下のような表を使ってコラッツ展開を視覚化することから始めたいと思う。なお、本稿ではこの表のことを「コラッツ・マップ」（または省略して単に「マップ」）と呼ぶことにする。

このコラッツ・マップの特徴は以下の通りである。

特徴①：各行の値は最上段の指数で重みづけされた数となる。

例えば、以下の数字列は「19」を表すことになる。

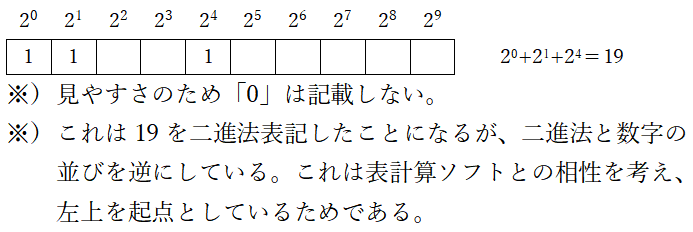
なお、この表に入る数字は特に限定しない。そのため、次の表はどちらも同じ数字を表現していることになる。

特徴②：上段にある数字列を一段下におろす場合、数字列を3倍する。

 
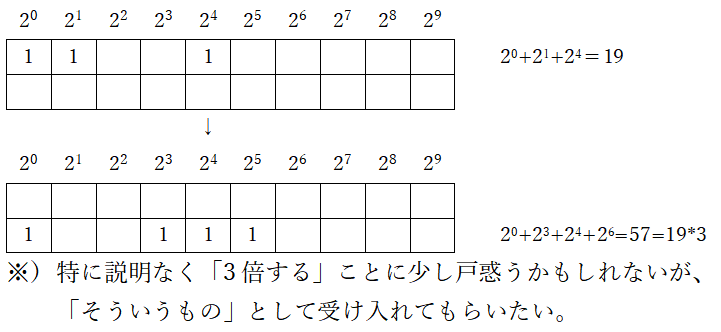
なお、これに「1を足す」操作を施して整理すると、以下のようになる。
 

特徴③：「2で割れるだけ割る」操作は、以下のように最小の桁が「1」になるように指数を振り直すことに該当する。

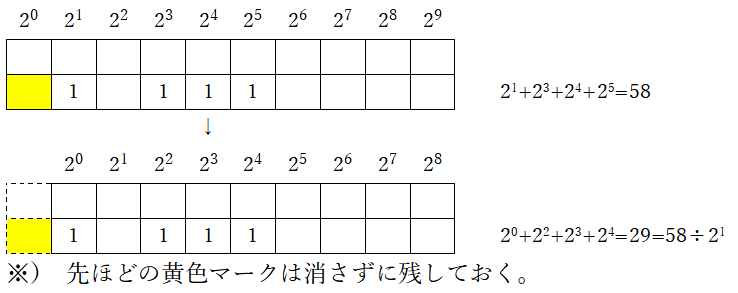
4-2.コラッツ・マップ②

これらの特徴を使うことで、コラッツ展開を視覚化することができる。ここでは「初期値17」を例にして説明する。

0）初期値17を設定する

1）3倍して１を足し、2で割り切る（1を足す場所には黄色マークを付ける）

2）同様の操作（3倍して１を足し、2で割り切る）を行う

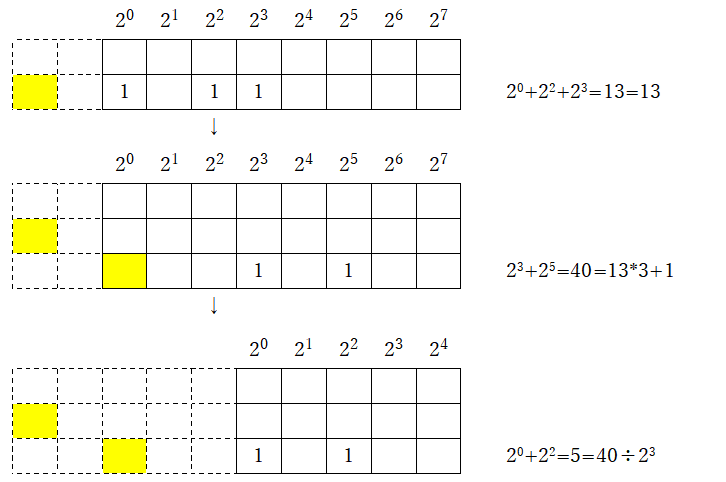
3）再び、同様の操作（3倍して１を足し、2で割り切る）を行う

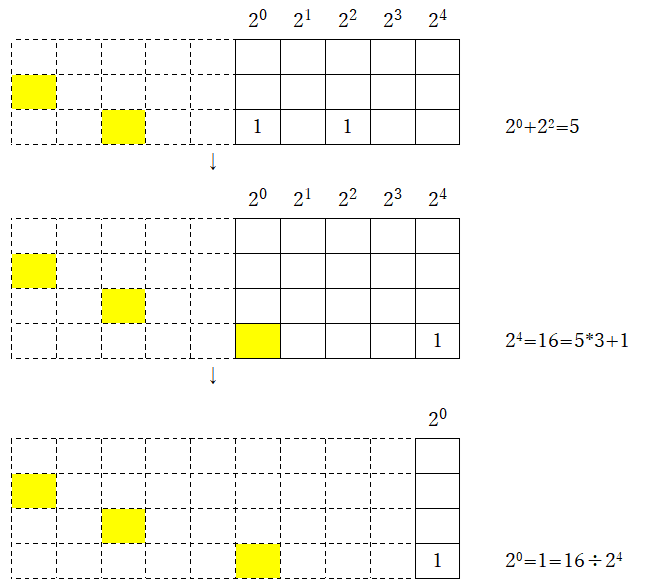
4）集計値が「1」となった時点で、操作は終了となる。

第5章 コラッツ・マップの作成方法

5-1.コラッツ・マップ

前章で導入した黄色マークに加え、本章で以下のような緑色マークとオレンジ色マークを導入し、コラッツ・マップの作成方法を説明する。

なお、これから述べることは少し回りくどく、あまり意味がないように見えるかもしれないが、その重要性については後々分かってくると思うのでお付き合い願いたい。また、見やすさを考えて、最上段の重み付けも省略する。

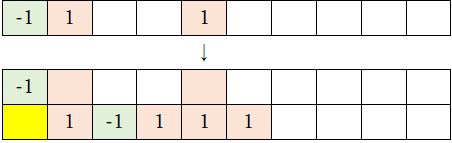
0）まず、初期値17を設定する。ただし、以下のように左端を「-1」とし、それに合わせて数字列を少し変形している。さらに、「-1」の場所には緑色、「1」の場所にはオレンジ色のマークをつける。

1-1）この「-1」の下に黄色マークを付ける。

1-2）「-1」の右側にある数字列（太枠で囲まれた部分）を下行に移動させる（下行に移動した数字列は3倍する）。なお、「-1」は元の場所に残したままにする。

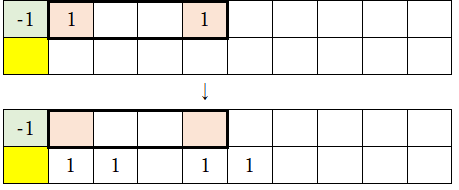
1-3）最下行の数字列を変形する。ただし、今度は左から2番目にある「1」を「-1」に置き換える（太線枠内が変形される部分）。そして、緑色とオレンジ色のマークをつける。

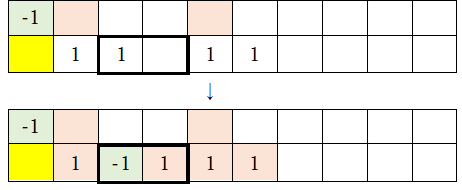
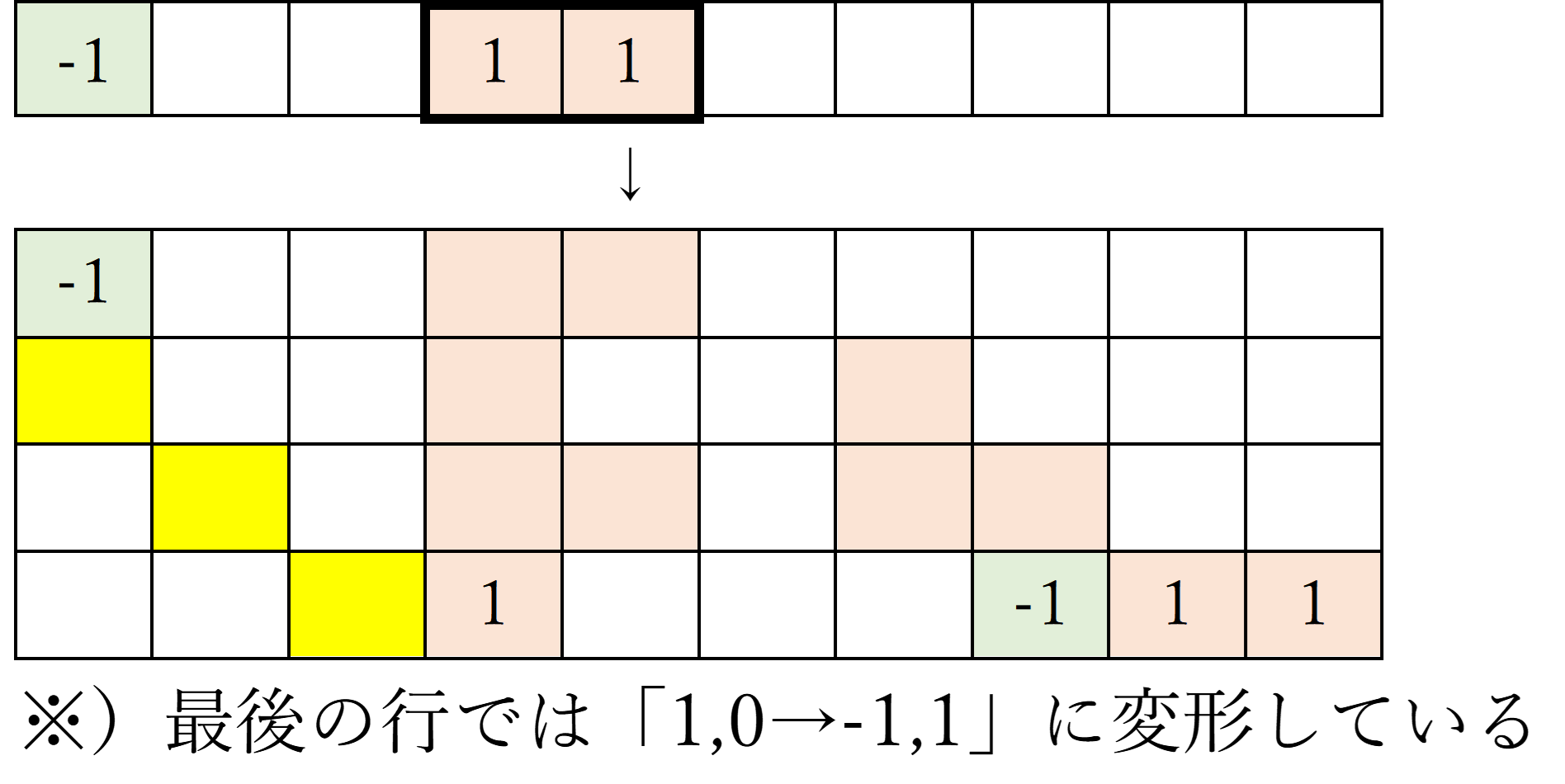
2-1）先ほどと同様に「-1」の下に黄色マークを付け、「-1」の右側にある数字列（太枠で囲まれた部分）を下行に移動させる（下行に移動した数字列は3倍する）。

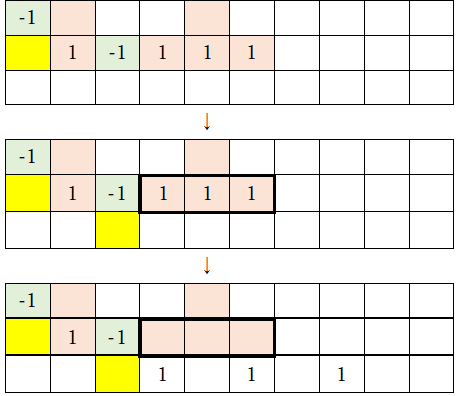
2-2）さらに、こちらも先ほどと同様に、最下行の左から2番目にある「1」を「-1」に置き換える（太線枠内が変形される部分）。そして、緑色とオレンジ色のマークをつける。

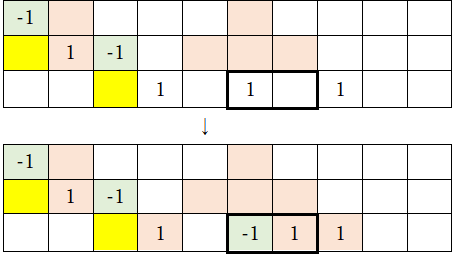
3-1）ふたたび「-1」の下に黄色マークを付け、「-1」の右側にある数字列（太枠で囲まれた部分）を下行に移動させる（下行に移動した数字列は3倍する）。

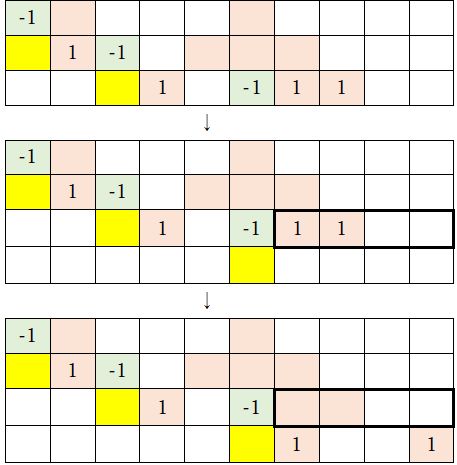
4）最下行の数字列が「1,0,…,0,1」になったところで終了となる。

このように3色のマークを導入することで、ある初期値から始まるコラッツ数列がどのような経路をたどり、最終的に1に収束したのかを視覚的に理解することができるようになる。

5-2.コラッツ・マップに関する補足説明

前節までで、コラッツ・マップの概要について説明することができた。本節では、いくつかの補足説明をする。

①「-1」と右隣の「1」との間が空いている場合

先ほどの初期値「17」の例では、以下のように「-1」のすぐ右隣に「1」があったため、「-1」の真下に黄色マークを付けるだけで済んだ。

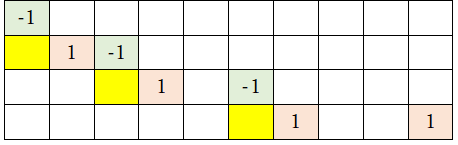
しかし、常にそうなるわけではない。たとえば初期値「23」のマップを見ると、「-1」と次の「1」との間に何マスかゼロが続く。このような場合は、以下のように黄色マークを斜め下に下す。

そして、「-1」の「-1」の右側にある数字列（太枠で囲まれた部分）を下行に移動させる。なお、「移動した数字列は3倍する」というルールは変わらないので、数列「1,1」（十進法では3）は下行に移動する毎に「1,0,0,1→1,1,0,1,1→1,0,0,0,-1,1,1」（十進法では9→27→81）と数が大きくなる。

②表中に「1」や「-1」を残す意味

上記の「コラッツ・マップの作成方法」では、表中に数字「1」と「-1」を残しているが、その意味について説明する。なお、分かりやすいように、ここの議論に関係のないマークは外しておく。

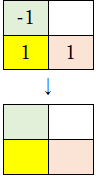
実は前節でコラッツ・マップを作成するとき、「1を加える」操作を行っていなかった。そこであらためて黄色マークに「1を加える」操作を施すとマップは以下のようになる。

ここで以下の部分に注目してほしい。この「-1」を下に移動させると下行の「1,1」と打ち消しあうため、その値はゼロになる。

つまり、以下の各太枠で囲まれた部分はいずれもゼロとなり、結果的に最後の「1」だけが残る。そのため、コラッツ数列が「1」に収束ことが直感的に確認できるのである。

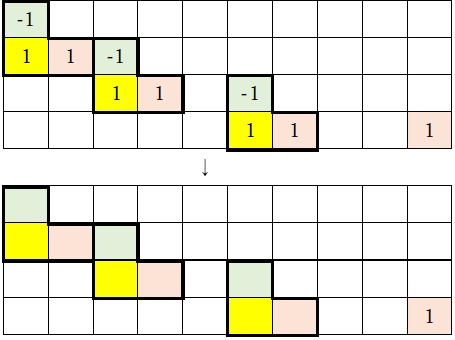
なお、以下のように黄色マークが斜めに複数置かれた場合であっても、同様に太枠で囲まれた部分は全て打ち消しあって最終的に全てゼロとなるので、同様の議論ができる。

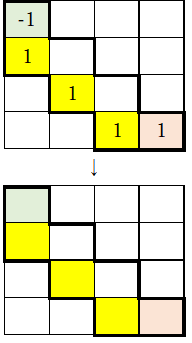
③コラッツ・マップの例

コラッツ・マップへの理解を深めるために、いくつかの初期値と対応するマップを以下に示す。なお、先ほど説明したように太枠で囲まれた部分はいずれもゼロとなるので、その部分の数字を省略している。

初期値13（13→5→1）の場合

初期値17（17→13→5→1）の場合

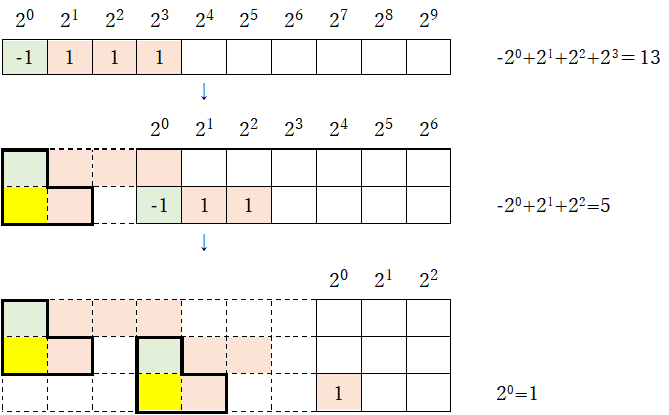
初期値23（23→35→53→5→1）の場合

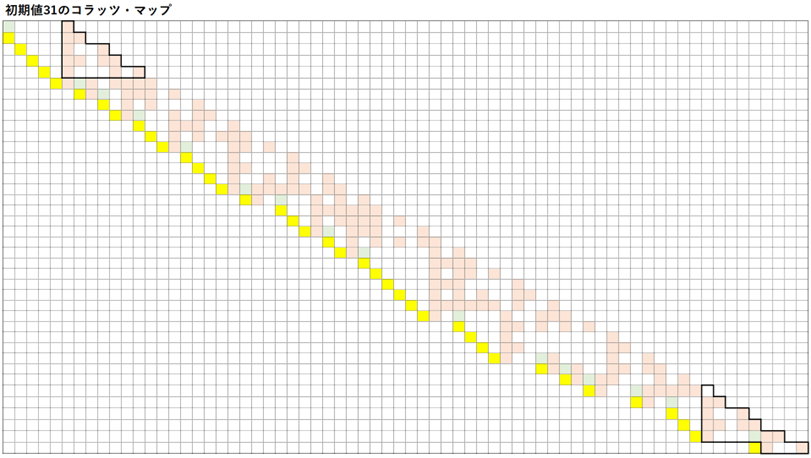
初期値31
このコラッツ数列は以下のように非常に長くなるので、マップもかなり大きくなる（初期値31のマップが大きくなる理由については、後ほど別の章で取り上げる）。
31→47→71→107→161→121→91→137→103→155→233→175→263→395→593→445→167→251→377→283→425→319→479→719→1079→1619→2429→911→1367→2051→3077→577→433→325→61→23→35→53→5→1

④数列の一部が合致していない理由

コラッツ予想の本来の定義から導き出される数列（23→35→53→5→1）と、マップから導き出される数列とを比べると少し合致していない部分がある。

合致していない部分は、以下のように黄色マスが斜めに連続している部分（太枠で囲まれている部分）に該当する。

以下のように、この部分を含まれるように拡張することもできるが、本質的に重要ではないので、このまま進めることにする。

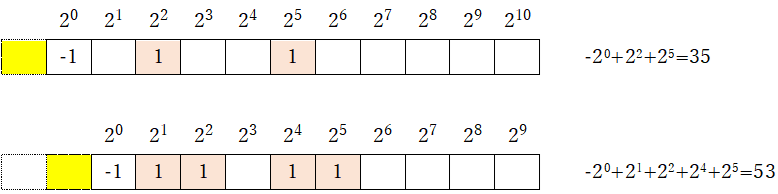
なお、これはあくまで筆者の直感にすぎないが、コラッツ展開の数学的な本質はこのマップから得られる数列であると考えている。つまり、これまでのコラッツ予想（23→35→53→5→1）（「35→53」が入るパターン）は余分な要素が含まれて分かりにくくなっており、それがコラッツ予想の解決を遅らせた原因のように思える（きちんと数学的に説明できる話でもなく、あくまで筆者の直感だが）。

第6章 コラッツ・マップの漸化式

6-1.漸化式の導出（具体的な例）

これまでの説明で、コラッツ・マップについてご理解いただけたと思う。この章では、コラッツ・マップを基にして、以下の漸化式が成り立つことについて具体的な例を用いて説明する。

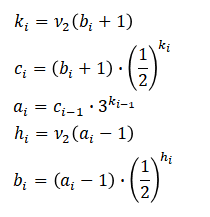
まずは初期値$b_0$（この例では「23」）を設定する。

そして、この$b_0$から「-1」部分を外した数列（太枠で囲った部分）を$c_0$と定義する。なお、この際に指数も振り直すこととする。

このように定義すると、変数$(b_0,c_0)$は以下の関係式で表すことができる。

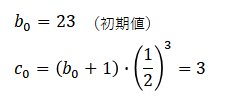
次にマップを下に拡張し、合わせて数字列も最下行までおろすと以下のようになる。

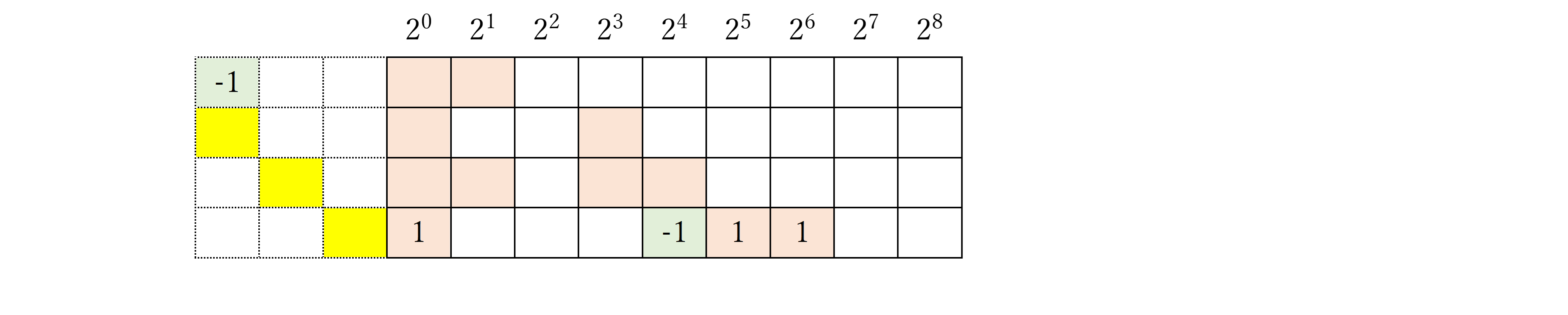
最下行に注目して、以下のような変数$(a_i,b_i,c_i)$を定義する。

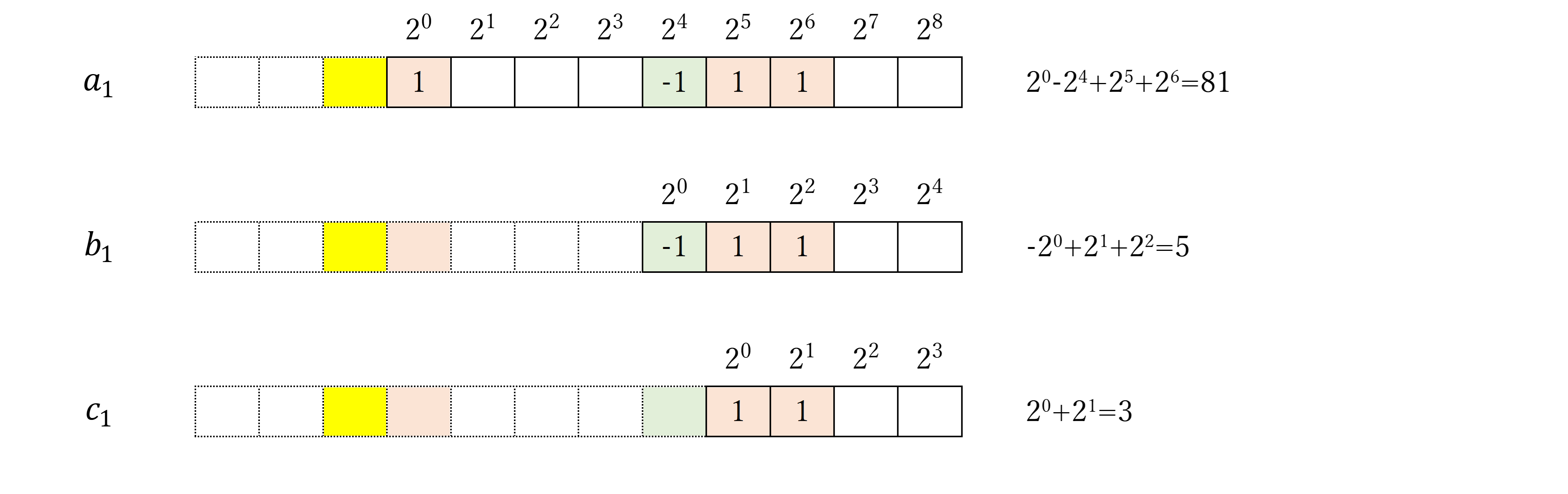
これらの変数$(a_i,b_i,c_i)$をひとつにまとめると以下のような関係となる。

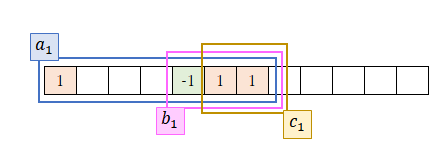
こうして定義した変数$(a_i,b_i,c_i)$は以下の関係式で表すことができる。

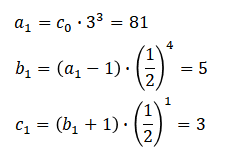
同様の操作を繰り返し、最終的に$b_i$が「1」になるまで続ける。

このとき、変数$(a_2,b_2)$は以下のようになる。（$b_2=1$となるので、$c_2$を定義せず終了となる）

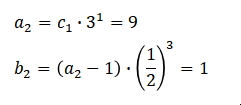
これらをまとめると以下のような関係式になる。

6-2.漸化式の一般化

変数$(a_i,b_i,c_i)$を一般化すると以下のようになる。

なお、初期値23の場合、これらの変数$(a_i,h_i,b_i,k_i,c_i)$は以下のような関係になる。

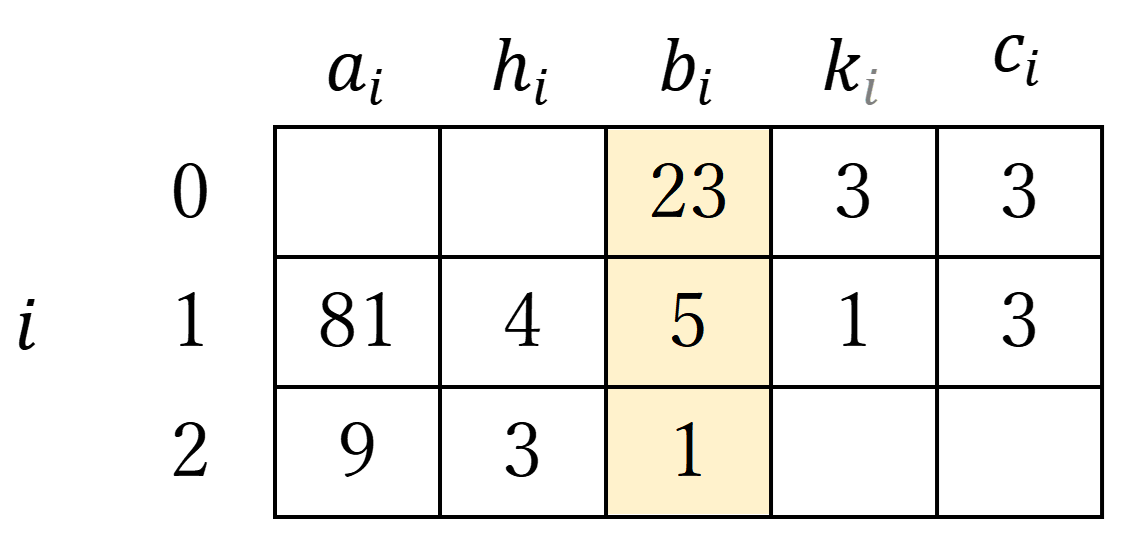
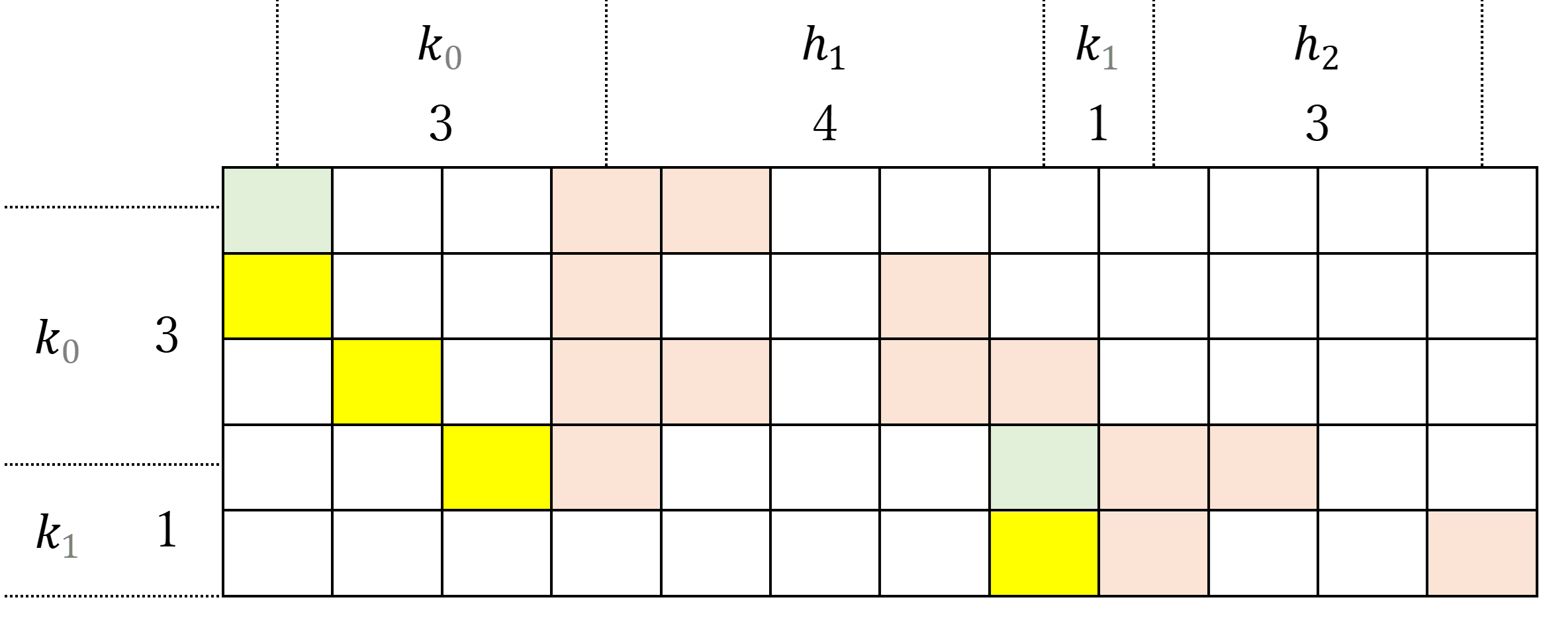
また、変数$(h_i,k_i)$とマップとの関係は以下のようになる。なお、変数$(h_i,k_i)$に関しては、次章でも考察する。

第7章 HK分布

少し長くなったが、前章までで「①コラッツ数列を以下の漸化式を使って表すこと」はご理解いただけたと思う。
続いて検証するのは「②変数$(h_i,k_i)$が以下の『HK分布』に従う」ことである。

そのために変数$(h_i,k_i)$の振る舞いを調べてみよう。 $(h_i,k_i)$の定義は以下なので、どちらも変数$a_i$から計算することができる。

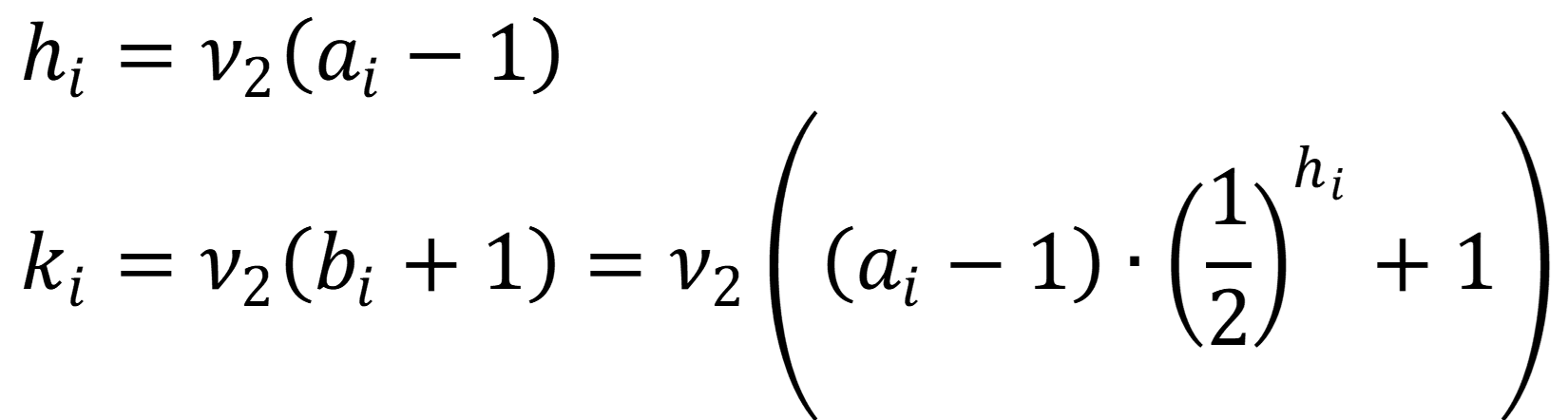
このことは、以下のように、マップ上での$a_i$と$(h_i,k_i)$の関係を考えてみると分かりやすいかもしれない。

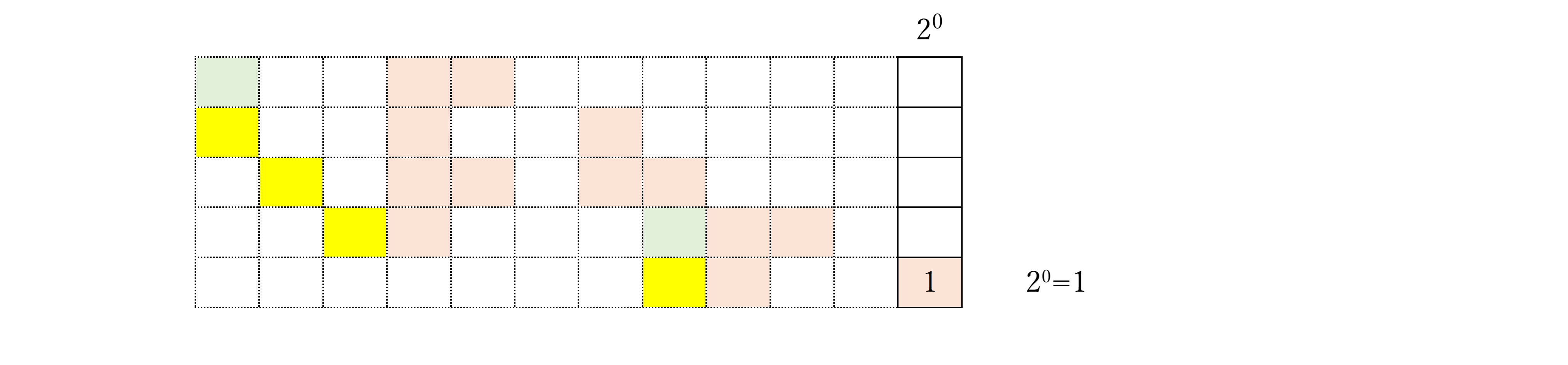
そこで、実際に各$a_i$から$(h_i,k_i)$を計算して、$a_i=3～99999$の範囲での分布を調べてみたところ、以下のような結果になった。これを見る限り、変数$(h_i,k_i)$は$a_i$に関わらず、HK分布に従うと言えそうである。

また、このHK分布は以下の説明からも納得できる話である。

まず、次のようなパターンの数を列挙してみる。ここで、オレンジ色は「1」、緑色は「-1」、灰色は「0または1のいずれか」を表すものとする。

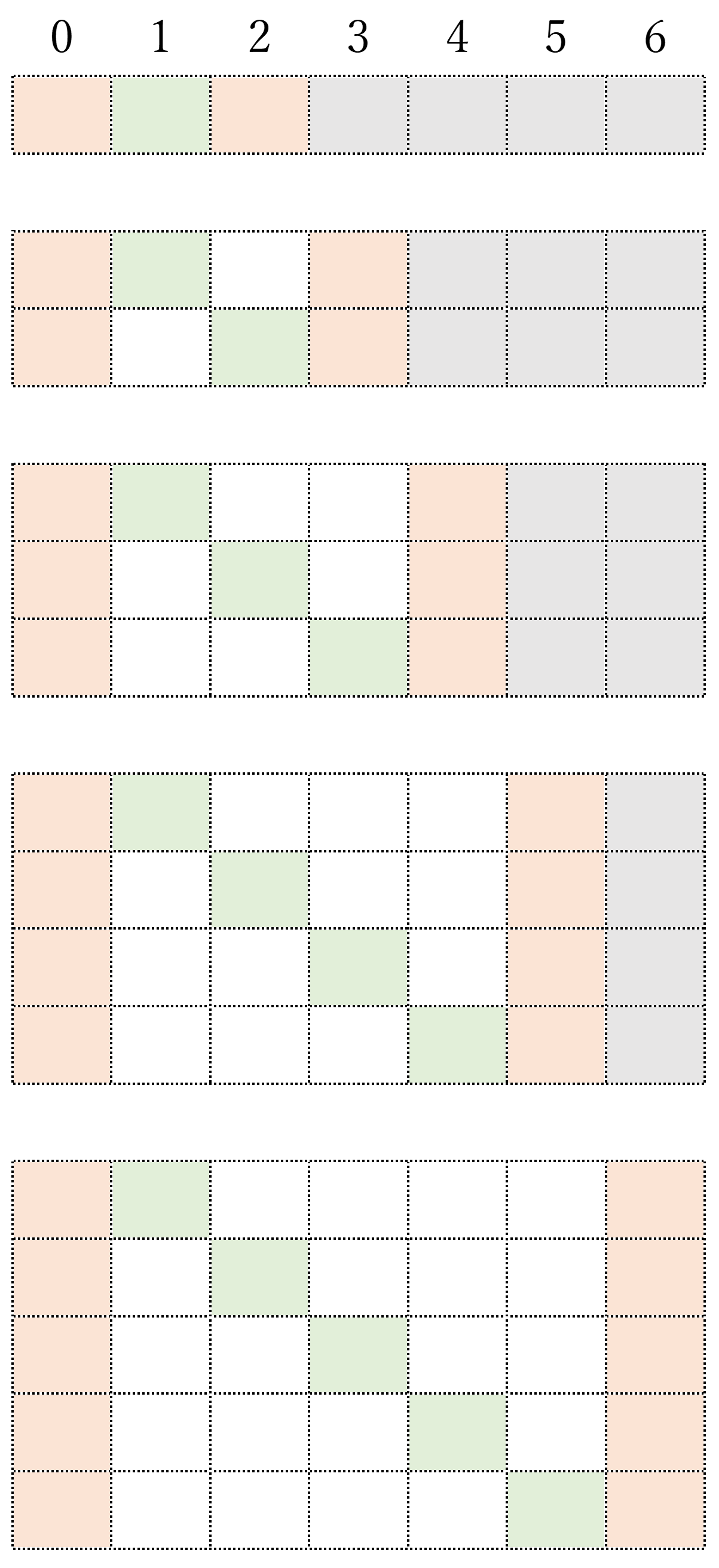
次に、変数$(h_i,k_i)$が取りうる数を考える。すると、灰色セルのみ値が変わるので（0 or 1）、各パターンの取りうる数は（灰色セルの数を$n$として）$2^n$になる。

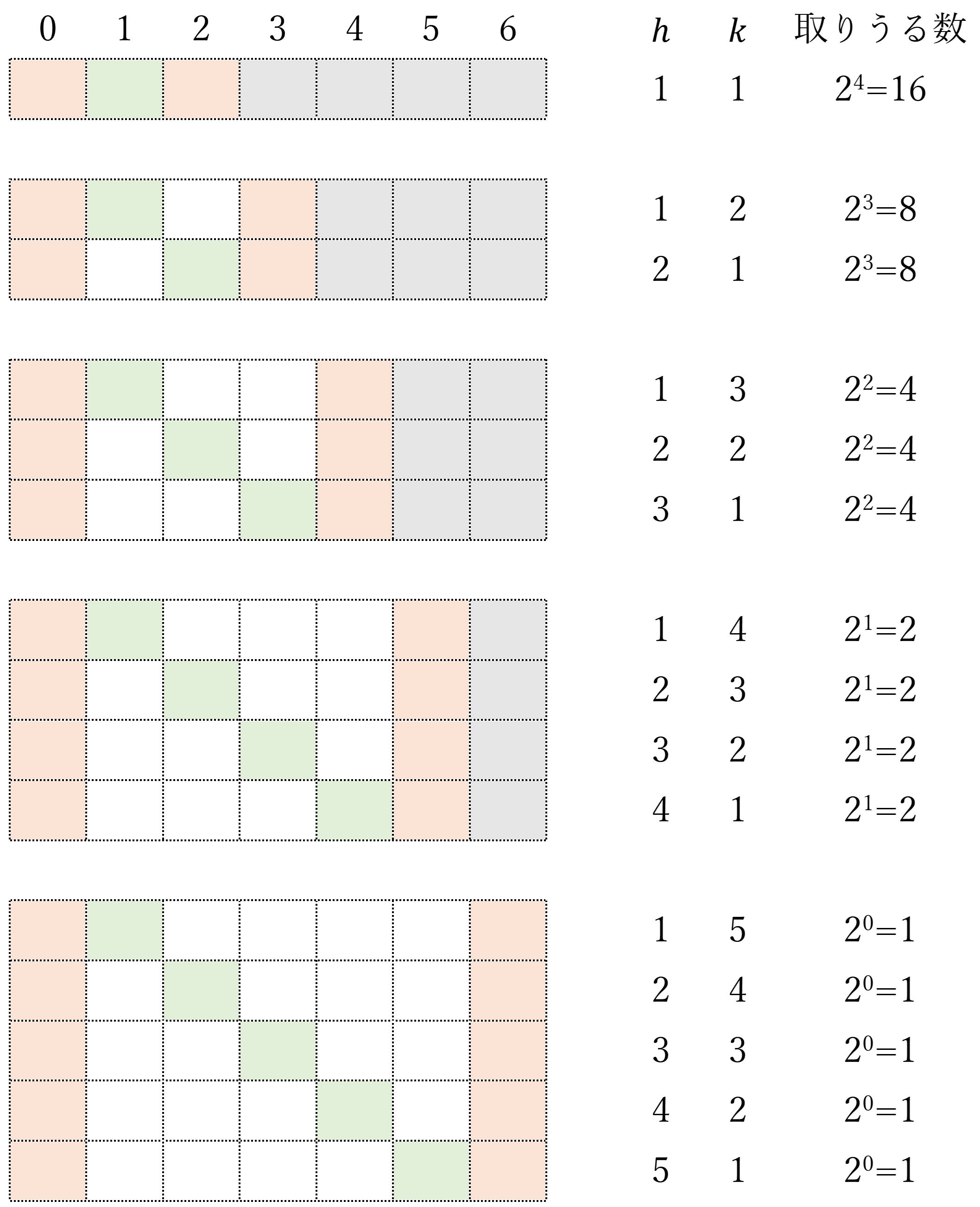
このことから変数$(h_i,k_i)$の分布は以下の通りと考えられ、$n$が十分に大きいとき、HK分布に従うことが分かる。

同様の議論は$k_0$に関しても成り立ち、以下のようにHK分布は適用できると考えられる。

第8章 初期値「27」や「31」のコラッツ展開が大きくなる理由

コラッツ展開には一つの大きな特徴がある。隣接した初期値から始まったとしても展開される数列が似たものになるとは限らず、時には全く異なる様相を見せる場合があることだ。特に、ごく小さな初期値から始まっているにも関わらず、展開した数列が奇妙なほど長く続くものも時々見られる。つまり、コラッツ展開には「初期値がわずかでも異なれば、そのわずかなズレが最終的に大きな違いにつながる」という一種のカオス的な性質が内包されているようだ。

本章では、そうしたカオス的な側面について、少し詳しく見ていきたいと思う。

コラッツ展開を順番に調べていくと、初期値「27」や「31」のように、前後の初期値と大きく異なる振る舞いを見せるものがある。

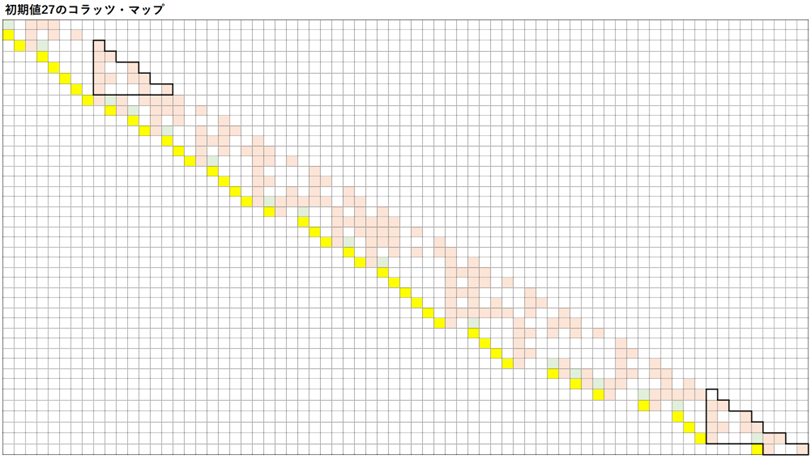
この理由を紐解くために、各初期値（27と31は除く）のコラッツ・マップを表示してみよう。当然だが初期値ごとに描かれるマップは異なっている。しかし、どれも最終段階では似た形になっていることが分かるだろう。

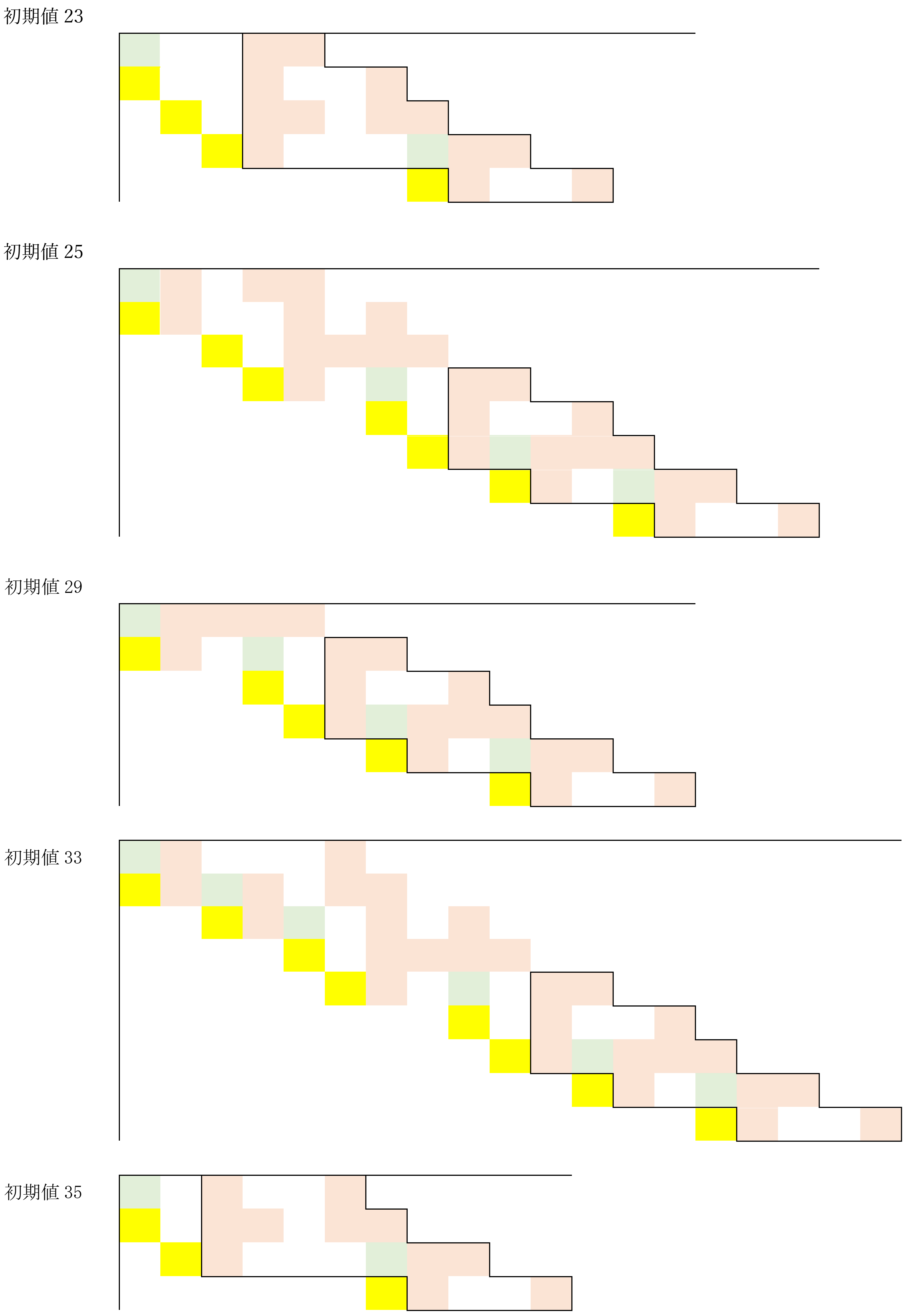
筆者は様々なコラッツ・マップを調べてみたが、ほとんどの場合は上記と同様のパターンで収束していた。全ての初期値で同じようなパターンで終わるかはさらなる検討が必要だが、少なくともこのパターンで終わる場合が多いことは言えそうである。

そこで、この点についてもう少し詳しく調べてみたい。まずは次の3つのパターンから始まるコラッツ・マップを考えてみる。

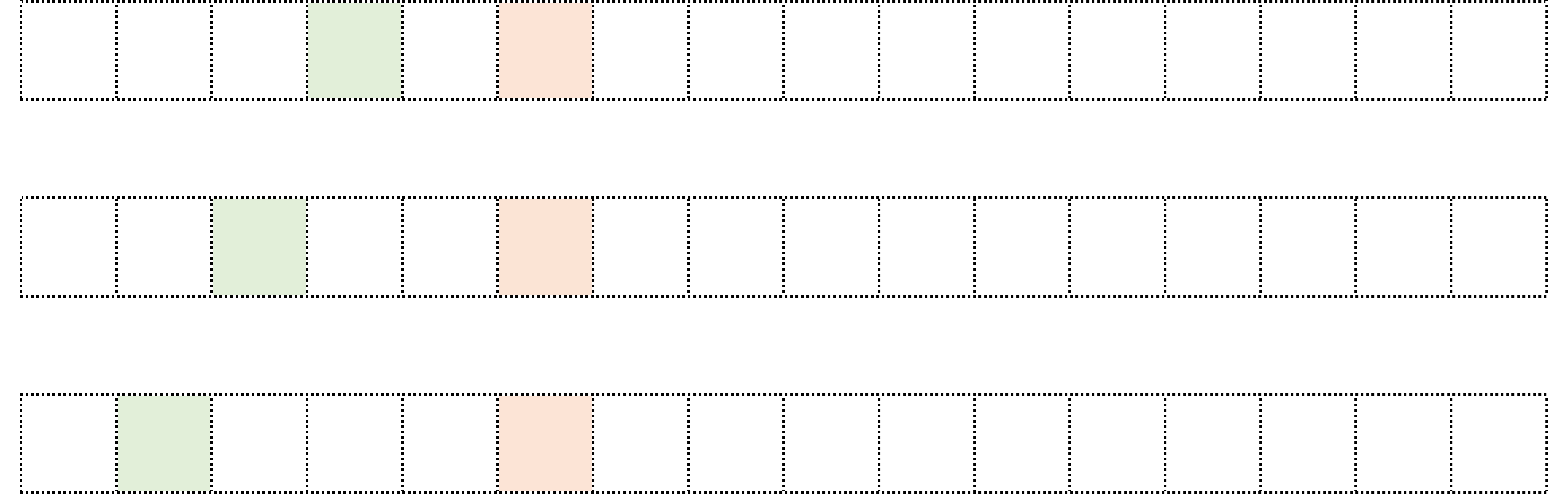
これらのパターンから始まるコラッツ・マップを描いてみると以下のようになり、それぞれ数段階を経て収束することが分かる。つまり、上記の3パターンのいずれかがマップの途中で見つかれば、そこから収束までは「あともう一息」ということになる。

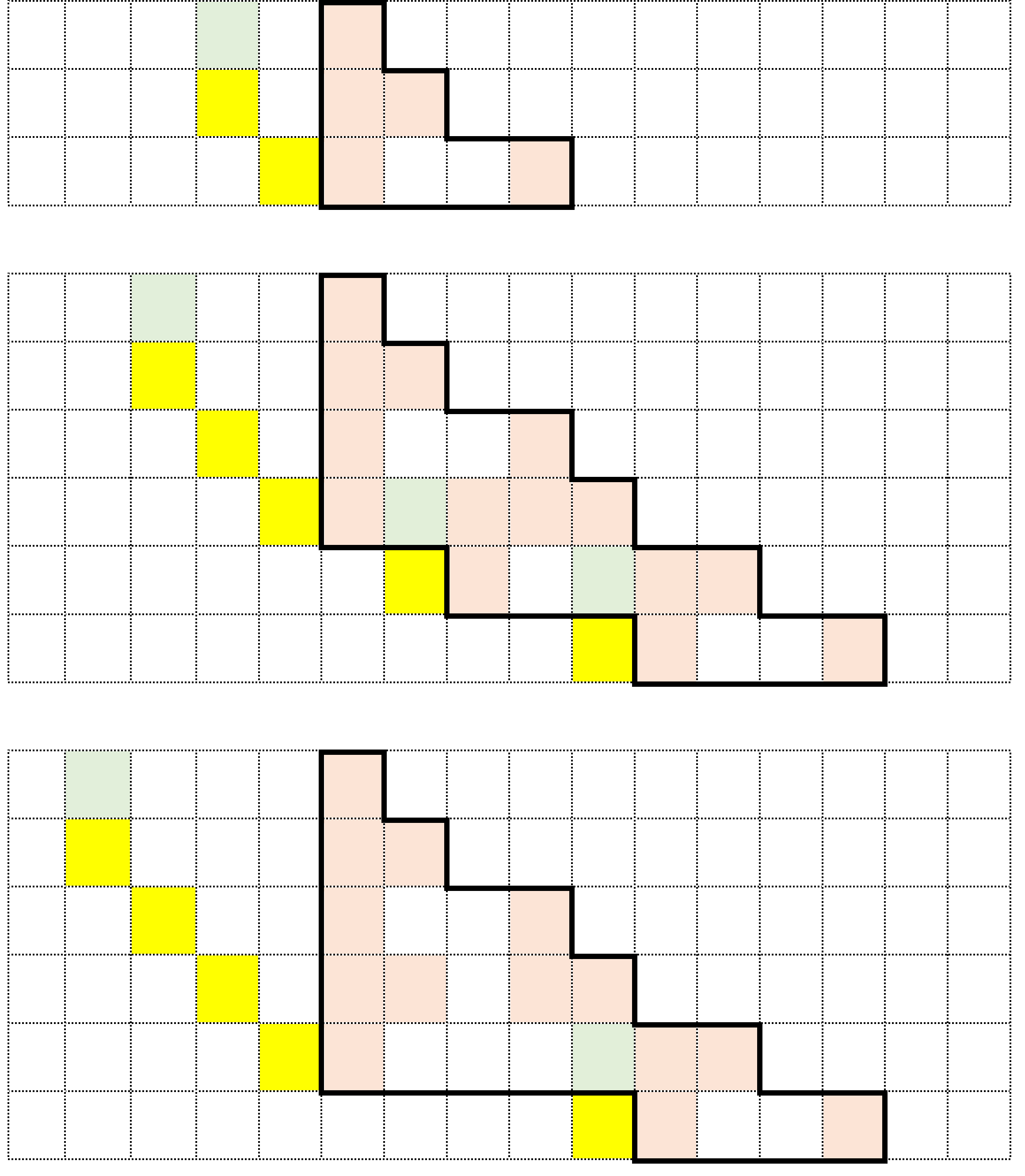
ただ、このようなパターンで始まるマップが直ぐに収束に向かうとは限らない。試しに、上記3パターンよりも、もう一マス間隔が広がった以下のマップを考えてみよう。

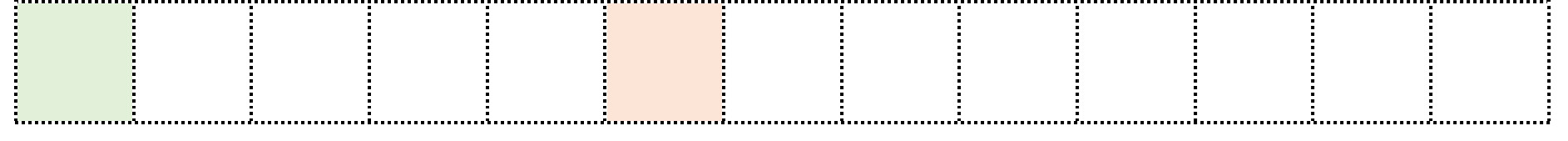
このパターンから始まるマップの場合、途中までは収束するパターンと同様だが、そこで終わらず、以下のように先々まで広がっていくことになる。

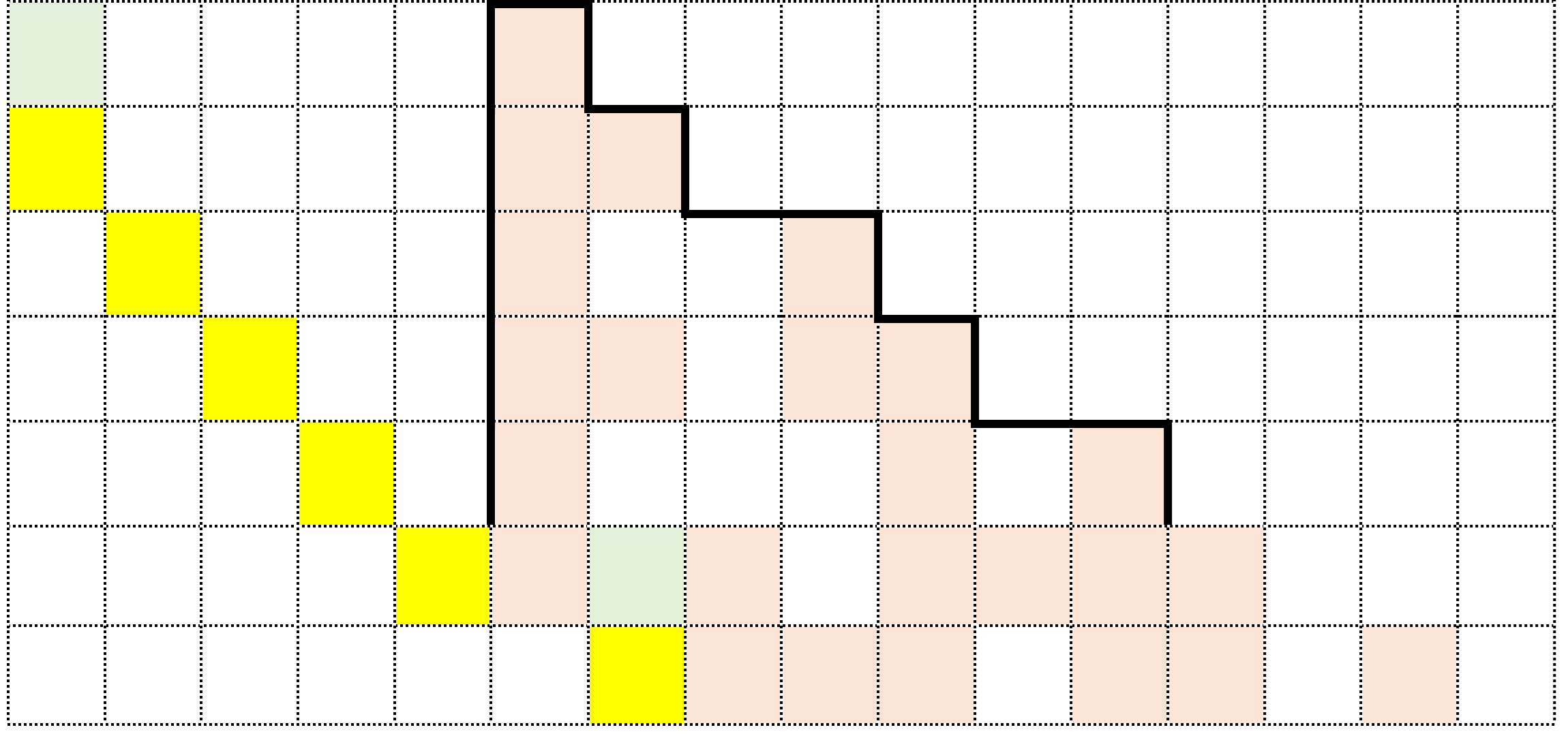
実は初期値が27や31がこの広がっていくパターンに該当する。そのため、この両者では、マップがすぐに収束せず、下に大きく伸びていくことになるのだ。

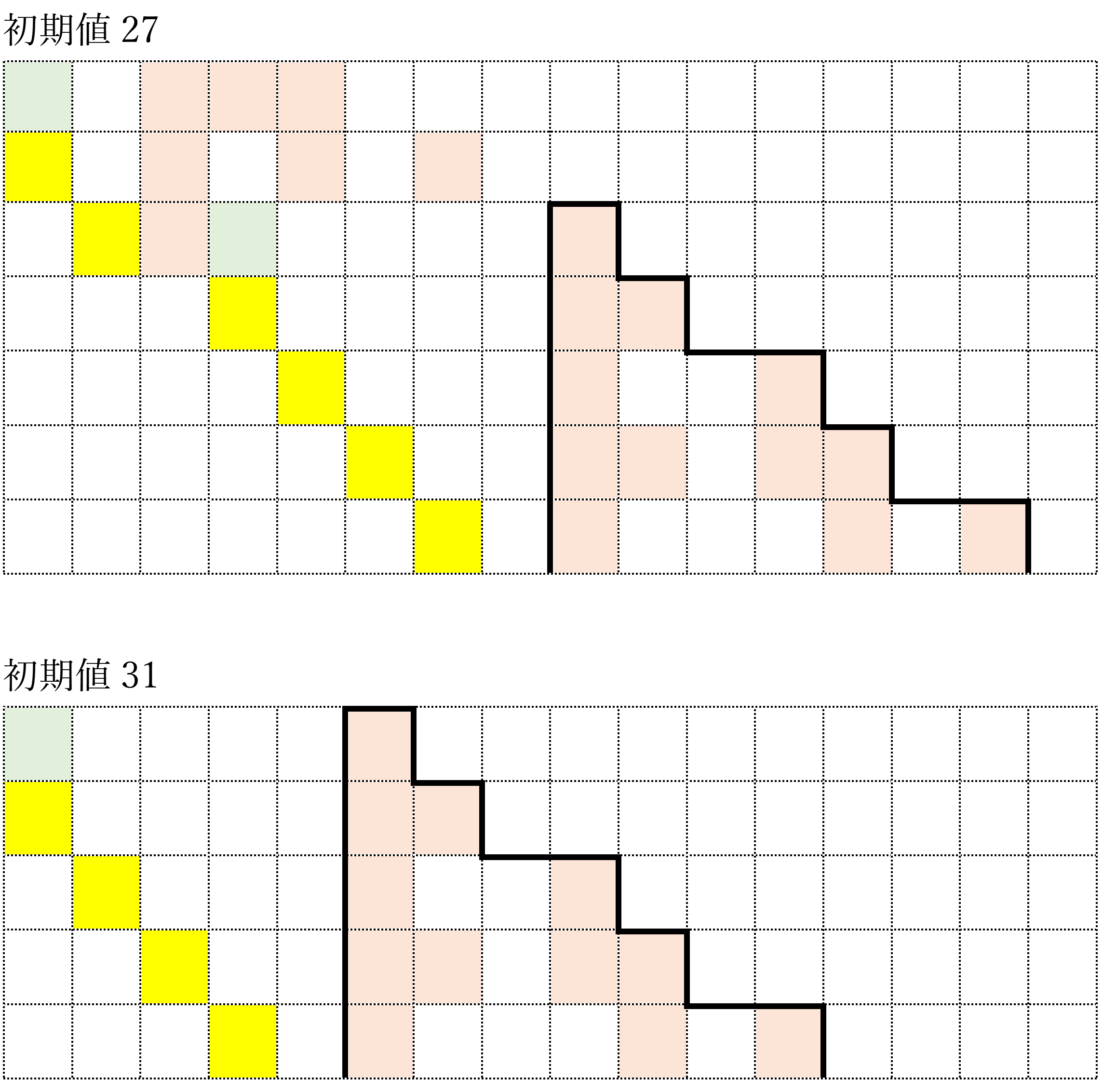
参考までに、初期値が27や31のコラッツ・マップを以下に表す。両マップとも最終的には「収束パターン」を示しているが、いったんは大きく広がっていることが分かるだろう。似たような初期値と思えても、マスの位置が一つ違うとその後の展開が大きく異なることを如実に示している好例と言えるかもしれない。

第9章 終わりに

本稿はこれで終わりとする。筆者は元々物理出身であるので、本稿での議論でコラッツ予想の成立を強く確信できたが、数学の専門家から見れば物足りない点もあるかと思う。

一方で、本稿で用いたアイデアは、手前味噌ながらシンプルかつ網羅的にコラッツ予想の特徴を説明できており、我ながら中々面白い着眼点かなと考えている。本論考に興味を持たれた方は、是非とも論を先に進めていただきたい。