三角法を用いた三平方の定理の証明←JKにできて俺にできないわけないだろ

　どうも、全然ブログを更新しない12匁(ボカロP)です。

　活動してこなかった理由としては、数学以外のことを頑張ってたことも、そもそも数学のほうで芳しい成果を上げられなかったこともあるので、どうかお許しを！！！！

　んで、今回挑戦してみたテーマ、それは、「三平方の定理」です。

　え？　三平方の定理？

　そうです、三平方の定理です。あの、中学生が習う三平方の定理です。

　とにかく、今回は三平方の定理を証明していくんですが、三角法(sinとかcosとか)を用いた証明をしてみました！！

　三平方の定理と三角法について、アメリカのJKがなんかすごいことしたらしいので、JKにできて俺にできないことはないだろ的なノリでやってみたら、できちゃったので紹介します。

　んじゃ、早速本編へレッツゴー！！！！

三平方の定理の証明

　中学校3年生の最後に学習する定理、それは、以下に示す「三平方の定理(ピタゴラスの定理)」だ。

　三平方の定理は、様々な証明方法があり、つい最近(2024年)、三角法を用いた証明が為された。証明の概要は、相似な直角三角形で別の直角三角形の内部を埋め尽くし、級数と正弦定理で式変形して導くものだった。

　話は変わって、高校生になると余弦定理というものを学習する。

　よく考えなくてもわかるが、余弦定理は、三平方の定理の拡張であり、三平方の定理よりも強い。
　つまり、余弦定理を示すことができれば、自然に三平方の定理が示せたことになる。無論、示す過程で三平方の定理を仮定してはならない(過程と仮定())。

　以下、余弦定理を示す。

$0<\theta<\frac{\pi}{2}$ のとき

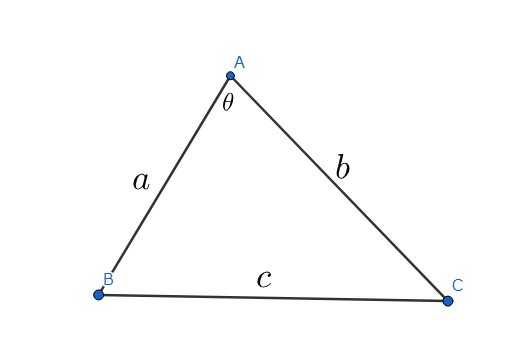考える図

　ここで、$\triangle ABC \backsim \triangle ACD \backsim \triangle CBE$となるような点$D,E $をとる。

D,Eをとる

　このとき、$ AD,BE,CD,CE$を、$a,b,c $を用いて表してみよう。

　$AD=\frac{b^{2}}{a} ,BE=\frac{c^{2}}{a},CD=CE=\frac{bc}{a}$

　この情報を頭に焼き付けてほしい。

　また、もちろん$\angle DAC=\theta$である。

　次に、$BA$の延長上に、$AD=AF $となるような$F $をとる。

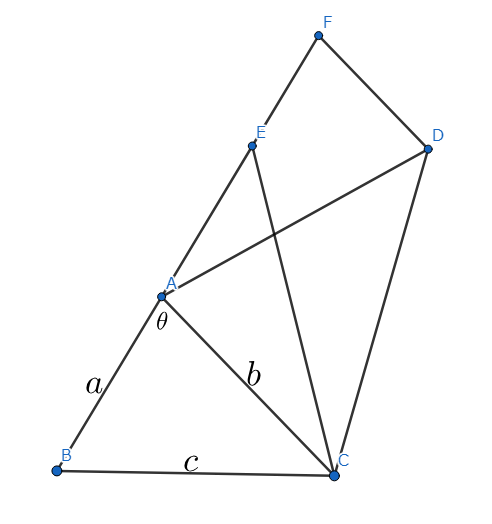Fをとったら二等辺三角形ができる

　$AD=AF$、つまり$AF=\frac{b^{2}}{a}$となったとき、二等辺三角形の底角は等しいため、$\angle AFD=\angle ADF$であり、頂角の外角は$2\theta$だから、

$\angle AFD=\angle ADF=\angle BAC=\angle CAD=\theta$

が成り立つ。よって、$AC /\!/ FD$である。

　続いて、$AB$の延長上に$\triangle ACD \equiv \triangle ACG$となるように点$G$をとり、$GC$の延長と$FD$の延長の交点を$H$とする。

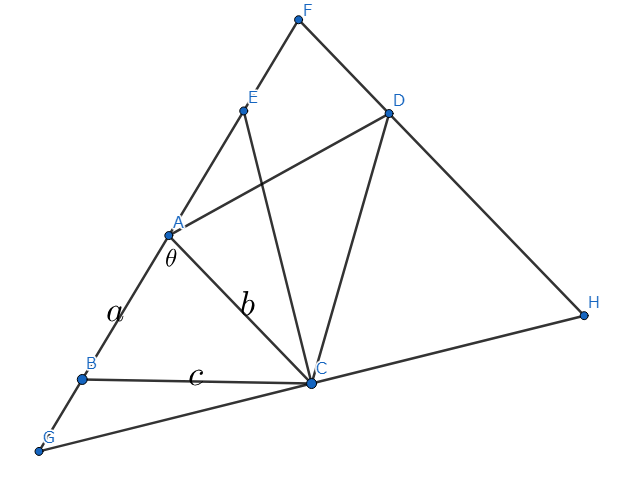GとHを追加

　ここで、合同より$AD=AG$で、$AG=AF$かつ、$AC /\!/ FH$だから、$\triangle GFH$について中点連結定理が使える。よって、

$FH=2b,CG=CH=CD=\frac{bc}{a}$

が成り立つ。

　分かりやすさのため、$EH$を書き足す。

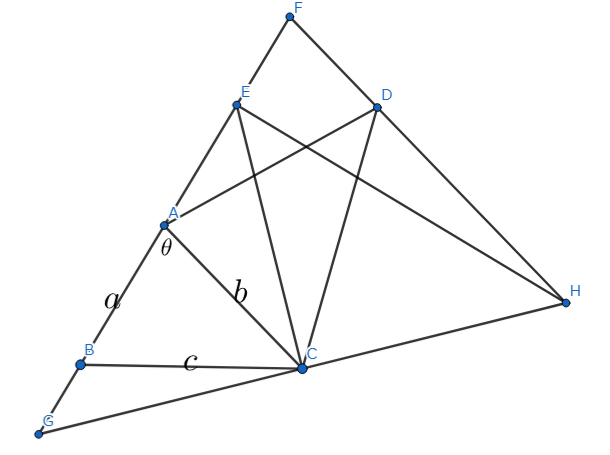EとHを結ぶ

　このとき、$GC=EC=HC=\frac{bc}{a}$より、３点$G,E,H$は、$C$を中心とした円周上にある。$GH$はその円の直径になるため、円周角の定理より
$\angle GEH=\frac{\pi}{2}$すなわち$\angle FEH =\frac{\pi}{2}$が成り立つ。
$FH=2b$と併せると、$FE=2b \cos \theta$が成り立つ。

　今、$BE=AB+AF-FE$が成り立つため、

$\frac{c^{2}}{a}=a+\frac{b^{2}}{a}-2b \cos \theta$,両辺$a$倍して、$c^{2}=a^{2}+b^{2}-2ab \cos \theta$である。

　なんと！余弦定理の一部を三平方の定理を使わずに示せました！
　今回用いた図では、$\theta$ 以外の角も鋭角でしたが、そこは同じ手順を踏めば鈍角でも直角でも成り立ちます。また、$a< c$でも成り立ちます。
　次に、$\theta$が鈍角のときを考えてあげましょう！

$\frac{\pi}{2}<\theta<\pi$のとき

　先ほどと同じように作図をしていくと、$\angle ADF =\pi-\theta$となり、同様の結果が得られます。なお、$\cos (\pi-\theta)=-\cos \theta$となることは、単位円による$\cos$の定義より明らかです。

　しかし！！「同様に」とだけ記しても、楽しくないので、別のアプローチをしてみましょう！

　下のような図を考える。

θがの鈍角の図

　ここで、$\triangle ACD \backsim \triangle A'C'D'$であり、$\theta$が鈍角であるとき$\pi -\theta$は鋭角であるため、$\triangle A'C'D'$に対して余弦定理(鋭角の場合は示した)を使い、整理すると
$\cos(\pi -\theta)=\frac{-a^{2}-b^{2}+c^{2}}{2ab}$すなわち$-2ab\cos \theta=-a^{2}-b^{2}+c^{2}$が成り立つ。
なお、$\cos(\pi -\theta)=-\cos \theta$であることは前述のとおり定義より明らかである。

　この結果を用いて$\triangle ABC$に対し、$a^{2}+b^{2}-2ab\cos \theta$を計算すると$c^{2}$になり、$\theta$が鈍角の場合でも余弦定理が成り立つことがわかる。

　ただし！！！まだ、$\theta=\frac{\pi}{2}$のときが示せていない！！
　さらに！図形を用いて個別に証明すると、それはただの三平方の定理の証明になってしまう！！！

　ここで、極限を用いてはさみうちの定理で鮮やかに解決しようと思う。

　その前に、aとbが固定されているとき、cはθの関数であり、$c(\theta)$が単調増加関数であることを示す。

cとθの関係

• AとBの距離がaである
• Bを中心に半径bの円Bをとる
• Bを中心にABを時計回りにθ度回転させた直線と円Bの交点をCとする。
• Aを中心として、AC=cを半径とした円Aをとる

　当然$\theta'>\theta$をとると、新たにできる交点$C'$は円Aの外側にあるため$c(\theta)$は単調増加関数だとわかる。

　$c(\theta)$が関数であるということは、そもそも$c^{2}$も$\theta$の関数であって、$c^{2}(\theta)$も単調増加関数である。

　ここから、はさみうちの定理に入ります！！！！

　どんな$\theta$に対しても、$2 \left| \frac{\pi}{2}-\theta \right| >\frac{\pi}{2}-\theta$であり、$\theta>\frac{\pi}{2}-2 \left| \frac{\pi}{2}-\theta \right|$が成り立つ。また、$2 \left| \frac{\pi}{2}-\theta \right| >\theta-\frac{\pi}{2}$であり、$\theta<\frac{\pi}{2}+2 \left| \frac{\pi}{2}-\theta \right|$が成り立つ。

　よって、$\frac{\pi}{2}-2 \left| \frac{\pi}{2}-\theta \right|<\theta<\frac{\pi}{2}+2 \left| \frac{\pi}{2}-\theta \right|$が成り立ち、$\theta \rightarrow \frac{\pi}{2}$を考えてみる。

　わかりやすさのため、$\varphi =\frac{\pi}{2}-\theta$とすると、$\frac{\pi}{2}-2 \left| \varphi \right|<\frac{\pi}{2}-\varphi<\frac{\pi}{2}+2 \left| \varphi \right|$で、$\varphi \rightarrow 0$を考えることとする。

　もちろん、$\frac{\pi}{2}-2 \left| \varphi \right|$は鋭角、$\frac{\pi}{2}+2 \left| \varphi \right|$は鈍角であるため、それぞれ余弦定理を使える。

　ここで、$c^{2}(\theta)$は単調増加関数であったため、$c^{2}(\frac{\pi}{2}-2 \left| \varphi \right|)< c^{2}(\frac{\pi}{2}-\varphi)< c^{2}(\frac{\pi}{2}+2 \left| \varphi \right|)$が成り立ち、$\varphi$を正から近づけても負から近づけても$a^{2}+b^{2} \leq c^{2}(\frac{\pi}{2}) \leq a^{2}+b^{2}$が成り立つ。

　よって、$c^{2}(\frac{\pi}{2})=a^{2}+b^{2}$が成り立ち、

　たった今！！！

　$0<\theta<\pi$の範囲で余弦定理が成り立つことと同時に！！

　$\theta=\frac{\pi}{2}$のとき、$a^{2}+b^{2}=c^{2}$が成り立った！！！！

ふぁ～～！！遂に三平方の定理を三角法を用いて証明することができました！！

お疲れ様です！！

まとめ

　もとは、アメリカのJKに負けてたまるかと1週間を捧げて本気になって考えていた証明が、実際に完成して、こうやってブログにかけるのがとてつもなく嬉しいです。だから、若者たちは時間があるうちに、気になったことを探求していって、成果を残していってほしいと思います。
　あと、普通に余弦定理はベクトルの内積とかで証明できるらしいので、この証明はたいして美しくなさそうです。残念...なんで証明した後に気が付くんだ...。
　ともかく、このブログを通して、少しでも参考になった人がいれば、それで十分です。特に、極限とかを除けばほぼ中学3年生で習うことをベースに証明を構成したので数学に詳しくない人でも読みやすかったのではないかと思います。
　それでは、またどこかで！！