34! mod(2^32) ≡ 0は正しいか？　また、34!なのは偶然か？

前書き

C言語で、入力した値の階乗を出力するプログラムを作っていた。
(出力はsigned int型、オーバーフローを考慮しない)

値を変更して結果を確かめていると、入力が34以上のときに出力が0になることが分かった。

入力:33 出力:2147483648
入力:34 出力:0
入力:35 出力:0
...

急に出力が0となったため、この結果は正しいのか、
出力が0になるのがn=34以降なのは何か意味があるのかどうか気になったので、検証してみる

Excelで再実験

C言語において、算術オーバーフローは 未定義動作を引き起こす。
上記の結果も未定義動作によるものの可能性があるため、Excelで実験をしてみる。

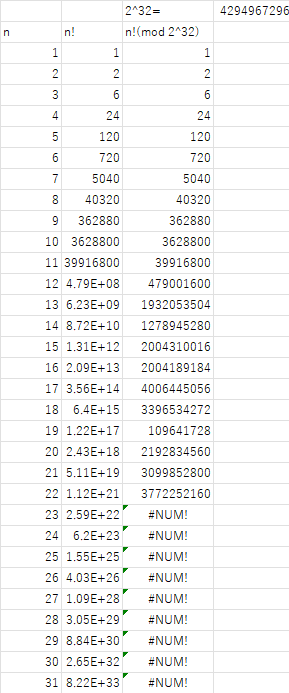Excel計算その1

$23!\ (\bmod 2^{32})$を実行する部分で!NUMエラーが発生してしまった。

どうやら このサイトによると、
$a\gg b$のとき、$a\ (\bmod b)$を実行するとエラーになってしまうらしい。
というわけで、ここからは合同式の性質を利用することにする。

公式1を用いて、
$22!\ (\bmod 2^{32}) \equiv 3772252160$
$23!\ (\bmod 2^{32}) = 23\times22!(\bmod 2^{32}) \equiv 23\times 3772252160 \equiv 862453760$
$24!\ (\bmod 2^{32}) = 24\times23!(\bmod 2^{32}) \equiv 24\times 23\times 3772252160 \equiv 3519021056$
$...$
という風に計算できる。

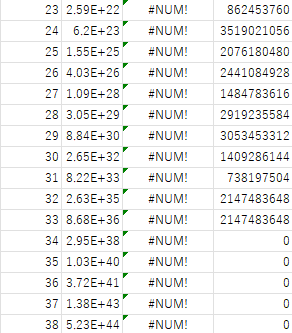Excel計算その2

$34!$以降、modの計算結果が0になることが確認できた。

ここであることに気づく

modの定義を思い出す。

この定義を逆向きにしたものにタイトルの数式を代入すると、

$34!\quad (\rm{mod}\space 2^{32}) \equiv 0 \Longleftrightarrow$$34!$を$2^{32}$で割った時のあまりが$0$

あまりが$0$ということは、除法の原理より、$k$をある整数として
$$\frac{34!}{2^{32}}= k $$ と表せることになる。
これで$\frac{34!}{2^{32}}=\rm{整数} $は成り立つことが証明されたが、
念のため、これを別の方法で証明してみる。

証明

分数の性質より、ある分数を約分したものは元の分数と等しい。
分母は2の累乗のみで構成されているから、約分をするためには
$34!$の素因数にどれだけ2が含まれているかを考えればよい。

階乗の定義から、$1\sim34$までの整数において、2を素因数に持つ整数を列挙すると、
$\{2,4,6,8,10,12,14,16,18,20,22,24,26,28,30,32,34\}$
それぞれの整数に含まれている素因数2の個数は
$\{1,2,1,3,1,2,1,4,1,2,1,3,1,2,1,5,1\}$
全部足すと$32$。

以上より、
$34!$の素因数には$2^{32}$が含まれていることが分かった。
よって、素因数分解の性質より
$34! = 2^{32} \times \rm{整数}$と表すことが出来るので
$$\frac{34!}{2^{32}}= \frac{2^{32} \times \rm{整数}}{2^{32}}= \rm{整数} $$
以上より、$$\frac{34!}{2^{32}}= k $$は成り立つ。

結果

$34!\quad (\rm{mod}\space 2^{32}) ≡ 0$が成り立つことを証明できた。
そして、$n\geqq34$で出力が0になることも理解できた。
なぜなら、$n!$の$n$の値を増やすにつれ、$n!$に含まれる2の素因数が増えていき、
それが32個を超すのが$n=34$のときであったからである。
($34!=2^{32} \times \rm{整数} \Longleftrightarrow 34!は2^{32}の倍数\Longleftrightarrow 34!は2^{32}で割り切れる \Longleftrightarrow 34!\quad (\rm{mod}\space 2^{32}) ≡ 0$)

おまけ

$n!$にどれだけ2の素因数が含まれるかを表す数列は OEIS(A011371)に存在する
これによると、$n!\rm{に含まれる2の素因数の値=a(n)}$と置くと、
$$a(n) = \sum_{k=1}^{\lfloor \frac{n}{2} \rfloor} \lfloor \log_2\biggl(\frac{n}{k}\biggl)\rfloor$$
と表せられるらしい。