JMO2024予選第６問の三角関数を用いた解法

JMO2024予選第６問を三角関数を用いて解いてみました．また今回用いる手法は個人的にかなり汎用性の高いものだと感じているので是非参考にして頂きたいです．

解法の流れ

今回の解き方について軽く説明すると，

• Step1.適当に角$\alpha,\beta,\cdots$を定める．
• Step2.角度追跡をして図に登場する角を$\alpha,\beta,\cdots$で表す．
• Step3.正弦定理を用いて$\alpha,\beta,\cdots$の関係式を導く．
• Step4.出来た関係式から欲しいもの($\sin\alpha,\cos\beta$など)を求める．

といった感じになります．

解説

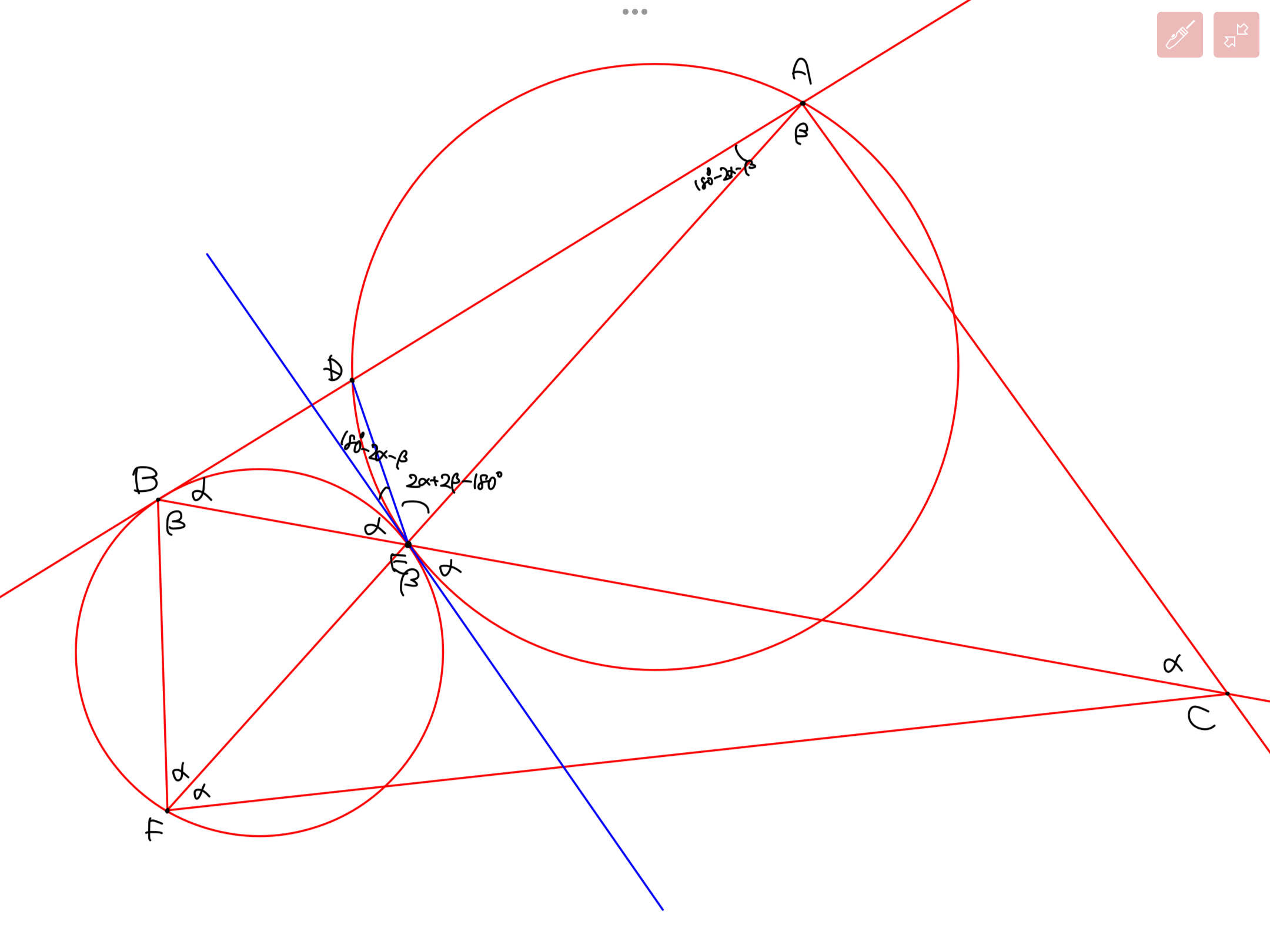図
$\alpha=\angle ABC,\beta=\angle CBF$(Step1.)として，円周角の定理や接弦定理を用いて角度追跡を行った結果が上図となります(Step2.)．円$\omega$，円$ADE$の共通接線を引いた理由は接する条件を使いたいからです．
さて，正弦定理を$\triangle ADE,\triangle ABE$に用いると
$$\frac{AD}{\sin (2\alpha+2\beta-180^{\circ})}=\frac{AE}{\sin\beta},\quad \frac{AE}{\sin \alpha}=\frac{AB}{\sin(\alpha+\beta)}$$
がわかり，これより，
$$\frac{3}{\sin (2\alpha+2\beta-180^{\circ})}=\frac{5\sin \alpha}{\sin \beta \sin (\alpha+\beta)}\quad\cdots(1)$$
がわかります．一方，正弦定理を$\triangle CEF,\triangle CEA$に用いると，
$$\frac{CF}{\sin (\alpha+\beta)}=\frac{CE}{\sin \alpha},\quad \frac{CE}{\sin \beta}=\frac{AC}{\sin (\alpha+\beta)}$$
がわかり，これより，
$$2=\frac{\sin \beta}{\sin \alpha}\quad \cdots (2)$$
がわかります．
以上より未知数2個に対して式が2つ立ったので$\alpha,\beta$が決定できるはずです(Step.3)．
求めるものを$\alpha,\beta$で表しておきます．正弦定理を$\triangle ABC$に適用すると$\frac{BC}{\sin2\alpha}=\frac{AB}{\sin\alpha}$となり，$BC=10\cos\alpha$がわかります．

さて，(1)を整理すると，$\frac{3}{-2\cos(\alpha+\beta)}=\frac{5\sin\alpha}{\sin\beta}$となり，(2)と併せて$\cos(\alpha+\beta)=-\frac{3}{5}$がわかります．ここで$s=\sin\alpha$とおくと，$\cos^2\alpha=1-s^2$，また(2)より$\sin\beta=2s$となり，更に$\cos^2\beta=1-4s^2$となります．
$\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta$に注意すると，
$$\cos\alpha\cos\beta-2s^2=-\frac{3}{5}$$
$$\cos\alpha\cos\beta=2s^2-\frac{3}{5}$$
$$(1-s^2)(1-4s^2)=(2s^2-\frac{3}{5})^2$$
$$4s^4-5s^2+1=4s^2-\frac{12}{5}s^2+\frac{9}{25}$$
$$\frac{13}{5}s^2=\frac{16}{25}$$
$$\therefore s^2=\frac{16}{65}$$
と計算出来ます．よって，$\cos^2\alpha=1-s^2=\frac{49}{65}$であり，$\alpha$が鋭角であることに注意すると$\cos\alpha=\frac{7\sqrt{65}}{65}$となります(Step4.)．
以上から，$BC=10\cos\alpha=\frac{14\sqrt{65}}{13}$がわかります．

おわり

いかがでしたか．今回用いた手法が良いと思ったら是非他の問題でも試してみてください．ここまで読んで頂きありがとうございました．