CpSL 参加記

初めに

どうも,nhodkseWです。今回は4/26の9:00〜4/27の16:30までポロロッカ上で行われた【CpSL by Weskdohn】の感想などを書いていこうと思います。
このコンテストは、聖光学院数学研究会が配布している「チャレンジ問題」に出題しようと、Weskdohnさんが作問した問題で構成されているらしいです。
問題ページは以下です。Weskdohn，同じ学校ですが,あんまり面識ないですね。
CpSL by Weskdohn コンテストページ

参加時の動き

点数はすべて100点。とりあえず前から解いていくことにしましょう。
pororoccaはｒateなぞないので……。

Practice (正答者14人,正答率14/14=100.0％)

CpSL Practice
去年の7/16、丁度T・Rくんという友達の誕生日だったので急遽作問した問題らしいですね(友達談)。
179の倍数で1231以下のものは幾つかありますが,7/16だけがありうるというのはかなり面白いと思いました。
ということで答えは7/16です。あの野郎,回答形式汚くしやがって…

A (正答者13人,正答率13/47〜27.6％)

CpSL A問題
元々はペナ誘発問題としてOMCに提出した不採用問題らしい(7月くらいに作ったそう)
まず,a,bの範囲が整数ですね。スコア=2って案外少ない…？と思いながら考えると,これab=(-a)(-b)やん！
つまりabが素数になればいい。素数表から,答えは796！
あれれ？色々おかしいぞ…？(コナン風)
答えが違うそうなのでよくよく考えると……a≦bですね。N=1も条件を満たします。
なので答えは797です。
Weskdohn曰く「結構ペナってて目論見は成功かな…聖光だけに」だそうです。うるせぇ。

B (正答者12人,正答率12/23〜52.1％)

CpSL B問題
計算ミス無く解けるかな〜という問題ぽいですね(8月頃作問したそうです。)
ある桁位MについてCという数が使われたとすると、M以外の桁に用いられた数の組み合わせは,4!=24通り.Cとして考えられるS,K,G,6,5,それぞれの10進法での値は,28,20,16,6,5です.
Mとして,290,291,292,293,294の5通りが考えられるので,24×(28+20+16+6+5)×(290+291+292+293+294)を計算すれば良く、結果1318573800を答えとして得ます。
そこまで難しくないかなーと思いましたが、順位表を見る限り、刺さる人には刺さっていたみたいです。(要するにペナ誘発問題と化していた)
これで僕とWeskdohnの学校名＆学年が割れるのは仕方ない

C (正答者13人,正答率13/13=100.0％)

CpSL C問題
この問題はもともと、数学嫌いの友達向けに作問したそうです。(友達喜んでました。9月くらい？)
最初はスコアが偶数になるような置き方を求めさせていたそうですが、この場合どう石をおいても必ず正解になるみたいです。凄いですね〜
答えは何種類かあるみたいですが,僕の解答は以下です。
10100 01100 11011 00110 00101

D (正答者11人,正答率11/11=100.0％)

CpSL D問題
JJMO前に期待値の絡んだ問題を作りたいなーと授業中に数式を弄くっていて思いついたそうです(本人談)。
実際に聖光の文化祭ではチャレンジ問題がある程度解けた人にダイスを配布しています(ぜひぜひ来年以降getして下さい)
さて、それぞれのダイスの出目の期待値を計算してみましょう。
あるsについて、出目の期待値は$\dfrac{ \sum_{i=1}^{10} a_k^{s+1}}{ \sum_{i=1}^{10} a_k^{s}}$で計算できます。これをそれぞれかけ合わせると、分母と分子が上手く消えるので、結果$\dfrac{ \sum_{i=1}^{10} a_k^{11}}{ \sum_{i=1}^{10} a_k}$を計算すれば良いです。
分母と分子が上手く消える問題っていいですよね〜
まあまあ難しいかなと思ったのですが、かなり解かれていてびっくりしました。

E (正答者4人,正答率4/23〜17.3％)

CpSL E問題
ゲームに関する問題を作ろうと作問した問題みたい(1月ごろ？)
AとBに分けて考えます。
Aについて、$\dfrac{1}{2}$であることがわかります。(先手必勝です。証明は簡単なのでやってみてください)
問題はBです。マス目を以下のように分けます。
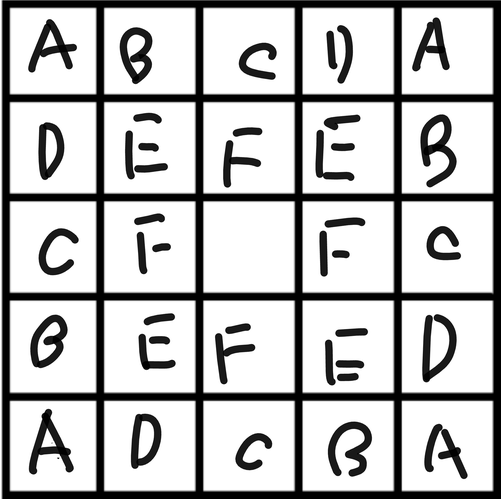紐づけ
12個の置き方は(1)360°回転して重なる場合,(2)180°(略),(3)90°(略)に分けられるので、余事象などを用いて計算すると,答えは$\dfrac{1}{2}\times1300316=650158$とわかります。
やっぱりBが鬼門だったようで、正答率は最低みたいです。マスと記号を紐づけるのは意外に有用ですので覚えておくといいかもしれませんね。
Weskdohnは想定解が合っていて安心してました(ちゃんと確認しろよ馬鹿)

F (正答者10人,正答率10/10=100.0％)

CpSL F問題
虫食い算ですね！実際のチャレンジ問題よりは簡単でした。(作問時期は7月だそう.案外早いのね)
O→S→K→E→N→I→Uの順に埋めていくのがいいですかね。答えは27894です。
(彼曰くこの問題、没にした理由があるそうで……数研にskg65がWeskdohnと僕しか居ないんですね……よって作問者がほぼバレてしまうと.いやお前profileに書いとるやないかい)

G (正答者12人,正答率12/20=60.0％)

CpSL G問題
レピュニット数……きれい。
実はこれだけ作問時期が早いらしく．去年の3月みたいです。(中2の時！)
解き方は様々ありますが,例えば,
$R_2×101010101010101010101010=R_{24},R_3×100100100100100100100100=R_{24},R_4×100010001000100010001000=R_{24}$
…等の事実を用いることで導くことが出来ました.
$R_{24}=3⋅7⋅11⋅13⋅37⋅73⋅101⋅137⋅9901⋅99990001$ (ちなみに24は,2024の下2桁から取ったそう)ですので答えは100000284です。
実は僕,レピュニット数には思い入れがあって……中１の頃の幾何の先生が「ポッキー数」という名前で紹介していたのがすごく記憶に残っています。(「プリッツ数は？と文句を言わないように」―という注意書き……懐かしいですね)
ありがとうWeskdohn（）

H (正答者4人,正答率4/6〜66.6％)

CpSL H問題
今年の1月くらいに作問してOMCに提出した不採用問題みたいです。
目で解く幾何に類題が載ってたような記憶も……。途中からコンテストに加えられていたので正答者は少ないですね。ちゃんと確認しておいて良かった。
有名性質として、$\sqrt{ab}=2025$が成り立ちます。(2025はこの問題文においての値です。理由は練習問題として置いておきます)
よってこれは$2025^2=3^8\times5^4=ab$となるa,bの組の個数を求めることと同値です。大小関係が定まることに注意すれば、求める答えは$\dfrac{9\times5-1}{2} +1=23$から23通りと分かります。

I (正答者12人,正答率12/12=100.0％)

CpSL I問題
チャレンジ問題用に作問したものの、問題として大丈夫か不安になってCpSL行きとなった問題だそう。(12月くらい,答えがたくさんあるので採点が大変そうね)
解説はできっこないので省略しますが……小学生なんかはかなり好きそうな問題ですね。特に答えが定まっているわけではないですし……。
（Weskdohnからの言伝:一例として挙げた式が綺麗すぎたかもです,すみませんでした）

J (正答者9人,正答率9/14〜64.2％)

CpSL J問題
入試予想問題用に作問した問題かな…？(募集時期からして,１月くらいに作ったのかな)
引いた枚数は$2\times13<31$から明らかに3枚です。
引いた値をMIN順にA,B,Cとすると、$11< C<13$がBを考えることでわかります。この時ABCの範囲は714<ABC<1299となるので、1001,1010,1110のどれかになります。それぞれを分解すれば(7,11,13),(10,10,11)が答えとわかります。
ミスっている人は片方忘れていたのかな？入試は一度きりなのでよく見直しましょう()←一発正解だからって自惚れすぎ

K (正答者5人,正答率5/17〜29.4％)

CpSL K問題
出ました最難関。この問題を出すためにCpSLを作ったと言っても過言ではないそうです(過言だろ)
答えを一から書くとめんどくさいので楽をします。こちらを御覧ください。
ほぼ答えのサイト
求める値は対角線の$66$乗和ですから,ページにある値を$33\times66^{66}$倍したものが答えです。(よく知ってたな,僕)
実際これを計算すると$586065959427313424570600679270220475025051017407877083853741077765190776467862520537931152381910389823959161200660336658656676755348589117440\times 33$となり，これを2025で割った余りは$1620$です。
後輩によると複素数平面で頑張るとsinの計算に帰着され、円分多項式を駆使すれば答えが出せるそうです。えぐいな。
作問時期が11月だったので,66が11の倍数になることに若干興奮していたそう(え？)

L (正答者8人,正答率8/13〜61.5％)

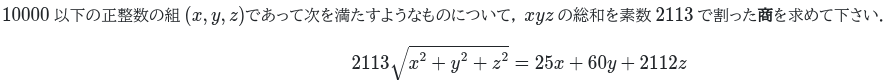CpSL L問題
これまた綺麗な問題ですね。2が多いですし,2月くらいに作問したのかな…。
$25^2+60^2+2112^2=2113^2 $であることに気がつけば、コーシーシュワルツを使うことで,x:y:z=25:60:2112がわかります。10000以下の範囲でこれを満たすxyzの総和は,$(25×60×2112+50×120×4224+75×180×6336+100×240×8448−23)÷2113$から$149929$です。
後輩によるとチャレンジ問題に出せばいいのにーとのこと。聞いてるかWeskdohn？

M (正答者12人,正答率12/17〜70.5％)

CpSL M問題
見た目からベズーの定理味がプンプンしますが,これもOMC不採用問題みたいです。(2月くらい)
gcd(131560,133650)=110ですから,ベズーの定理より110が答えです。
流石に定理そのままじゃないか？

結果

全完1ペナで1位でした！OMCではないにせよ,一位は嬉しいですね。
ではまた……

ってのは全部ウソ

真面目に読んでくださっていた０割の読者様、すみません。
どうもWeskdohnです。茶番に突き合わせて申し訳ないです。simasimaさんやzplcさんがこういうのやってて真似したくなりました。
ちなみにNhodksewという名前はWeskdohnを逆にしただけです。
来年,CpSL第二弾やりたいですね〜でも数研チーフなので難しいかも…？頑張ります。