三角関数の最大・最小問題と指数関数・対数関数の最大・最小問題
記号の解説
まずは高校の教科書では見慣れない記号の導入をするが, 問題の解説を見ながら確認してくれればよい。
$\mathbb{C}$:複素数全体の集合
$\mathbb{R}$:実数全体の集合
$\mathbb{Q}$:有理数全体の集合
$\mathbb{Z}$:整数全体の集合
$\mathbb{N}$:自然数全体の集合
有界閉区間:$[a, b]=\{x\in\mathbb{R}; a\leqq{x}\leqq{b}\}$
有界開区間:$(a, b)=\{x\in\mathbb{R}; a<{x}< b\}$
半開区間:$(a, b]=\{x\in\mathbb{R}; a<{x}\leqq{b}\}$
半開区間:$[a, b)=\{x\in\mathbb{R}; a\leqq{x}< b\}$
無限開区間:$(a, \infty)=\{x\in\mathbb{R}; a<{x}< b\}$
無限開区間:$(-\infty, b)=\{x\in\mathbb{R}; a<{x}< b\}$
無限閉区間:$[a, \infty)=\{x\in\mathbb{R}; a<{x}< b\}$
無限閉区間:$(-\infty, b]=\{x\in\mathbb{R}; a<{x}< b\}$
これらと$\mathbb{R}=(-\infty, \infty)$を総称して区間という。
集合$A, B $から新たな集合$A-B$を
\begin{align*}
A-B=\{x;x\in{A}かつ, x\notin{B}\}
\end{align*}
で定め$A$から$B$を除いた差集合という。とくに$A$が普遍集合(考えている集合の中で最大の集合)のとき, これを$B^{c}$と書き$A$における$B$の補集合という。
高校では$A$の補集合を$\overline{A}$で書くのが一般的だが, 本当は$\overline{A}$は閉包の意味でとられるのが普通である。大学では, 補集合は$A^{c}$と書く。今回は普遍集合を$\mathbb{R}$とおいているので
\begin{align*}
A=\{x\in\mathbb{R};x\geqq{0}\}
\end{align*}
なら
\begin{align*}
A^{c}=\{x\in\mathbb{R};x<0\}
\end{align*}
である。
$P(x)$を$x\in{X}$の条件とする。
\begin{align*}
\forall{x\in{X}}, P(x)
\end{align*}
を「任意の$x\in{X}$に対して, $P(x)$である」と読む。また
\begin{align*}
\exists x\in{X}, P(x)
\end{align*}
で「$P(x)$となる$x\in{X}$が存在する」とか「ある$x\in{X}$を用いて$P(x)$と表される」と読む。$\forall$を全称記号, $\exists$を存在記号といい, ふたつ合わせて量化記号という。
\begin{align*}
\forall x\in\mathbb{R}, x^{2}\geqq{0}
\end{align*}
を「任意の$x\in\mathbb{R}$に対して, $x^{2}\geqq{0}$である」と読む。
$y$が2の倍数であるとは,
\begin{align*}
\exists{x\in\mathbb{Z}}, y=2x
\end{align*}
が成り立つことである。これを「$y$が2の倍数であるとは, $y=2x$となる$x\in{\mathbb{Z}}$が存在する」,「$y$が2の倍数であるとは, ある$x\in\mathbb{Z}$を用いて, $y=2x$と表せる」と読む。
なぜ集合を導入したのかというと, 定義域や値域が本来集合だからである。$x>0$と書いたら普通は「$x$は正の実数」と読むのに定義域のときだけ, 「$x$は正の実数全体を動く」は変ではないですか?後者の意味をもたせるなら, きちんと「$x$は
\begin{align*}
\{x\in\mathbb{R};x>0\}
\end{align*}
を動く」と書くべきでしょう。だから, 少なくともそれを意識してほしいのであえて集合を導入しましたが, なるべく不等式で表現しています。汚くなるとこだけ集合で書きました。量化記号は僕の怠慢です。
三角関数の最大・最小問題
三角関数の最大・最小問題のパターンは以下の通り。
定石
- 三角関数の合成
- 倍角の公式や半角の公式を使って多項式関数とみなす
- $t=a\sin{\theta}+b\cos{\theta}$と置いて、多項式関数とみなす($a=b=1$のとき誘導がないこともある)
- 積和の公式・和積の公式
- 曲線[とくに直線]と(単位)円との交点とみなして線形計画法
- 微分法(数学Ⅲ)
各々の簡単な例を見ていこう(微分法は略)
$\theta$は実数とする。以下の関数$f(\theta)$のとりうる値の範囲を求めよ。
(1) $f(\theta)=\sin{\theta}+\cos{\theta}\quad (0\leqq{\theta}\leqq{\pi})$
(2) $f(\theta)=\cos{2\theta}-4\cos{\theta}\quad (0\leqq{\theta}\leqq{\pi})$
(3) $f(\theta)=4\sqrt{2}\sin{\theta}\cos{\theta}-4\cos{\theta}-4\sin{\theta}\quad (0\leqq{\theta}\leqq{\pi})$
(4) $f(\theta)=\sin{\left(\theta+\dfrac{\pi}{6}\right)}\sin{\theta}$ ($\theta\in\mathbb{R}$)
(5) $f(\theta)=\dfrac{\sin{\theta}}{\cos{\theta}-2}\quad (0\leqq{\theta}\leqq{\pi})$
解答
三角関数の合成
(1)
$a, b$は$a^{2}+b^{2}\neq{0}$を満たす実数とする。ある$\alpha$を用いて, どんな実数$x$に対しても
\begin{align*}
a\sin{x}+b\cos{x}=\sqrt{a^{2}+b^{2}}\sin\left(x+\alpha\right)
\end{align*}
と表され, その$\alpha$とは
\begin{align*}
\sin{\alpha}=\dfrac{b}{\sqrt{a^{2}+b^{2}}}かつ, \cos{\alpha}=\dfrac{a}{\sqrt{a^{2}+b^{2}}}
\end{align*}
を満たす実数である。
\begin{align*}
f(\theta)=\sqrt{2}\sin{\left(\theta+\dfrac{\pi}{4}\right)}
\end{align*}
で、$\theta$は$0\leq{\theta}\leq{\pi}$の範囲を動くので, $-\dfrac{1}{\sqrt{2}}\leqq{\sin{\left(\theta+\dfrac{\pi}{4}\right)}}\leqq{1}.$よって$f(\theta)$のとりうる値の範囲は
$$
-1\leqq{f(\theta)}\leqq{\sqrt{2}}.
$$
倍角・半角の公式
(2)
$\theta$は任意の実数とする。
\begin{align*}
\sin{2\theta}=2\sin{\theta}\cos{\theta},
\end{align*}
\begin{align*}
\cos{2\theta}=2\cos^{2}{\theta}-1
\end{align*}
$\theta$は任意の実数とする。
\begin{align*}
\sin^{2}{\dfrac{\theta}{2}}=\dfrac{1-\cos{\theta}}{2},
\end{align*}
\begin{align*}
\cos^{2}{\dfrac{\theta}{2}}=\dfrac{1+\cos{\theta}}{2}
\end{align*}
\begin{align*}
f(\theta)&=\cos{2\theta}-4\cos{\theta}\\
&=2\cos^{2}{\theta}-1-4\cos{\theta}\\
&=2\left(\cos{\theta}-1\right)^{2}-3
\end{align*}
である。ここで, $\cos{\theta}$は, $0\leqq{\theta}\leqq{\pi}$の範囲で
\begin{align*}
-1\leqq{\cos{\theta}}\leqq{1}
\end{align*}
を動くので
\begin{align*}
g(t)=2(t-1)^{2}-3\, (-1\leqq{t}\leqq{1})
\end{align*}
の最小値が求める最小値で, この関数のグラフは, 軸が直線$t=1$で頂点が$(-1, -3)$の放物線の$-1\leqq{t}\leqq{1}$の部分である。よって, 値の範囲は$y\geqq{-3}$である。
対称式型
- $t=\sin{\theta}+\cos{\theta}\quad (0\leq{\theta}\leq{\pi})$とおく。
\begin{align*} \sin{\theta}\cos{\theta}&=\dfrac{1}{2}\{(\sin{\theta}+\cos{\theta})^{2}-(\sin^{2}{\theta}+\cos^{2}{\theta})\}\\ &=\dfrac{t^{2}-1}{2}. \end{align*}
以上から
\begin{align*}
4\sqrt{2}\sin{\theta}\cos{\theta}-4\cos{\theta}-4\sin{\theta}&=4\sqrt{2}\cdot\dfrac{t^{2}-1}{2}-4t\\
&=2\sqrt{2}\left(t-\dfrac{\sqrt{2}}{2}\right)^{2}-3\sqrt{2}
\end{align*}
である。
ただし(1)から$t$は
\begin{align*}
-1\leqq{t}\leqq{\sqrt{2}}.
\end{align*}
を動く。
よって,$y=2\sqrt{2}\left(t-\dfrac{\sqrt{2}}{2}\right)^{2}-3\sqrt{2}$のグラフは軸が直線$t=\dfrac{\sqrt{2}}{2}$で頂点が$\left(\dfrac{\sqrt{2}}{2}, -3\sqrt{2}\right)$の下に凸の放物線の$-1\leqq{x}\leqq{\sqrt{2}}$の部分である。
したがって、求める値の範囲は
$$
-3\sqrt{2}\leqq{f(\theta)}\leqq{}.
$$
和積・積和の公式
\begin{align*}
\sin{A}+\sin{B}=2\sin{\dfrac{A+B}{2}}\cos{\dfrac{A-B}{2}}
\end{align*}
\begin{align*}
\sin{A}-\sin{B}=-2\cos{\dfrac{A+B}{2}}\sin{\dfrac{A-B}{2}}
\end{align*}
\begin{align*}
\cos{A}+\cos{B}=2\cos{\dfrac{A+B}{2}}\cos{\dfrac{A-B}{2}}
\end{align*}
\begin{align*}
\cos{A}-\cos{B}=-2\sin{\dfrac{A+B}{2}}\sin{\dfrac{A-B}{2}}
\end{align*}
$\alpha, \beta$は任意の実数とする。
\begin{align*}
\cos{\alpha}\cos{\beta}=\dfrac{1}{2}(\cos{(\alpha+\beta)}+\cos{(\alpha-\beta)})
\end{align*}
\begin{align*}
\sin\alpha\sin\beta=-\dfrac{1}{2}(\cos{(\alpha+\beta)}-\cos{(\alpha-\beta)})
\end{align*}
\begin{align*}
\sin{\alpha}\cos{\beta}=\dfrac{1}{2}(\sin{(\alpha+\beta)}+\sin{(\alpha-\beta)})
\end{align*}
\begin{align*}
\cos{\alpha}\sin{\beta}=\dfrac{1}{2}(\sin{(\alpha+\beta)}-\sin{(\alpha-\beta)})
\end{align*}
(4)
\begin{align*}
f(\theta)=-\dfrac{1}{2}\left(\cos{\left(2\theta+\dfrac{\pi}{6}\right)}-\dfrac{\sqrt{3}}{2}\right).
\end{align*}
よって求める値の範囲は
$$
\dfrac{1}{4}(-2+\sqrt{3})\leqq{f(\theta)}\leqq{\dfrac{1}{4}(2+\sqrt{3})}
$$
線形計画法
(5)
\begin{align*}
k=\dfrac{\sin{\theta}}{\cos{\theta}-2}
\end{align*}
となる$\theta\in[0, \pi]$が存在することは
\begin{align*}
\sin{\theta}=k(\cos{\theta}-2)
\end{align*}
となる$\theta\in[0, \pi]$が存在することと同値で, これを言い換えると
\begin{align*}
直線y=k(x-2)が単位円と0\leqq{y}\leqq{1}の範囲で共有点をもつ
\end{align*}
ことである。それは, 以下の図から
$$
-\dfrac{1}{\sqrt{3}}\leqq{k}\leqq{0}.
$$
である。
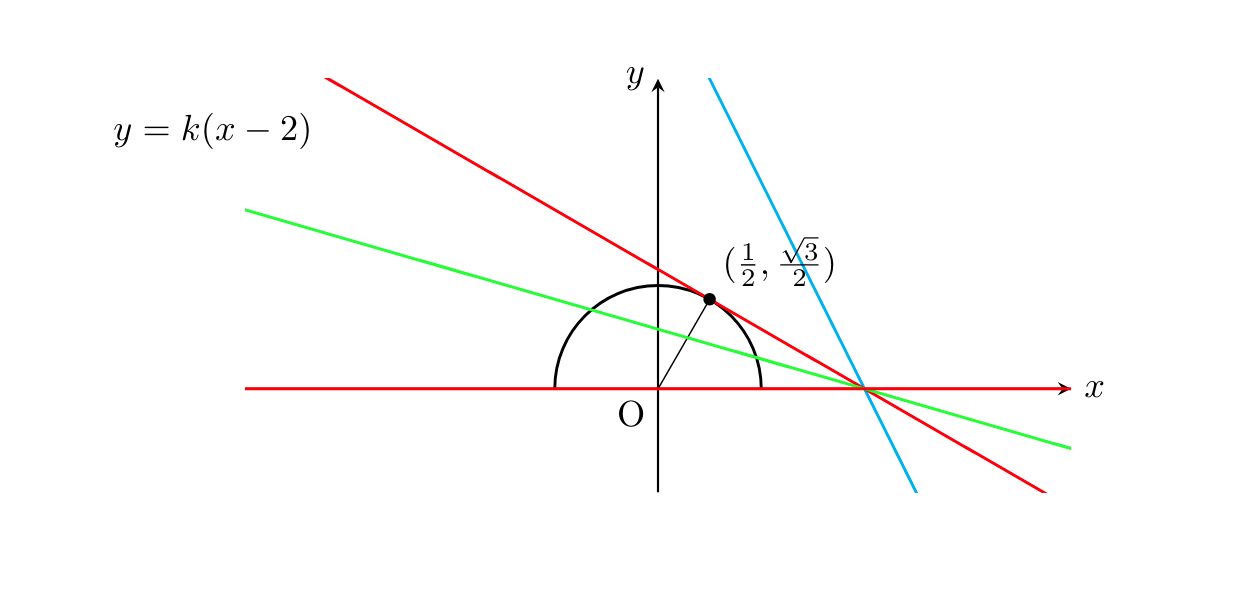 (5)の図
(5)の図
補足
(5)の$0\leq{k(0-2)}$は何をやっているかというと、直線と単位円(全体)が接するもうひとつを排除したいのだけど、そのときに$y=k(x-2)$が原点の上にあるので$0\leq{k(0-2)}$を利用して排除している。
応用的な例
$x$を実数とする。
$$
f(x)=\sin{3x}-9\cos{\left(x-\dfrac{\pi}{6}\right)}
$$
のとりうる値の範囲を求めよ。
方針
$t=\cos{\left(x-\dfrac{\pi}{6}\right)}$とおく。たまにこういう意地悪を見かける。これは、慶応のsfcの問題だった気がするやつを少し弄ったやつだが東北大でも同じような問題が出されている。また京大では、$t=\cos{2\theta}$とおくものがあった。
$\theta$は任意の実数とする。
\begin{align*}
\sin{3\theta}=3\sin{\theta}-4\sin^{3}{\theta},
\end{align*}
\begin{align*}
\cos{3\theta}=4\cos^{3}{\theta}-3cos{\theta}
\end{align*}
解答
$t=\cos{\left(x-\dfrac{\pi}{6}\right)}=$とおくと
\begin{align*}
\sin{3x}&=\cos{\left(\dfrac{\pi}{2}-3x\right)}\\
&=\cos{3\left(x-\dfrac{\pi}{6}\right)}\\
&=4\cos^{3}{\theta}-3\cos{\theta}\quad \left(\theta=x-\dfrac{\pi}{6}とおいた\right)\\
&=4t^{3}-3t
\end{align*}
よって
$$
f(x)=4t^{3}-12t\, (=g(t)とおく)
$$
\begin{align*}
\dfrac{d}{dt}g(t)=12(t+1)(t-1)
\end{align*}
であるから、$-1\leq{t}\leq{1}$の範囲で$g(t)$の増減表は以下のようになる。
| $t$ | -1 | $\cdots$ | 1 |
|---|---|---|---|
| $g^{\prime}(t)$ | $-$ | ||
| $g(t)$ | 2 | ↘︎︎ | -2 |
よって求める値の範囲は
$$
-2\leq{f(x)}\leq{2}.
$$
$\theta$が$-\dfrac{\pi}{2}\leqq{\theta}\leqq{\dfrac{\pi}{2}}$を動くときの
$f(\theta)=\dfrac{2}{3}\sin{3\theta}-\sin{\theta}-\sqrt{3}\cos{\theta}$
の最大値と最小値を求めよ。
$t=\sin{\theta}+\sqrt{3}\cos{\theta}\quad \left(-\dfrac{\pi}{2}\leqq{\theta}\leqq{\dfrac{\pi}{2}}\right)$とおくと
\begin{align*}
t=2\sin\left(\theta+\dfrac{\pi}{3}\right)
\end{align*}
なので$t$は
\begin{align*}
-1\leqq{t}\leqq{2}
\end{align*}
を動く。そして
\begin{align*}
\sin{3\theta}&=-\sin(3\theta+\pi)\\
&=-3\sin\left(\theta+\dfrac{\pi}{3}\right)+4\sin^{3}\left(\theta+\dfrac{\pi}{3}\right)\\
&=-\dfrac{3}{2}t+\dfrac{t^{3}}{2}
\end{align*}
なので
\begin{align*}
\dfrac{2}{3}\sin{3\theta}-\sin{\theta}-\sqrt{3}\cos{\theta}=\dfrac{1}{3}t^{3}-2t
\end{align*}
である。$g(t)=\dfrac{1}{3}t^{3}-2t -1\leqq{t}\leqq{2} $とおく。
\begin{align*}
g^{\prime}(t)&=t^{2}-2\\
&=(t-\sqrt{2})(t+\sqrt{2})
\end{align*}
なので, $g(t)$の増減表を書くと
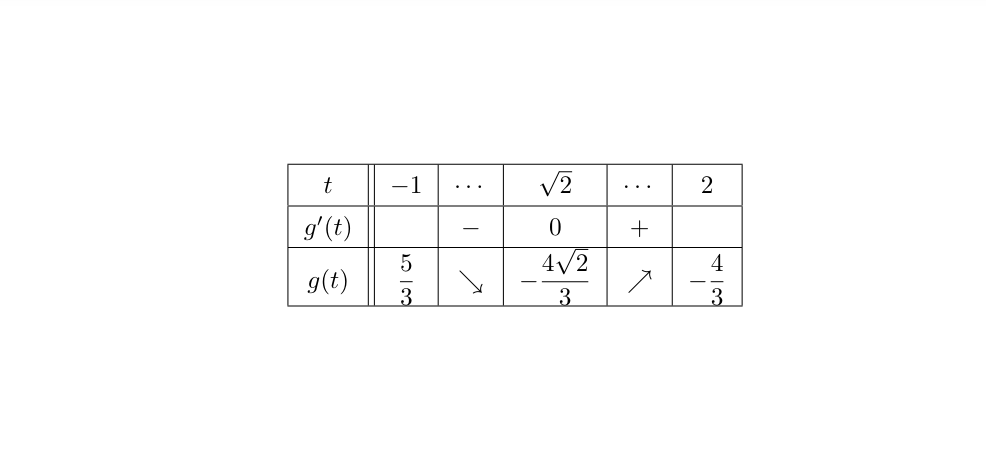 増減表
増減表
である。よって, 最大値は$\dfrac{5}{3}$で最小値は$-\dfrac{4\sqrt{2}}{3}$である。
$x$が$\sin{x}\neq{0}$かつ$\cos{x}\neq{0}$を満たす実数全体を動くとき
\begin{align*}
\left|\sin{x}+\cos{x}+\tan{x}+\dfrac{1}{\sin{x}}+\dfrac{1}{\cos{x}}+\dfrac{1}{\tan{x}}\right|
\end{align*}
の最小値を求めよ。
方針
$\sin{x}, \cos{x}$の「対称式」なので、$t=\sin{x}+\cos{x}$と置いて、$t$の式で表しましょう(もちろん$t$の値の範囲を求める必要がある)。そうすると$t$の有理式ができるので、相加平均と相乗平均の大小関係を使ってあげましょう。
解答
\begin{align*}
\sin{x}\cos{x}=0&\iff \sin{2x}=0\\
&\iff \exists n\in\mathbb{Z}, 2x=n\pi\\
&\iff \exists n\in\mathbb{Z}, x=\dfrac{n}{2}\pi
\end{align*}
である。$\sin{x}+\cos{x}=\sqrt{2}\sin{\left(x+\dfrac{1}{4}\pi\right)}$は, $x$が$\left\{x\in\mathbb{R};\, \exists n\in\mathbb{Z},x={\dfrac{n}{2}}\right\}^{c}$を満たして動くとき
\begin{align*}
[-\sqrt{2}, \sqrt{2}]-\{1, -1\}
\end{align*}
を動く。これを$D$とおく。そして, $\sin^{2}x+\cos^{2}=1$に注意すると
\begin{align*}
\sin{x}+\cos{x}+\tan{x}+\dfrac{1}{\sin{x}}+\dfrac{1}{\cos{x}}+\dfrac{1}{\tan{x}}&=(\sin{x}+\cos{x})+\dfrac{\sin{x}+\cos{x}+1}{\sin{x}\cos{x}}\\
&=(\sin{x}+\cos{x})+\dfrac{\sin{x}+\cos{x}+1}{\dfrac{1-(\sin{x}+\cos{x})^{2}}{2}}\\
&=(\sin{x}+\cos{x})+\dfrac{2(\sin{x}+\cos{x}+1)}{-1+(\sin{x}+\cos{x})^{2}}\\
&=(\sin{x}+\cos{x})+\dfrac{2}{(\sin{x}+\cos{x})-1}
\end{align*}
と変形できるから
\begin{align*}
\left|t+\dfrac{2}{t-1}\right|\quad (t\in{D})
\end{align*}
の最小値を求めればよい。
[1] $t\in(1, \sqrt{2}]$のとき
$t-1>0$なので
\begin{align*}
\left|t+\dfrac{2}{t-1}\right|&=t+\dfrac{2}{t-1}\\
&=t-1+\dfrac{2}{t-1}+1\\
&=2\sqrt{(t-1)\cdot\dfrac{2}{t-1}}+1\quad (\because\, 相加平均と相乗平均の大小関係)\\
&=2\sqrt{2}+1
\end{align*}
である。
[2] $t\in D-(1, \sqrt{2}]$のとき
$1-t>0$なので
\begin{align*}
\left|t+\dfrac{2}{t-1}\right|&=-\left(t+\dfrac{2}{t-1}\right)\\
&=1-t+\dfrac{2}{1-t}-1\\
&=2\sqrt{(1-t)\cdot\dfrac{2}{1-t}}-1\quad (\because\, 相加平均と相乗平均の大小関係)\\
&=2\sqrt{2}-1
\end{align*}
である。そして, 上の不等式は
\begin{align*}
1-t=\dfrac{2}{1-t},
\end{align*}
つまり
\begin{align*}
t=1-\sqrt{2}
\end{align*}
のときに成り立つ。
[1], [2]から求める最小値は,$2\sqrt{2}-1$である。
$\theta$を任意の実数とする。
\begin{align*}
t=\tan{\dfrac{\theta}{2}}
\end{align*}
とおくと
\begin{align*}
\sin{\theta}=\dfrac{2t}{1+t^{2}},
\end{align*}
\begin{align*}
\cos{\theta}=\dfrac{1-t^{2}}{1+t^{2}}
\end{align*}
である。
\begin{align*}
\sin{\theta}&=2\sin{\dfrac{\theta}{2}}\cos{\dfrac{\theta}{2}}\\
&=2\tan{\dfrac{\theta}{2}}\cos^{2}{\dfrac{\theta}{2}}\\
&=2\tan{\dfrac{\theta}{2}}\cdot\dfrac{1}{1+\tan^{2}{\dfrac{\theta}{2}}}\\
&=\dfrac{2t}{1+t^{2}},
\end{align*}
\begin{align*}
\cos{\theta}&=2\cos^{2}{\dfrac{\theta}{2}}-1\\
&=2\dfrac{1}{1+\tan^{2}{\dfrac{\theta}{2}}}-1\\
&=\dfrac{2}{1+t^{2}}-1\\
&=\dfrac{1-t^{2}}{1+t^{2}}
\end{align*}
である。
\begin{align*}
f(\theta)=\dfrac{1+\sin{\theta}}{3+\cos{\theta}} (-\pi<\theta<\pi)
\end{align*}
の最大値と最小値を求めよ。
解答
\begin{align*}
t=\tan{\dfrac{\theta}{2}}
\end{align*}
とおくと
\begin{align*}
f(\theta)&=\dfrac{1+\dfrac{2t}{1+t^{2}}}{3+\dfrac{1-t^{2}}{1+t^{2}}}\\
&=\dfrac{(t+1)^{2}}{2(t^{2}+2)}
\end{align*}
である。ここで, $t$は実数全体を動く。
\begin{align*}
\dfrac{1}{2}=\dfrac{(t+1)^{2}}{2(t^{2}+2)}
\end{align*}
のとき, $t=\dfrac{1}{2}$である。
$y\neq{\dfrac{1}{2}}$とする。
\begin{align*}
y=\dfrac{(t+1)^{2}}{2(t^{2}+2)}
\end{align*}
となる実数$t$が存在することは
\begin{align*}
(2y-1)t^{2}-2t+4y-1=0
\end{align*}
となる実数$t$が存在することと同値である。これは
\begin{align*}
(-1)^{2}-(2y-1)(4y-1)\geqq{0},
\end{align*}
つまり
\begin{align*}
0\leqq{y}<\dfrac{1}{2}, \dfrac{1}{2}< y\leqq{\dfrac{3}{4}}
\end{align*}
と同値である。以上から, 求める最大値は$\dfrac{3}{4}$で, 最小値は$0$である。
指数関数・対数関数の最大・最小
- $f(x)=4^{x+1}-2^{x+1}+1 (-1\leqq{x}\leqq{1})$の最大値と
最小値を求めよ。 - $f(x)=4^{x}+4^{-x}-2^{x+1}-2^{1-x} (x\in\mathbb{R})$の最小値を求めよ。
- $f(x)=(\log_{\frac{1}{3}}{x})^{2}-2\log_{\frac{1}{3}}{x} \left(\dfrac{1}{9}\leqq{x}\leqq{27}\right)$の値域を求めよ。
解答
$t=2^{x}(-1\leqq{x}\leqq{1})$とおくと
\begin{align*} 4^{x+1}-2^{x+1}+1&=4t^{2}-2t+1\\ &=4\left(t-\dfrac{1}{4}\right)^{2}+\dfrac{3}{4} \end{align*}
である。ただし, ここで$t$は
\begin{align*} \dfrac{1}{2}\leqq{t}\leqq{2} \end{align*}
を動く。$y=4\left(t-\dfrac{1}{4}\right)^{2}+\dfrac{3}{4}(\dfrac{1}{2}\leqq{t}\leqq{2})$のグラフは軸が直線$t=\dfrac{1}{4}$で頂点が$\left(\dfrac{1}{4}, \dfrac{3}{4}\right)$の下に凸の放物線$\dfrac{1}{2}\leqq{t}\leqq{2}$の部分である。よって, 最大値は$13$で最小値は1である。$t=2^{x}+2^{-x}(x\in\mathbb{R})$おくと
\begin{align*} 4^{x}+4^{-x}-2^{x+1}-2^{1-x}&=(2^{x}+2^{-x})^{2}-2-2(2^{x}+2^{-x})\\ &=t^{2}-2t-2\\ &=(t-1)^{2}-3 \end{align*}
である。ただし, $t$は
\begin{align*} t\geqq{2} \end{align*}
を動く(必要がある)。なぜなら, $2^{x}>0$だから相加平均と相乗平均の大小関係から
\begin{align*} t\geqq{2\sqrt{2^{x}\cdot2^{-x}}}=2 \end{align*}
だからである。よって, $y=(t-1)^{2}-3$は軸が直線$t=1$で頂点が$(1, -3)$の放物線の$t\geqq{2}$の部分である。よって, $f(x)\geqq{-2}$である。$f(x)=2$となるのは, $2=2^{x}+2^{-x}, $つまり$x=0$のときである。したがって, 最小値は$-2$である。$t=\log_{\frac{1}{3}}{x} \left(\dfrac{1}{9}\leqq{x}\leqq{27}\right)$とおくと, $t$の動く範囲は
\begin{align*} -3\leqq{t}\leqq{2} \end{align*}
で,
\begin{align*} (\log_{\frac{1}{3}}{x})^{2}-2\log_{\frac{1}{3}}{x}&=t^{2}-2t\\ &=(t-1)^{2}-1 \end{align*}
である。よって, $y=(t-1)^{2}-1 \left(\dfrac{1}{9}\leqq{x}\leqq{27}\right)$は軸が直線$t=1$で頂点が$(1, -1)$の下に凸な放物線の$\dfrac{1}{9}\leqq{x}\leqq{27}$の部分である。よって, 求める地域は
\begin{align*} -1\leqq{f(x)}\leqq{15} \end{align*}
である。
