レールの上の眠り姫問題

　実験の参加者である あなたは、実験の内容を全て説明され、眠りにつく。あなたが眠っている間に一度だけコインがトスされる。

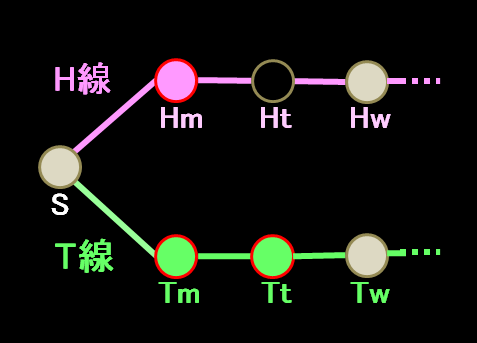路線図

• コインが表であった場合、あなたはS駅で、これからH線に入る列車に乗せられる。列車が最初の停車駅Hmに着いたら、あなたは起こされて、予め決められた ある質問（以降の「質問」も全く同じ内容である）をされたのち、ある薬（以降の「薬」も同じ薬である）を投与されて眠りにつく。その後は、列車がHw駅に着くまで起こされることはない。
• コインが裏であった場合、あなたはS駅で、これからT線に入る列車に乗せられる。列車が最初の停車駅Tmに着いたら、あなたは起こされて、質問をされたのち、薬を投与されて眠りにつく。次の停車駅Ttに着いたときも あなたは起こされて、質問をされたのち、薬を投与されて眠りにつく。その後は、列車がTw駅に着くまで起こされることはない。

　この実験で あなたに投与される薬は、誰かに起こされるまで絶対に目覚めないという睡眠導入薬で、直近の目覚めから投与時までの記憶を完全に消去する作用もある。よって、あなたが起こされ、質問を受ける際、以前に起こされたことがあるかどうかは分からない。加えて、あなたが乗せられている車両は中から外の様子を知る事が出来ないようになっている為、起こされた今、列車はどの駅で停車しているのか、あなたは決して知ることができない。
　コインが表／裏、どちらの場合でも、列車がHw／Tw駅に着けば、あなたは起こされ、質問は行われず、実験は終了する。
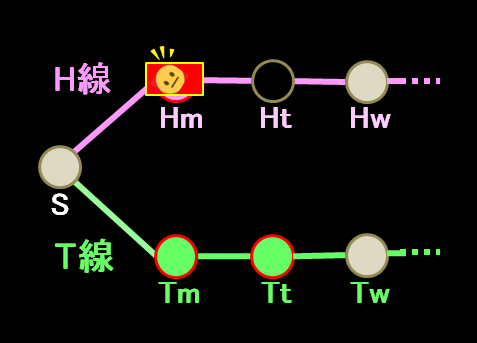
　さて、今あなたは起こされ、そして質問された ―「『今あなたはH線上にいる』ということに対する、今のあなたの信頼の度合いは（確率で表せば）いくらですか？」。あなたは何と答えるべきか？

　実験の参加者である あなたは、実験の内容を全て説明され、日曜日に眠りにつく。あなたが眠っている間に一度だけコインがトスされる。

• コインが表であった場合、あなたは月曜日に起こされ、予め決められたある質問（以降の「質問」も全く同じ内容である）をされたのち、ある薬（以降の「薬」も同じ薬である）を投与され眠りにつく。
• コインが裏であった場合、あなたは月曜日に起こされ、質問されたのち、薬を投与され眠りにつく。そして翌日の火曜日にも起こされ、質問されたのち、再び薬を投与されて眠りにつく。

　この実験であなたに投与される薬は、誰かに起こされるまで絶対に目覚めないという睡眠導入薬で、直近の目覚めから投与時までの記憶を完全に消去する作用もある。よって、あなたが起こされ、質問を受ける際、以前に起こされたことがあるかどうかは分からない。加えて、あなたは実験の間、起こされたその日が何曜日であるかを決して知ることができない環境に置かれているものとする。
　コインが表／裏、どちらの場合でも、水曜日になれば、あなたは起こされ、質問は行われず、実験は終了する。
　さて、今あなたは起こされ、そして質問された ―「『コイントスの結果が表だった』ということに対する、今のあなたの信頼の度合いは（確率で表せば）いくらですか？」。あなたは何と答えるべきか？

あなたが起こされた時、敢えて TmとTtは “互いに排反である”とみなすならば、
P(Hm) = 1/2、P(Tm) = P(Tt) = 1/4

　コイントスの結果が表／裏 どちらであるかに関わらず、月曜日には あなたは必ず起こされて質問されるので、もし あなたが起こされた時に、「今日は月曜日である」ことを知らされた とすると、明日の火曜日に起こされる確率は「コイントスの結果が裏であった確率」と同じ1/2だ。従って、「今」が、「明日も起こされる月曜日である」確率、つまり、「コイントスの結果が裏だった時の月曜日である」（Tm）確率は1/2、そして「明日は起こされない月曜日である」確率、つまり、「コイントスの結果が表だった時の月曜日である」（Hm）確率も1/2だ。
　しかし、遅読猫が主張しているように

　あなたが起こされた時、
　P(Hm) = 1/2、P(Tm) = P(Tt) = 1/4

だとしたら、「今日は月曜日である」という情報を与えられたなら、正規化の結果、

　P(Hm) = 2/3、P(Tm) = 1/3

となるはずである。だが これは先の論証の結果

　あなたが「今日は月曜日である」という情報を得た場合、
　P(Hm) = P(Tm) = 1/2

との間に齟齬を生じる。
　従って、遅読猫の主張する

　あなたが起こされた時、
　P(Hm) = 1/2、P(Tm) = P(Tt) = 1/4

は間違いであり、先の論証の結果との間に齟齬が生じない

　あなたが起こされた時、
　P(Hm) = P(Tm) = P(Tt) = 1/3

が正しい。