2024福島県高校入試の数学
今年もやります 問題はこちらから
が、正直大問1, 2は解答を見てくださいとしか言いようがないので飛ばします
大問3
(1)①
サイコロの目の出方は$6^2=36$通り
各点で一緒になることがちょうど一回ずつあるから
$\frac{6}{36}=\frac{1}{6}$
②
Aが頂角の二等辺三角形になればいい……だけではありません
Aの両脇の2点、こいつらも頂角になり得ます(正直解答見るまで気づかなかった)
それぞれ2通りずつ目の出方が存在するので
$\frac{8}{36}=\frac{2}{9}$
(2)①
n番目のタイルの総数は $n^2$ で表せる
したがって、$23^2=529$
②
n番目のタイルの総数とn-1番目のタイルの総数の差、すなわち、新たに敷くタイルの枚数を考えると、
$ n^2-(n-1)^2=2n-1 $
nは自然数であるから2n-1は奇数であり、したがって、新たに必要なタイルの枚数は奇数である
大問4
水を移す前の容器A, Bの水量をそれぞれx, y(mL)とすると、次の2つの式が成り立つ
$x+y=820$
$\frac{1}{4}x+\frac{1}{3}y=\frac{3}{4}x-60$
この連立方程式を解くと
$x=400(mL), y=420(mL)$
大問5
△AIEと△FIBの合同を示す方針でやります
$ 回転してできたから$
$BC=EC, AC=FC$
$また、AE=AC-EC, FB=FC-BC$
$ 以上より、AE=FB …①$
$ ∠AEI=∠FBI=90° …② $
$ ∠EAI=∠BFI=45° …③ $
$ ①, ②, ③より、一組の辺とその両端の角が$
$それぞれ等しいから $
$ △AIE≡△FIB $
$ よって、EI=BI $
大問6
(1)
$A(-2, 1)$より、$1 $
(2)
$B(6, 9) $であるから、傾きは
$\frac{6-(-2)}{9-1}=1 $
したがって、$l: y=x+k $とおくと、$(-2, 1)$を通るから
$1=-2+k $
$k=3 $
よって、$y=x+3 $
(3)
去年の共通テストみたいな問答が無くなりましたね、何だったんだあれ
$P(t, \frac{1}{4}t^2), Q(t, t+3), R(t, 0)$
$QP=t+3-\frac{1}{4}t^2, PR=\frac{1}{4}t^2$
$QP=PRより$
$t+3-\frac{1}{4}t^2=\frac{1}{4}t^2$
$t^2-2t-6=0$
$t=1±\sqrt{7}$
$0< t<6より、t=1+\sqrt{7}$
大問7
(1)
三平方の定理により
$EF^2=10^2-8^2 $
$EF=6$
(2)
$PR:AC=2:3 $
$PR:8=2:3$
$PR=\frac{16}{3}$
$また、PQ=AD=3\sqrt{2}$
$PQ⊥BCであるから、求める面積は$
$\frac{16}{3}×3\sqrt{2}=16\sqrt{2}$
(3)
まず$四角形ACSQ$を取り出すとこのようになります(手書きですみません)
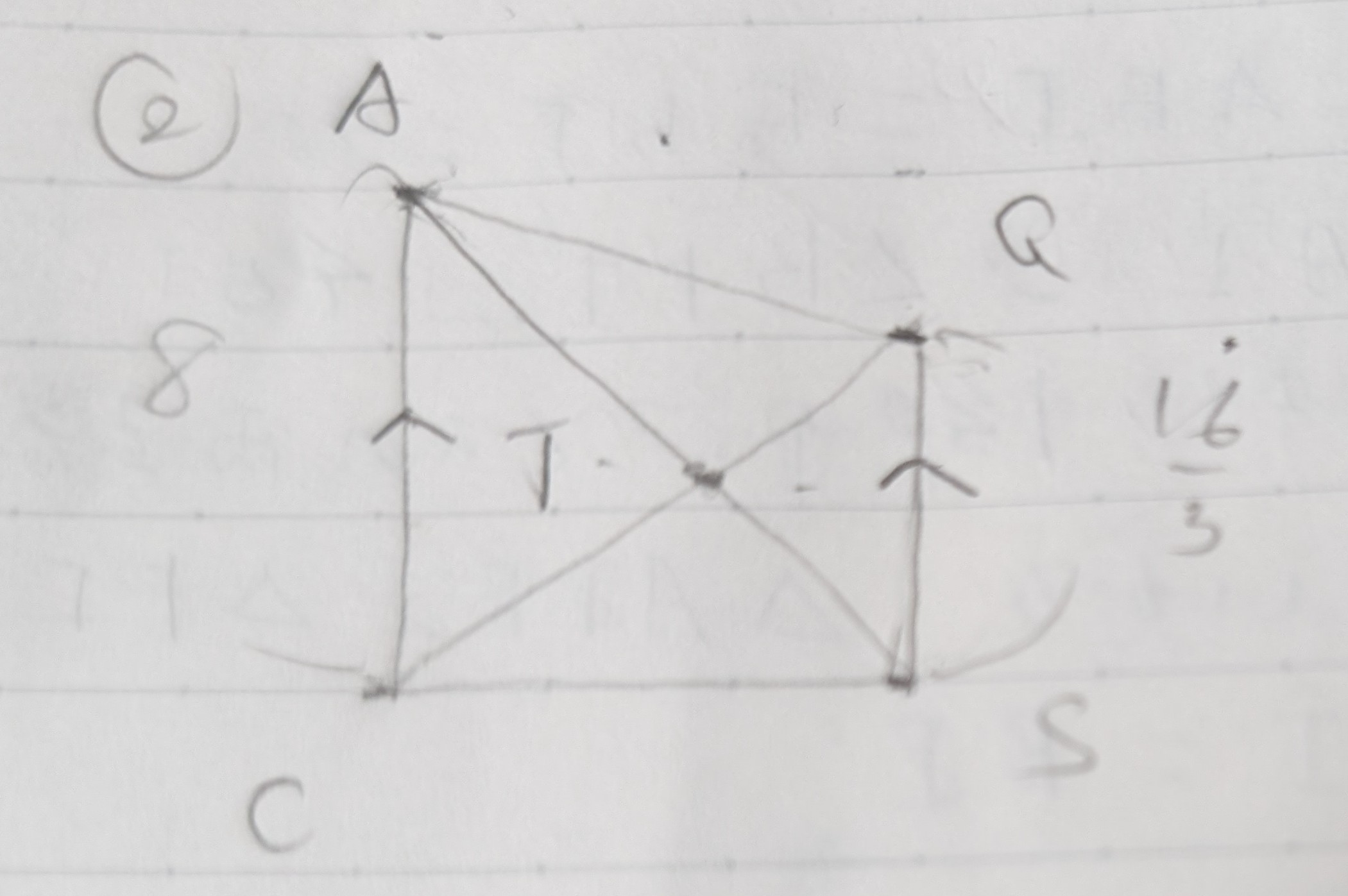 四角形ACSQ
四角形ACSQ
$AC//QS$なので$△ACT∽△SQT $です
相似比は$8:\frac{16}{3}=3:2$であるから、$AT:TS=3:2 $です
次に$△ASF$に着目しましょう
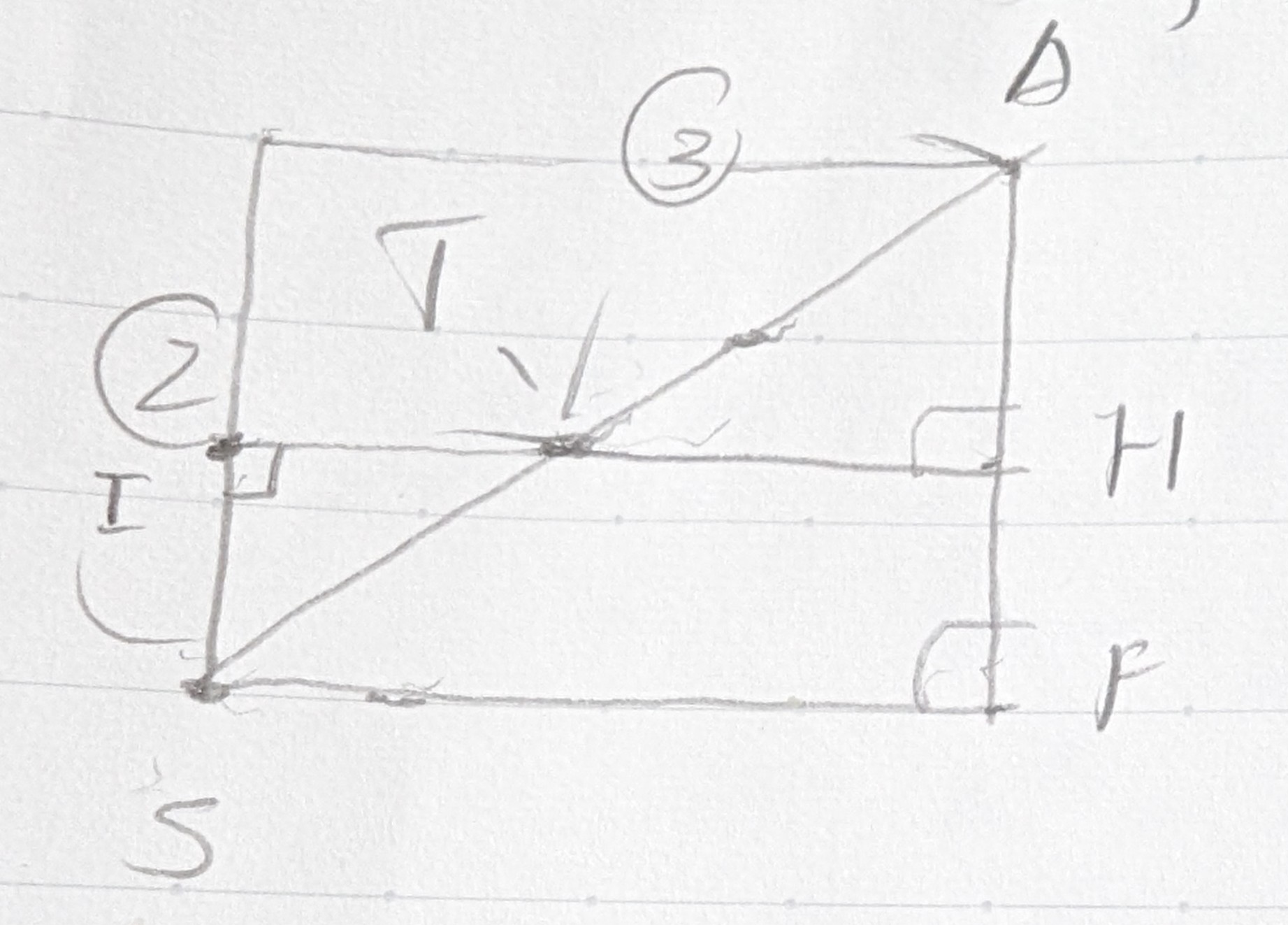 △ASF
△ASF
点Tから辺AFに引いた垂線と辺AFとの交点をHとすると、THの長さを出してSFから引く、もしくはSを通り線分SFに垂直な線と直線THとの交点をIとしてTIの長さを出す、のどちらかで四角錐の高さを出せます
今回は計算量が少ない後者でやりましょうかね
$SF=\frac{1}{3}EF=2$
$TI:2=2:5$
$TI=\frac{4}{5}$
したがって求める体積は
$16\sqrt{2}×\frac{4}{5}×\frac{1}{3}$
$=\frac{64\sqrt{2}}{15}$
感想
素直な問題だったと思います
最後を本番で解ききるのは少し難しいかな〜って思います
あと大問5は方針がすぐには立たなそうですかね