外接四角形の細胞分裂（未証明）
数学力のなさ
GeoGebraで遊んでいたら、次が成り立ちそうだとわかった。
四角形$ABCD$の辺$AB,BC,CD,DA$上に点$P,Q,R,S$を取り、図のように$4$つの四角形に分割すると、それらはすべて円に外接した。このとき、次が成り立つ。
- 四角形$ABCD$は円に外接する。
- 直線$AD,BC,PR$は$1$点で交わり（またはすべて平行）、直線$AB,CD,QS$も$1$点で交わる（またはすべて平行）。
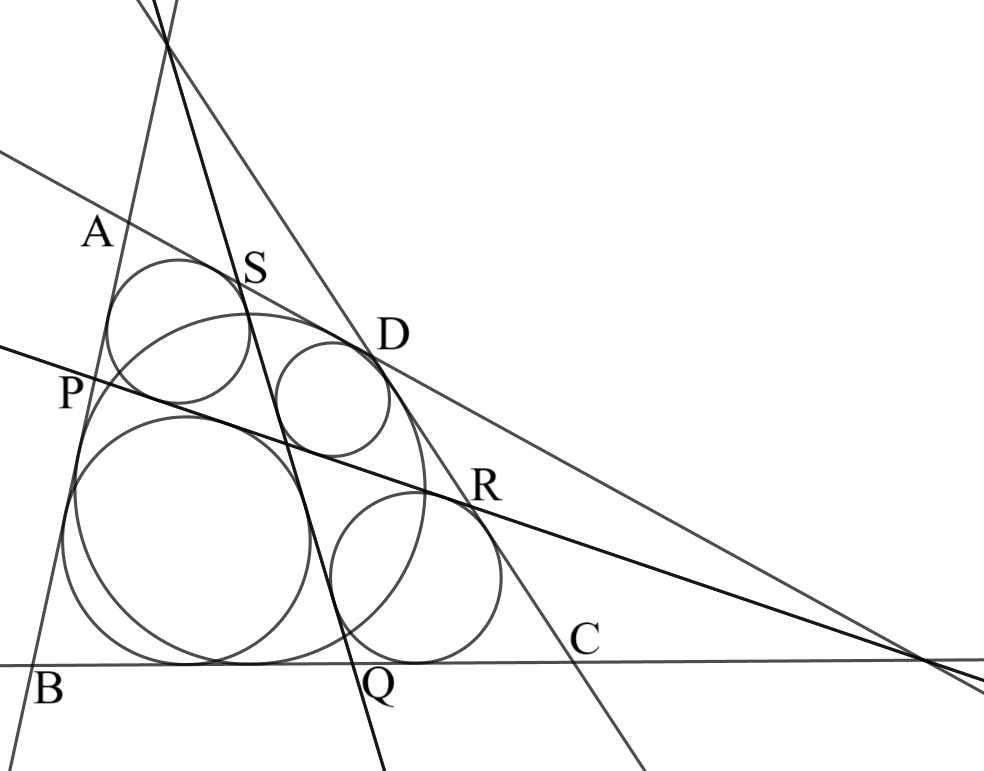ほーん、なんかすごい
証明の仕方はわからんけど、まあええわ。この図の発展形を考えてみよう。
四角形$ABCD$の辺$AB,BC,CD,DA$上に点$P_{1},P_{2},Q_{1},Q_{2},R_{1},R_{2},S_{1},S_{2}$を取り、図のように9つの四角形に分割すると、それらはすべて円に外接した。このとき、次が成り立つ。
- 四角形$ABCD$は円に外接する。
- 直線$AD,BC,P_{1}R_{1},P_{2}R_{2}$は$1$点で交わり（またはすべて平行）、直線$AB,CD,Q_{1}S_{1},Q_{2}S_{2}$は$1$点で交わる（またはすべて平行）。
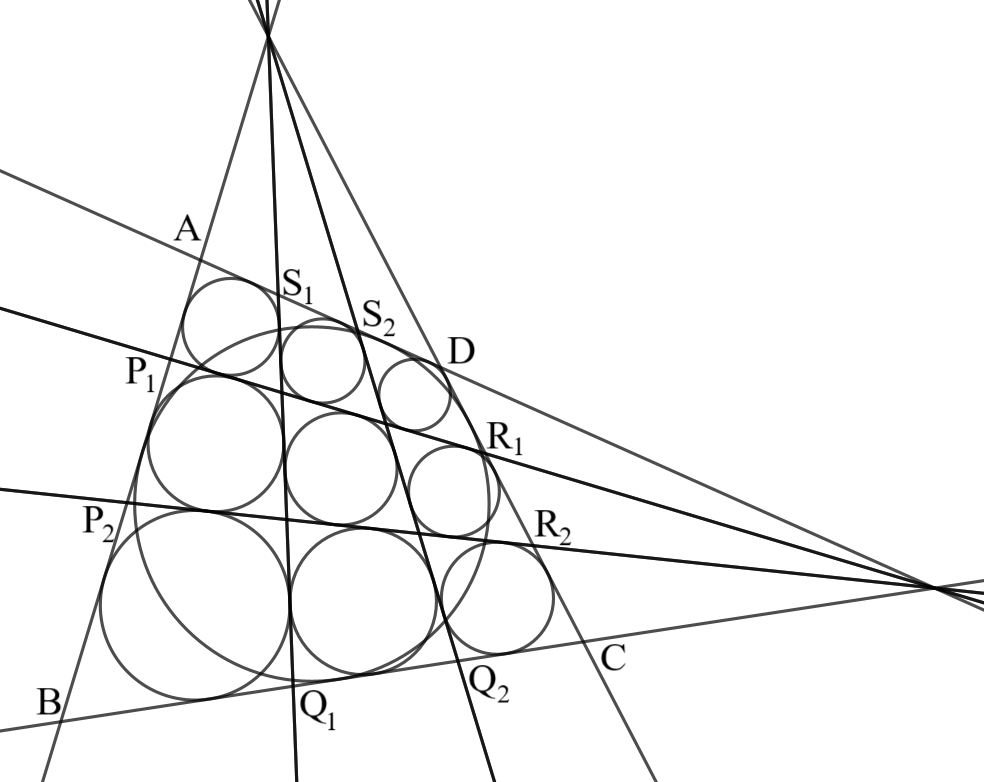外接四角形の細胞分裂
図を見る感じ、成り立ちそうである。$1$点に交わるのは、$2 \times 2$の方が証明できたら明らかにわかる。四角形$ABCD$が円に外接するのは、$2 \times 2$の方を証明できたとしても明らかにわかるとは言えないかも。どちらにしろ、証明の仕方わからんけど。
視点を変えて、最初に外接四角形を用意するなら、次の検討課題が考えられる。
円に外接する四角形$ABCD$の内部に点$X$を置き、図のように$X$を通る$2$つの直線によって四角形を$4$つに分割する。これら$4$つの四角形すべてが円に外接するとき、点$X$はどのような点か？また、点$X$は$1$つに定まるか。
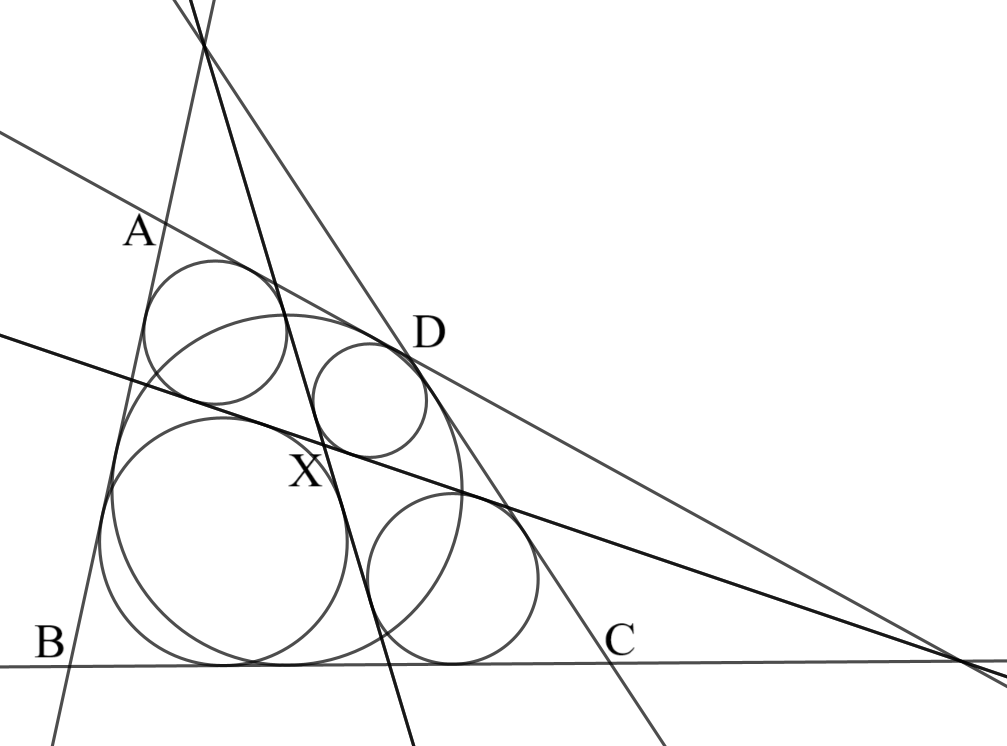これは左下の小四角形から作図しているよ
作図方法が知りたいよねという話。しかし、$X$がどのような特徴を持つ点かわからない。図をいじってみる限り、$1$つに定まりそうではある。
他にも課題は考えられる。
同様の図において、$4$つの円の中心を結んでできる四角形はどのような特徴を持つか？
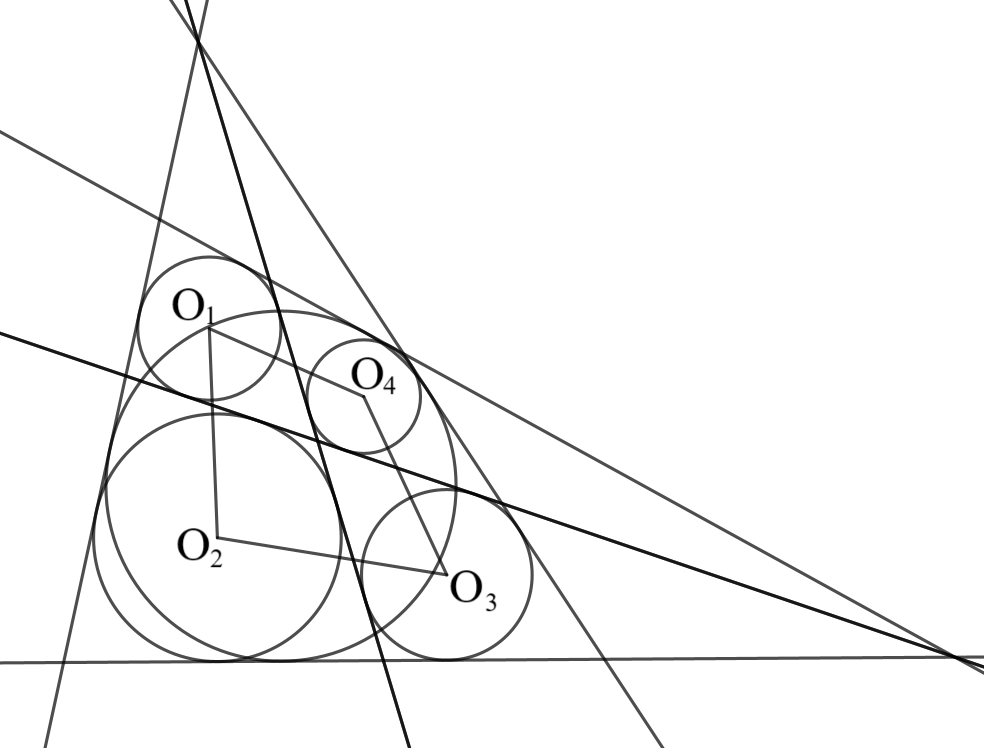
これ円に外接したりしないかな～と思ったけど、しませんでした。でも、何か面白い特徴があってほしい。
終
何も証明できてないのは残念であるが、見た目が楽しい。
