正n角形の面積公式

レベル低いけど正$n$角形の面積公式を出します.
おそらく多分高校までの知識でできます.

中心点から頂点までの距離をrとする.

周りの長さを求める

正$n$角形を合同な二等辺三角形に$n$等分した図形
この二等辺三角形の一辺の部分の$t$を求めるには余弦定理を利用します.

$ t^2 = r^2 + r^2 - 2r^2 \cos \theta $となり、計算すると
$ t = r \sqrt{2 -2 \cos \theta } $となる

二等辺三角形の高さを求める

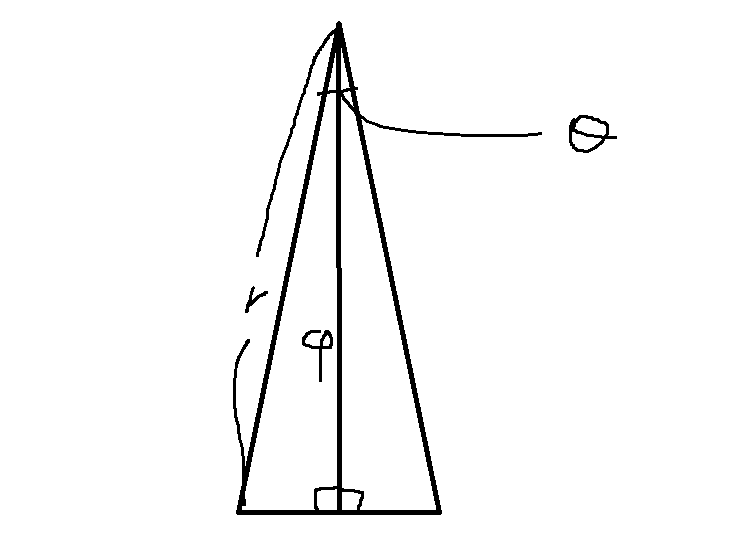二等辺三角形

二等辺三角形の高さ$ \varphi $は三平方の定理を使って計算できます.
$ \varphi^2 + ( \frac{t^2}{4} ) = r^2 $

$ \varphi^2 = r^2 - ( \frac{2r^2(1-\cos \theta )}{4} ) $となり

$ \varphi = \frac{r}{\sqrt{2}}\sqrt{ 1 + \cos \theta } $となります.

この二等辺三角形の面積$S$は$ \varphi \cdot t \cdot 0.5 $なので
$S= \frac{r}{\sqrt{2}}\sqrt{ 1 + \cos \theta } \cdot r \sqrt{2 - 2\cos \theta }\cdot\frac{1}{2} = r\sqrt{ 1 + \cos \theta } \cdot r \sqrt{1 - \cos \theta }\cdot\frac{1}{2}$となり、

$S = \frac{r^2}{2}\sqrt{1-\cos^2\theta}$このようになります.

$\sqrt{1-\cos^2\theta}=\sin\theta$なので

$S=\frac{r^2}{2}\sin\theta$となる

$\theta$は$2\pi$の$n$等分なので

$\theta = \frac{2\pi}{n}$

正$n$角形の面積は二等辺三角形の$n$倍なので、正$n$角形の面積は
$\frac{nr^2}{2}\sin\frac{2\pi}{n}$となる

正$n$角形の面積

正$n$角形の面積は中心点から頂点までの距離を$r$とすると
$\frac{nr^2}{2}\sin\frac{2\pi}{n}$である