(∞,1)圏のモデルについて

$(\infty,1)$圏のモデルについて勉強したことをまとめる.

もともとは自分のpdfに書いていた内容であるが, 構成の変更により消すことになったので, ここに残しておく.
ある記事のintroductionの章に書いていた内容なので, 詳しく解説しているわけではない.
詳しくは Higher Algebra cafe を参照してほしい.

$(\infty,1)$圏とは

$(\infty,1)$圏($(\infty,1)$-category)は任意の$n>1$に対して$n$射が可逆であるような弱$\infty$圏(weak $\infty$-category)である.
この$(\infty,1)$圏の情報をうまく組み込む方法(数学的対象)が多く考えられてきた.
実際, $(\infty,1)$圏のモデルとして単体的圏(simplicial category), Segal圏(Segal category), 完備Segal空間(complete Segal space), 擬圏(quasi-category), 相対圏(relative category)などがある.
(他にも, 位相的圏(topological category), dg圏(dg-category), $A_\infty$圏($A_\infty$-category), ホモトピカル圏(homotopical category)などがある.)
これらの圏はホモトピー論と(高次)圏論の両方の異なる動機から考えられた.
そして, BegnerやJoyal-Tierneyにより, これらの$(\infty,1)$圏のモデルが等価であることが示された.

Quillenによるモデル圏

まず, 「ホモトピー論」というと位相空間のホモトピー論が挙げられる.
ここでは, ホモトピー同値(homotopy equivalence)や弱ホモトピー同値(weak homotopy equivalence)である位相空間は同一視して扱いたい.
これを考えるために, CW複体やCW近似が定義され研究された.
この流れはホモロジー代数における複体のprojective resolutionなどにも見られる.

このような操作を一般的に行う枠組みとして, Quillenは1960年代にモデル圏(model category)を定義した.
モデル圏はweak equivalence, fibration, cofibrationの3つ組を用いて定義される.
モデル圏の局所化は集合論的な問題を避けることができるという利点がある.
また, モデル圏の同値としてQuillen同値(Quillen equivalence)がある.
このQuillen同値は圏とホモトピーの両方を保つような同値である.
よって, $(\infty,1)$圏のモデルの等価であるかは, 2つのモデル圏がQuillen同値であるかで判断することができる.

単体的圏

単体的圏は1980年代にDwyerとKanにより「ホモトピー論」を考えるために深く研究された.
weak equivalenceを持つ圏に対して, 単体的局所化(simplicial localization)やハンモック局所化(hammock localization)により単体的圏が得られる.
更に, 任意の単体的圏がDK同値(Dwyer-Kan equivalence)の違いを除いてこの方法により得られることが示された.
よって, 「ホモトピー論」がweak equivalenceを持つ圏であると思うと, 単体的圏はホモトピー論のモデルとして考えられる.

更に, 単体的圏の圏自体もDK同値をweak equivalenceとして持つ圏となる.
つまり, 単体的圏の圏も「ホモトピー論」を表すと考えられる.
よって, 単体的圏の圏は「ホモトピー論のホモトピー論」のモデルと思える.
この単体的圏の圏上にはBergnerモデル構造が存在する.
しかし, このモデル構造は単体的モデル圏(simplicial model category)でなかったり, weak equivalenceの判定が難しかったりなど扱いづらい.
そのため, 単体的圏の圏上のBergnerモデル構造とQuillen同値である, より良い構造を持つモデル圏が考えられるようになった.

Segal圏

$(\infty,1)$圏の他のモデルとしてSegal圏がある.
Segal圏は1990年代にDywer, Kan, Smithにより「up to homotopyで合成が定義されるような単体的圏」として定義された.
HirschowitzとSimpsonは圏論的な視点からSegal圏を調べ, PellissierはSegal前圏上のモデル構造を与えた.

完備Segal空間

完備Segal空間は2000年代始めにRezkにより「ホモトピー論のホモトピー論」のモデルとして考案された.
完備Segal空間はいくつかの条件を満たす単体的空間である.
単体的空間の圏上のReedyモデル構造におけるweak equivalenceはlevelwiseに定義されるために扱いやすい.
Reedyモデル構造のBousfield局所化(Bousfield localization)で得られるRezkモデル構造はCartesianモデル圏であるなど, 単体的圏の圏上のBergnerモデル構造より良い性質を多く持つ.

擬圏

擬圏は1970年代にBoardmanとVogtにより定義され, JoyalやLurieなどにより深く調べられた.
Segal圏や完備Segal空間は単体的空間上で定義されるが, 擬圏は単体的集合上で定義される.
このため, 擬圏は他のモデルよりも扱いやすいという利点がある.
Quillenにより単体的集合の圏上にQuillenモデル構造が定義され, JoyalによりJoyalモデル構造が定義された.
Quillenモデル構造は位相空間の圏上のKan-Quillenモデル構造とQuillen同値であるため, $(\infty,0)$圏のモデルと見れる.
一方, Joyalモデル構造は単体的圏の圏上のBergnerモデル構造とQuillen同値であるため, $(\infty,1)$圏のモデルと思える.

相対圏

BarwickとKanは2010年代始めにweak equivalenceを持つ圏を相対圏として定義し, 「ホモトピー論のホモトピー論」のモデルの枠組みとして考えた.
彼らは単体的空間の圏上のRezkモデル構造とQuillen同値になるように, 相対圏の圏上のBarwickモデル構造を与えた.

まとめ

実際, 次のようなQuillen同値の列が存在する.

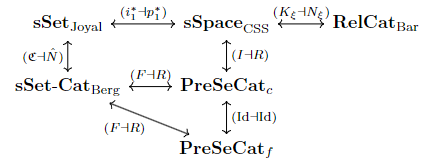Quillen同値の列