円を使って1/(1×2) + 1/(2×3) + 1/(3×4) ・・・ = 1を示そう!
はじめに
はじめまして^^
?! m と申します m(_ _)m
今回は円を使って$\frac{1}{1×2} + \frac{1}{2×3} + \frac{1}{3×4} + \cdots = 1$を示そうと思います。
その前に前提知識を3つ得ましょう。
一つ目の前提知識

線上に二円、円$A$、円$B$があり、それらは互いに接している。
円$A$の直径を$p$、円$B$の直径を$q$とすると ($p \geq q$)
接点$C$から接点$D$までの長さは$\sqrt{pq}$
点$A$と点$B$から直線に対して垂線を下ろし、交点をそれぞれ点$C$、点$D$とする。
点$B$から線分$AC$に垂線を下ろし、交点を点$E$とする。
点$A$と点$B$を結ぶ。
すると、直角三角形$AEB$ができる。
直角三角形なので、$AE^2 + EB^2 = AB^2$が成り立つ。
$AE = \frac{p}{2} - \frac{q}{2}$ $AB = \frac{p}{2} + \frac{q}{2}$
$(\frac{p}{2} - \frac{q}{2})^2 + EB^2 = (\frac{p}{2} + \frac{q}{2})^2$
$(\frac{p^2}{4} - \frac{pq}{2} + \frac{q^2}{4}) + EB^2 = (\frac{p^2}{4} + \frac{pq}{2} + \frac{q^2}{4})$
$EB^2 = pq$
$EB = \sqrt{pq}$
$EB = CD$
$CD = \sqrt{pq}$
二つ目の前提知識

線上に二円、円$A$、円$B$があり、それらは互いに接している。
さらにその二円の間にあり、二円と直線に接する円$C$があるとする。
円$A$の直径を$p$、円$B$の直径を$q$、円$C$の直径を$r$とすると、($p \geq q \gt r$)
$r = \frac{pq}{(\sqrt{p} + \sqrt{q})^2}$
点$A$、点$B$、点$C$から直線に対して垂線を下ろし、交点をそれぞれ点$D$、点$E$、点$F$とする。
すると、$DF = DE + EF$となる。
線上二円定理より、$DF = \sqrt{pq}$ $DE = \sqrt{pr}$ $EF = \sqrt{qr}$
代入すると、
$\sqrt{pq} = \sqrt{pr} + \sqrt{qr}$
$\sqrt{pq} = \sqrt{r}(\sqrt{p} + \sqrt{q})$
$\frac{\sqrt{pq}}{\sqrt{p} + \sqrt{q}} = \sqrt{r}$
$\frac{pq}{(\sqrt{p} + \sqrt{q})^2} = r$
三つ目の前提知識
三つ目の前提知識は、
線上に二円、円$A$、円$B$があり、それらは互いに接している。
さらにその二円の間にあり、二円と直線に接する円$C$が存在することを証明します。
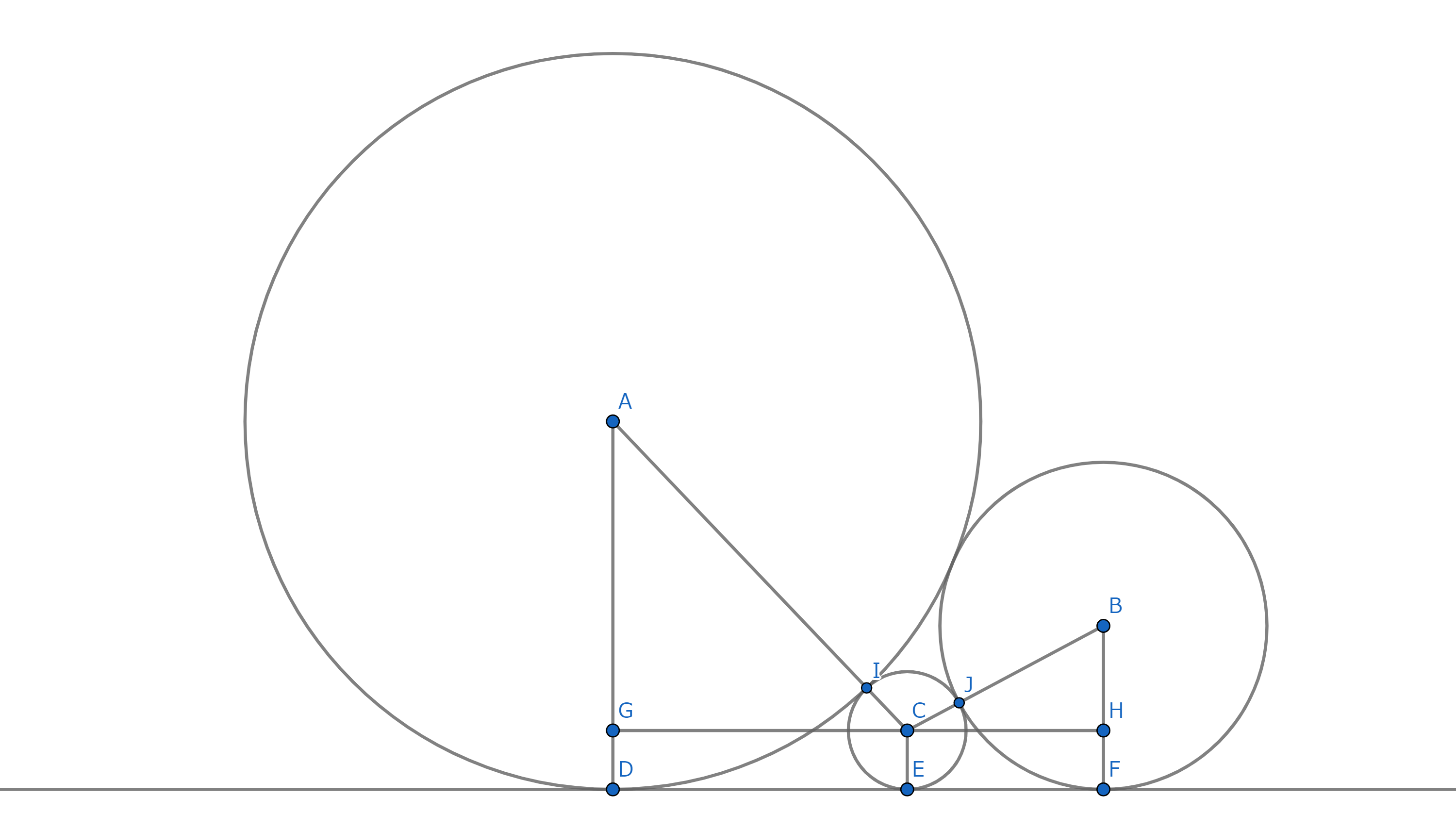

円$A$の直径を$p$、円$B$の直径を$q$、円$C$の直径を$r$とする。
点$A$と点$B$から直線に対して垂線を下ろし、交点をそれぞれ点$D$、点$F$とする。
仮に円$A$と円$B$の間に円$C$があるとしたら、その直径は$r = \frac{pq}{(\sqrt{p} + \sqrt{q})^2}$である。
ここで、図$4$のような直角三角形$MKL$を考える。
$KL = \frac{p}{2} - \frac{r}{2}$ $ML = \frac{p}{2} + \frac{r}{2}$である。
直角三角形なので$MK^2 + KL^2 = ML^2$が成り立つ。
代入すると、
$MK^2 + (\frac{p}{2} - \frac{q}{2})^2 = (\frac{p}{2} + \frac{q}{2})^2$
$MK^2 + (\frac{p^2}{4} - \frac{pq}{2} + \frac{q^2}{4}) = (\frac{p^2}{4} + \frac{pq}{2} + \frac{q^2}{4})$
$MK^2 = pq$
$MK = \sqrt{pq}$
点$D$から$MK$と同じ長さになるような点$E$を打つ
点$E$から上の方向に$\frac{r}{2}$分の垂線を下ろし、先端の点を$C$とする。
点$C$から線分$AD$、線分$BF$に垂線を下ろし、交点をそれぞれ点$G$、点$H$とする。
点$C$を点$A$、点$B$と結ぶ
すると直角三角形$AGC$、$BHC$ができる。
線分$AC$と円$A$の交点を点$I$、線分$BC$と円$B$の交点を$J$とする。
直角三角形$AGC$について考える。
直角三角形なので$AG^2 + GC^2 = AC^2$が成り立つ。
$AG = \sqrt{pq}$ $AG = {\frac{p}{2} - \frac{r}{2}}$
代入すると、
$(\frac{p}{2} - \frac{q}{2})^2 + (\sqrt{pq})^2 = AC^2$
$(\frac{p^2}{4} - \frac{pq}{2} + \frac{q^2}{4}) + pq = AC^2$
$(\frac{p}{2} + \frac{r}{2})^2 = AC^2$
$\frac{p}{2} + \frac{r}{2} = AC$
$AC = AI + IC$
$\frac{p}{2} + \frac{r}{2} = \frac{p}{2} + IC$
$\frac{r}{2} = IC$
よって、$EC = IC$
次に直角三角形$BHC$について考える。
直角三角形なので、$BH^2 + HC^2 = BC^2$
$BH = \frac{q}{2} - \frac{r}{2}$
$HC$の長さについて考える。
$HC = GH - GC$
$= \sqrt{pq} - \sqrt{pr}$
$= \sqrt{p}(\sqrt{q} - \sqrt{r})$
$= \sqrt{p}(\sqrt{q} - \frac{\sqrt{pq}}{\sqrt{p} + \sqrt{q}})$]
$= \sqrt{p}(\frac{q}{\sqrt{p} + \sqrt{q}})$
$= \sqrt{q}(\frac{\sqrt{pq}}{\sqrt{p} + \sqrt{q}})$
$= \sqrt{qr}$
代入すると、
$(\frac{q}{2} - \frac{r}{2})^2 + (\sqrt{qr})^2 = BC^2$
$(\frac{q^2}{4} - \frac{qr}{2} + \frac{r^2}{4}) + qr = BC^2$
$(\frac{q}{2} + \frac{r}{2})^2 = BC^2$
$\frac{q}{2} + \frac{r}{2} = BC$
$BC = BJ + JC$
$\frac{q}{2} + \frac{r}{2} = \frac{q}{2} + JC$
$\frac{r}{2} = JC$
よって、$EC = IC = JC$
線分$EC$は直線に接しており、線分$IC$は円$A$に接しており、線分$JC$は円$B$に接している。
つまり、三つの線分を半径とした円を作図する事ができ、それらは二円と直線に接しており、存在することの証明となった。
本題

直径が$1$の円$A$と円$B$がある。
円$A$と円$B$の間に円$C$がある。
接点$H$から接点$I$までの距離は線上二円定理より$1$である。
さらに円$A$と円$C$の間に円$D$、円$A$と円$D$の間に円$F$、円$A$と円$F$の間に$\cdots$という具合で無限に円が続いていく。(円$B$側も同様)
ただし、接点$H$、接点$I$を超えることはない
円$C$の直径を求める。
線上三円定理より、$\frac{1}{(\sqrt{1} + \sqrt{1})^2} = \frac{1}{4}$
円$D$の直径を求める。
$\frac{\frac{1}{4}}{(\sqrt{1} + \sqrt{\frac{1}{4}})^2} = \frac{1}{9}$
円$F$の直径を求める。
$\frac{\frac{1}{9}}{(\sqrt{1} + \sqrt{\frac{1}{9}})^2} = \frac{1}{16}$
その後も円の直径を求めていくと、$\frac{1}{25}$、$\frac{1}{36}$、$\frac{1}{49}$、$\cdots$と続いていく。
これらの数字には規則性があり、全て平方数であり、かつ$1^2、2^2、3^2、4^2 \cdots$と順番どおりである。
なぜ平方数かつ順番通りなのか?
直径が$1$の円と直径が$\frac{1}{n^2}$の円を想像する。(それらは線上にあり、互いに接している。)
二円の間にある円の直径を求める。
$\frac{\frac{1}{n^2}}{(\sqrt{1} + \sqrt{\frac{1}{n^2}})^2} = \frac{1}{(n + 1)^2}$
$n + 1 = k$とすると
$\frac{\frac{1}{k^2}}{(\sqrt{1} + \sqrt{\frac{1}{k^2}})^2} = \frac{1}{(k + 1)^2} = \frac{1}{(n + 2)^2}$
その後も計算していくと、$\frac{1}{(n + 3)^2}$、$\frac{1}{(n + 4)^2}$、$\frac{1}{(n + 5)^2}$、$\cdots$、と続いていく。
$n$に$1$を代入すると、$\frac{1}{1^2}、\frac{1}{2^2}、\frac{1}{3^2}、\cdots$と平方数かつ順番通りに続いていく。
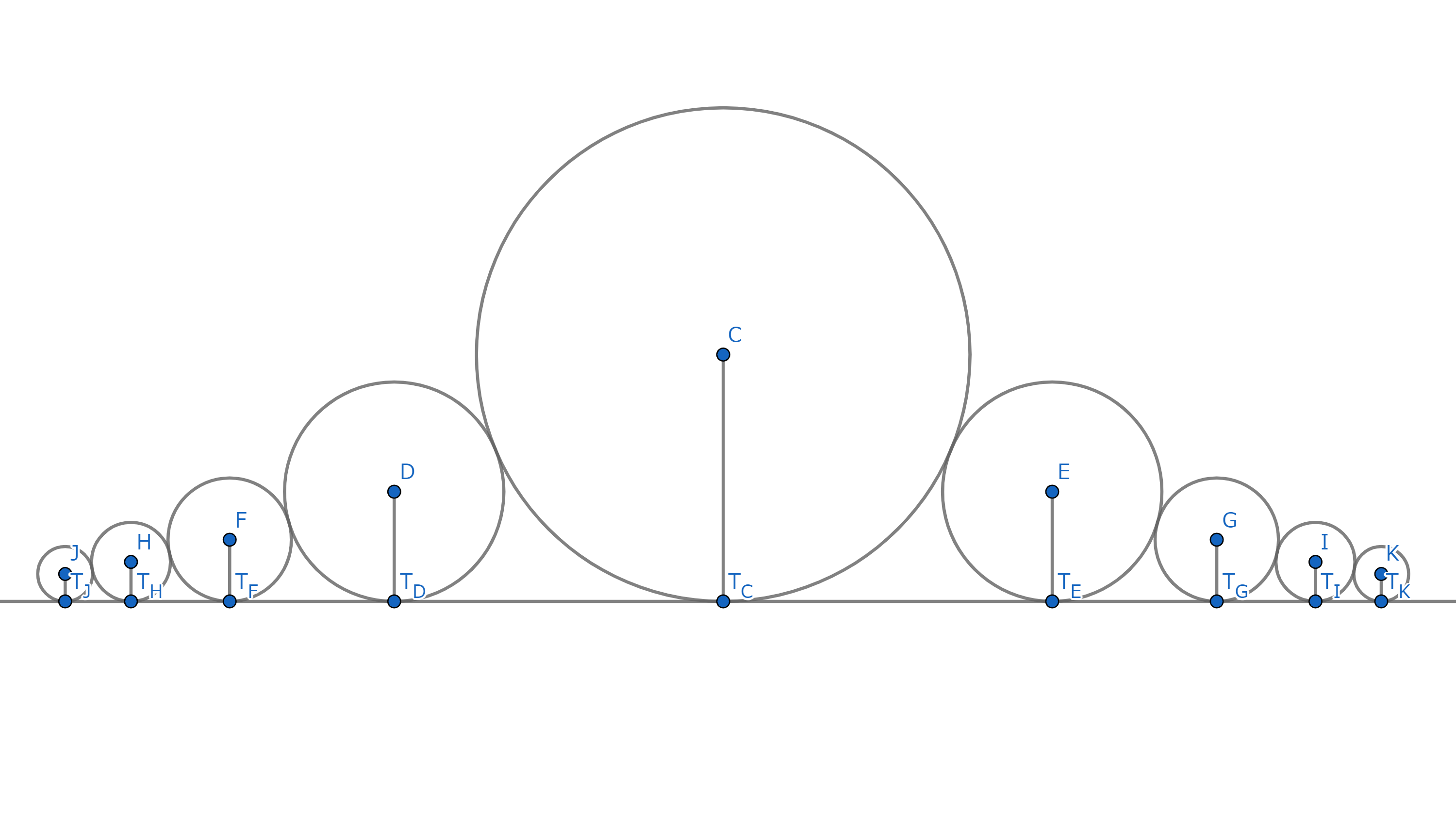
図$6$は図$5$の無限に連なる円を拡大した図である。
接点$\mathrm{T}_C$から接点$\mathrm{T}_D$までの距離を求める。
線上二円定理より$\sqrt{\frac{1}{4} × \frac{1}{9}} = \frac{1}{6}$
接点$\mathrm{T}_D$から接点$\mathrm{T}_F$までの距離を求める。
$\sqrt{\frac{1}{9} × \frac{1}{16}} = \frac{1}{12}$
接点$\mathrm{T}_F$から接点$\mathrm{T}_H$までの距離を求める。
$\sqrt{\frac{1}{16} × \frac{1}{25}} = \frac{1}{20}$
接点$\mathrm{T}_H$から接点$\mathrm{T}_J$までの距離を求める。
$\sqrt{\frac{1}{25} × \frac{1}{36}} = \frac{1}{30}$
その後も接点と接点との距離を求めていくと、$\frac{1}{42}$、$\frac{1}{56}$、$\frac{1}{72}$、$\cdots$と続いていく。
接点$\mathrm{T}_C$から接点$H$までの距離は$\frac{1}{2}$なので、
$\frac{1}{6} + \frac{1}{12} + \frac{1}{20} + \frac{1}{30} + \frac{1}{42} + \frac{1}{56} \cdots = \frac{1}{2}$
円$B$側にも同じ距離があるため、$2$をかける
$\frac{1}{3} + \frac{1}{6} + \frac{1}{10} + \frac{1}{15} + \frac{1}{21} + \frac{1}{28} \cdots = 1$
$\frac{1}{3}(\frac{1}{1} + \frac{1}{2}) + \frac{1}{5}(\frac{1}{2} + \frac{1}{3}) + \frac{1}{7}(\frac{1}{3} + \frac{1}{4}) + \cdots = 1$
$\frac{1}{3}(\frac{3}{1 × 2}) + \frac{1}{5}(\frac{5}{2 × 3}) + \frac{1}{7}(\frac{7}{3 × 4}) \cdots = 1$
$\frac{1}{1 × 2} + \frac{1}{2 × 3} + \frac{1}{3 × 4} \cdots = 1$
よって、タイトルの式が示された。
なぜ$\frac{1}{n(n+1)}$になるのか?
直径が$\frac{1}{(2n)^2}$の円、直径が$\frac{1}{(2n+1)^2}$の円、直径が$\frac{1}{(2n+2)^2}$の円を想像する。
線上二円定理より、$\sqrt{\frac{1}{(2n)^2} × \frac{1}{(2n + 1)^2}} + \sqrt{\frac{1}{(2n+1)^2} × \frac{1}{(2n + 2)^2}}$
$= \frac{1}{2n+1}(\frac{1}{2n} + \frac{1}{2n + 2})$
$2$をかける。
$= \frac{1}{2n+1}(\frac{1}{n} + \frac{1}{n + 1})$
$= \frac{1}{2n+1}(\frac{2n+1}{n(n+1)})$
$= \frac{1}{n(n + 1)}$
おわりに
これは私が中学時代に思いついたものです。
歴史の教科書を見ていた時に和算のコラムがありまして、そこに次のような問題がありました。
「直径が36寸の大円と9寸の中円の間にある小円の直径を求めよ」
これを解いた後思いました。
「大円の直径を$p$、中円の直径を$q$として小円の直径$r$を表してみるか」
そして、線上二円定理と線上三円定理を思いつきました。
その後なぜだかわかりませんが図5が思いついて、タイトルの式が導けたわけです。
、、、
ちなみに線上二円定理という名前は中村信弥氏の「和算の図形公式」から借りました。
検索すれば出てくるはずです。
いろんな公式が載ってるので楽しめますよ。(もちろん証明もあり)
、、、
最後まで読んでいただきありがとうございました!!!m(_ _)m
(間違っている個所があったら指摘していただけると幸いです。高評価してくれたら嬉しいです!)