高校数学解説

文献あり

超幾何級数かっこいい！やってみたい！(漸化式と超幾何級数)

漸化式,超幾何級数

導入

私と関わりのあるみゆ様がこんなツイートをしました。
かなり面白い式なので、証明してみました。

超幾何級数

ところで、

$ \F43{a,b,c,d}{e,f,g}{x} $

こういう式、かっこいいですよね？
やってみたいですよね？

では、この問題を使って実際にやってみましょう！

問題

方程式$ x^2 + bx + c = 0 $の$ 2 $解を$ x, \bar{x} $とする。このとき、
$ \displaystyle x^n + \bar{x}^n = (-1)^n n \sum_{k=0}^{\lfloor \frac{n}{2} \rfloor} \frac{(-1)^k (n - k - 1)!}{k! (n - 2k)!} b^{n - 2k} c^k $
であることを示せ。

なんともいかつい式ですね。実はこれは超幾何級数の一種です。記事の最後にはかっこいい書き方もあります。

証明

準備

$ A_n = x^n + \bar{x}^n, a_n = \frac{b_n}{(-1)^n} $とします。このとき、

\begin{align*} & A_{n+1} \\ =& x^{n+1} + \bar{x}^{n+1} \\ =& (x^n + \bar{x}^n)(x + \bar{x}) - x\bar{x}(x^{n-1} + \bar{x}^{n-1}) \\ =& -b A_{n} - c A_{n-1} \end{align*}

\begin{align*} A_{n+1} &= -b A_{n} - c A_{n-1} \\ \frac{A_{n+1}}{(-1)^{n+1}} &= \frac{-b A_{n}}{(-1)^{n+1}} - \frac{c A_{n-1}}{(-1)^{n+1}} \\ \frac{A_{n+1}}{(-1)^{n+1}} &= \frac{b A_{n}}{(-1)^n} - \frac{c A_{n-1}}{(-1)^{n-1}} \\ a_{n+1} &= b a_n - c a_{n-1} \\ a_{n+1} - b a_n + c a_{n-1} &= 0 \end{align*}

が成り立ちます。

割り算

ここで、多項式の割り算について考えます。特に、商が昇べきの順に並ぶものを考えます。

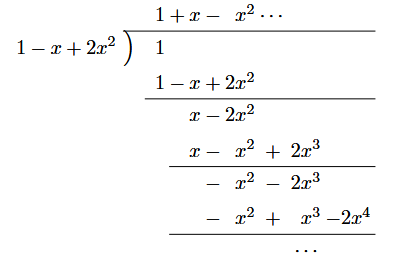MathlogのTeXには`cline`がない MathlogのTeXにはclineがない

このように、割り算は無限に続くことがあります。

この割り算の性質を1つ示します。

$ d $次多項式を$ 1 + px + qx^2 (p, q \in \mathbb{R}) $で商が昇べきの順になるよう割り、その商の$ m $次の項を$ r_n $とする。このとき、$ n + 2 > d $であれば次が成り立つ:
$ r_{n+2} + pr_{n+1} + qr_{n} = 0 $

有限次の多項式$ (1 + px + qx^2)(r_0 + r_1 x + \cdots + r_{n+3} x^{n+3}) $の$ n+2 $次の係数が$ r_{n+2} + pr_{n+1} + qr_{n} $であることから従う。

かっこいいやつ

ここからの議論を進めるために、かっこいい記号を導入します。

ポッホハマー記号

実数$ a $と$ 0 $以上の整数$ n $に対し、
$ (a)_n = a (a + 1) \cdots (a + n - 1) $
と定義する。
ただし、$ n = 0 $のときは$ (a)_0 = 1 $(空積)とする。

$ (a)_n $は「$ a $から$ 1 $ずつ増やしながら$ n $個掛けたもの」です。

次の値を計算せよ。
(1) $ (1)_3 $
(2) $ (3)_2 $
(3) $ (100)_0 $
(4) $ \left( \frac{1}{2} \right)_3 $

(1) $ (1)_3 = 1 \cdot 2 \cdot 3 = 6 $
(2) $ (3)_2 = 3 \cdot 4 = 12 $
(3) $ (100)_0 = 1 $
(4) $ \left( \frac{1}{2} \right)_3 = \frac{1}{2} \cdot \frac{3}{2} \cdot \frac{5}{2} = \frac{15}{8} $

定義から次のような性質が分かります:

ポッホハマー記号の性質

$ (1)_n = n! $
$ (a)_n = a \cdot (a + 1)_{n - 1}\ (n \geq 1) $
$ (a)_n = (a)_{n - 1} \cdot (a + n - 1)\ (n \geq 1) $
$ (a)_n = (- a - n + 1)_n \cdot (-1)^n $
$ _n \mathrm{P}_r = \frac{(1)_n}{(1)_{n - r}} = (n - r + 1)_{r} = (-n)_r (-1)^n $
$ _n \mathrm{C}_r = \frac{(1)_n}{(1)_r(1)_{n - r}} = \frac{(n - r + 1)_{r}}{(1)_{r}} = \frac{(-n)_r}{(1)_r}(-1)^n $

$ (5)_3 = 5 \cdot 6 \cdot 7 = (-7) \cdot (-6) \cdot (-5) \cdot (-1)^3 = (-7)_3 \cdot (-1)^3 $

超幾何級数

$ 0 $以上の整数$ r, s $と実数$ a_1, \cdots a_r, b_1, \cdots b_s, x $に対し、
$ \displaystyle \F{r}{s}{a_1, \cdots a_r}{b_1 \cdots b_s}{x} = \sum_{k = 0}^{\infty} \frac{(a_1)_k \cdots (a_r)_k}{(b_1)_k \cdots (b_s)_k} \frac{x^k}{k!} $
と定める。

$ x^k $の分母に$ k! = (1)_k $があるため、$ x^k $の係数として見ると$ s + 1 $個のポッホハマー記号が分母に乗ります。

$ r = 0 $のとき$ a_1, \cdots, a_r $は$ - $と表記します。$ s = 0 $のときの$ b_1, \cdots, b_s $も同様です。

超幾何級数は簡単に計算できるものばかりではないので問題を作りにくいですが、記号に慣れるために演習問題を用意しました。

$ \F{0}{0}{-}{-}{2} $を計算せよ。
$ \F{2}{1}{1,2}{1}{2} $は収束するか?
$ \F{2}{1}{1,1}{3}{1} $を計算せよ。

(1)
\begin{align*} & \F{0}{0}{-}{-}{2} \\ =& \sum_{k=0}^{\infty} \frac{2^k}{k!} \\ =& e^2 \end{align*}

(2)
$ \displaystyle \frac{(1)_k(2)_k}{(1)_k k!} = \frac{(2)_k}{k!} > 1 $であるから、
$ \displaystyle \F{2}{1}{1,2}{1}{2} = \sum_{k=0}^{\infty} \frac{(1)_k(2)_k}{(1)_k k!} 2^k $は発散する。

(3)
$ k \geq 2 $のとき
\begin{align*} & \frac{(1)_k(1)_k}{(3)_k k!} \\ =& \frac{1 \cdot 2 \cdot (3)_{k - 2} k!}{(3)_{k - 2} (k + 1)(k + 2) k!} \\ =& \frac{2}{(k + 1)(k + 2)} \\ =& \frac{2}{k + 1} - \frac{2}{k + 2} \end{align*}
である。
$ k = 0 $のとき$ \frac{(1)_k(1)_k}{(3)_k k!} = \frac{1}{1} = \frac{2}{1} - \frac{2}{2} $、
$ k = 1 $のとき$ \frac{(1)_k(1)_k}{(3)_k k!} = \frac{1}{3} = \frac{2}{2} - \frac{2}{3} $が成り立つので、
有限の$ n $に対して
\begin{align*} & \sum_{k = 0}^{n} \frac{(1)_k(1)_k}{(3)_k}\frac{1^k}{k!} \\ =& \sum_{k = 0}^{n} \left( \frac{2}{k + 1} - \frac{2}{k + 2} \right) \\ =& \left( \frac{2}{1} - \frac{2}{2} \right) + \left( \frac{2}{2} - \frac{2}{3} \right) + \cdots + \left( \frac{2}{n + 1} - \frac{2}{n + 2} \right) =& \frac{2}{1} - \frac{2}{n + 2} \end{align*}
である。この極限を取って
$ \displaystyle \F{2}{1}{1,1}{3}{1} = \frac{2}{1} = 2 $
を得る。

二項定理

実数$ x $と$ 0 $以上の整数$ n $に対し、
$ (1 + x)^n = \F10{-n}{-}{-x} $
が成り立つ。

$ r > n $のとき$ {}_n \mathrm{C}_r = 0 $とすれば、
\begin{align*} (1 + x)^n &= \sum_{k = 0}^{\infty} {}_n \mathrm{C}_rk x^k \\ &= \sum_{k = 0}^{\infty}\frac{(-n)_k}{(1)_k}(-1)^k x^k \\ &= \sum_{k = 0}^{\infty}\frac{(-n)_k}{1} \frac{(-x)^k}{k!} \\ &= \F10{-n}{-}{-x} \end{align*}

分数

かっこいい記号の準備ができたので問題を解いていきます。定理1を活用します。

定理1

$ 2 - bx $を$ 1 - bx + cx^2 (p, q \in \mathbb{R}) $で商が昇べきの順になるよう割ると、その商の$ n $次の項は$ a_n $である。

商の$ 0 $次の項は$ 2 = a_0 $である。この時点での余りは$ (2 - bx) - 2(1 - bx + cx^2) = bx - 2cx^2 $であるから、商の$ 1 $次の項は$ b = a_1 $である。
$ n \geq 2 $のときは定理1と数学的帰納法により従う。

よって、無限次の形式的な多項式として

$ \displaystyle \frac{2 - bx}{1 - bx + cx^2} = \sum_{k = 0}^{\infty} a_k x^k $

が成り立つことがわかりました。

次に、これが実際の等式として意味をなすことを証明します。
ここが一番の難所です。

$ |x| $が十分小さいとき、
$ \displaystyle \sum_{k = 0}^{\infty} a_k x^k $
は収束し、その値は
$ \displaystyle \frac{2 - bx}{1 - bx + cx^2} $
と等しい。

$ x^2 - bx + c = 0 $の解を$ \alpha, \beta (|\alpha| \geq |\beta|) $とする。
$ a_k $は$ k $によらない定数$ A, B $を用いて$ a_k = A {\alpha}^k + B {\beta}^k $と書けるので、
十分大きい$ k $に対し$ |a_k| < \gamma^k $となる正の実数$ \gamma $が存在する。
定理1の証明から、
$ (2 - bx) - (1 - bx + cx^2)(a_0x^0 + a_1x^1 + \cdots + a_kx^k) $
は$ k $に依存するある実数$ P, Q $を用いて
$ P x^{k+1} + Q x^{k+2} $
と書ける。
商の$ x^{k+1}, x^{k+2} $の係数を決める計算を考えると
$ P - a_{k+1} = 0, Q - (-b) a_{k+1} - a_{k+2} = 0 $
$ \therefore P = a_{k+1}, Q = (-b) a_{k+1} + a_{k+2} $
である。
$ |P| < \gamma^{k+1}, |Q| < (|b| + \gamma) \gamma^{k+1} $
であるから、$ |x| < \min\left(1, \frac{1}{\gamma}\right) $であれば、
\begin{align*} & \left| (2 - bx) - (1 - bx + cx^2)(a_0x^0 + a_1x^1 + \cdots + a_kx^k) \right| \\ =& |P| |x|^{k+1} + |Q| |x|^{k+2} \\ =& |P| |x|^{k+1} + |Q| |x|^{k+1} \cdot |x| \\ <& |P| |x|^{k+1} + |Q| |x|^{k+1} \\ <& (|b| + \gamma + 1) \gamma^{k + 1} |x|^{k + 1} \\ <& (|b| + \gamma + 1) (\gamma x)^{k + 1} \\ \rightarrow & 0\ (k \rightarrow \infty) \end{align*}
である。
さらに、$ 1 - bx + cx^2 $は連続なので$ |x| < \delta \Rightarrow \frac{1}{1 - bx + cx^2} < 2 $となる$ \delta > 0 $を取ることができ、
\begin{align*} & \left| \frac{2 - bx}{1 - bx + cx^2} - (a_0x^0 + a_1x^1 + \cdots + a_kx^k) \right| \\ <& 2 \left| (2 - bx) - (1 - bx + cx^2)(a_0x^0 + a_1x^1 + \cdots + a_kx^k) \right| \\ \rightarrow & 0\ (k \rightarrow \infty) \end{align*}
である。(Q.E.D.)

もう一つの表式

$ \frac{2 - bx}{1 - bx + cx^2} $の表式を、もう一つ得ます。そのために、無限等比級数の公式を利用します。

$ x $は絶対値が十分に小さく、考えている無限和が収束するように取るものとします。

\begin{align*} \frac{1}{1 - bx + cx^2} &= \frac{1}{1 - (bx - cx^2)} \\ &= 1 + (bx - cx^2) + (bx - cx^2)^2 \cdots \\ &= \sum_{m = 0}^{\infty} (bx - cx^2)^m \\ &= \sum_{m = 0}^{\infty} \left( \sum_{k = 0}^{\infty} {}_m \mathrm{C}_k (bx)^{m-k} (-cx^2)^{k} \right) \\ &= \sum_{m = 0}^{\infty} \left( \sum_{k = 0}^{\infty} {}_m \mathrm{C}_k b^{m-k} (-c)^{k} x^{m+k} \right) \\ \end{align*}

$ x $の次数でこれを整理します。$ m + k = n $とおくと、$ m = n - k $です。
$ k > \lfloor \frac{n}{2} \rfloor $のとき$ {}_{n - k} \mathrm{C}_k = 0 $なので、次のように変形できます。

\begin{align*} \frac{1}{1 - bx + cx^2} &= \frac{1}{1 - (bx - cx^2)} \\ &= \sum_{m = 0}^{\infty} \left( \sum_{k = 0}^{\infty} {}_m \mathrm{C}_k b^{m-k} (-c)^{k} x^{m+k} \right) \\ &= \sum_{n = 0}^{\infty} \left( \sum_{k = 0}^{\infty} {}_{n - k} \mathrm{C}_k b^{n-2k} (-c)^{k} x^n \right) \\ &= \sum_{n = 0}^{\infty} \left( \sum_{k = 0}^{\infty} {}_{n - k} \mathrm{C}_k b^{n-2k} (-c)^{k} x^n \right) \\ &= \sum_{n = 0}^{\infty} \left( \sum_{k = 0}^{\infty} \frac{(n - 2k + 1)_{k}}{(1)_{k}} \left(-b^{-2}c\right)^{k} (bx)^n \right) \end{align*}

$ \displaystyle U_n = \sum_{k = 0}^{\infty} \frac{(n - 2k + 1)_{k}}{(1)_{k}} \left(-b^{-2}c\right)^{k} b^n $とすると、

\begin{align*} a_n &= 2 U_n - b U_{n-1} \\ &= 2\sum_{k = 0}^{\infty} \frac{(n - 2k + 1)_{k}}{(1)_{k}} \left(-b^{-2}c\right)^{k} b^n - b \sum_{k = 0}^{\infty} \frac{(n - 2k)_{k}}{(1)_{k}} \left(-b^{-2}c\right)^{k} b^{n-1} \\ &= \sum_{k = 0}^{\infty} \left(\frac{2 (n - 2k + 1)_{k}}{(1)_{k}} - \frac{(n - 2k)_{k}}{(1)_{k}} \right) \left(-b^{-2}c\right)^{k} b^n \\ &= \sum_{k = 0}^{\infty} \left(\frac{2 (n - 2k + 1)_{k} - (n - 2k)_{k}}{(1)_{k}}\right) \left(-b^{-2}c\right)^{k} b^n \\ &= b^n + \sum_{k = 1}^{\infty} \left(\frac{2 (n - 2k + 1)_{k} - (n - 2k)_{k}}{(1)_{k}}\right) \left(-b^{-2}c\right)^{k} b^n \\ &= b^n + \sum_{k = 1}^{\infty} \left(\frac{2 (n - 2k + 1)_{k - 1} (n - k) - (n - 2k + 1)_{k - 1} (n - 2k)}{(1)_{k}}\right) \left(-b^{-2}c\right)^{k} b^n \\ &= b^n + \sum_{k = 1}^{\infty} \left(\frac{n (n - 2k + 1)_{k - 1}}{(1)_{k}}\right) \left(-b^{-2}c\right)^{k} b^n \\ &= n \sum_{k = 0}^{\infty} \left(\frac{(n - 2k + 1)_{k - 1}}{(1)_{k}}\right) \left(-b^{-2}c\right)^{k} b^n \\ &= n \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} \left( \frac{(-1)^k (n-k-1)!}{k! (n-2k)!} b^{n-2k} c^k \right) \\ \end{align*}
よって
$ \displaystyle A_n = (-1)^n a_n = (-1)^n n \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} \left( \frac{(-1)^k (n-k-1)!}{k! (n-2k)!} b^{n-2k} c^k \right) $
(Q.E.D.)

超幾何級数

せっかくなのでかっこいい記法に書き直してみましょう。

\begin{align*} A_n &= (-1)^n n \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} \left( \frac{(-1)^k (n-k-1)!}{k! (n-2k)!} b^{n-2k} c^k \right) \\ &= (-b)^n n \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} \frac{(-1)^k (n-k-1)!}{(n-2k)!} \frac{\left(b^{-2}c\right)^k}{k!} \\ \end{align*}

ここで
$ \displaystyle (n - k - 1)! = \frac{(n - 1)!}{(n - k)_k} = (n - 1)!\frac{(-1)^k}{(-n + 1)_k} $
\begin{align*} (n - 2k)! &= n! \frac{(-1)^{2k}}{(-n)_{2k}} \\ &= n! \frac{(-1)^{2k}}{\frac{-n}{2} \cdot \frac{-n+2}{2} \cdot \cdots \cdot \frac{-n+2k-1}{2} \cdot 2^{2k}} \\ &= n! \frac{(-1)^{2k}}{\left(\frac{-n}{2}\right)_k \left(\frac{-n+1}{2}\right)_k 2^{2k}} \\ \end{align*}
であるから
\begin{align*} A_n &= (-b)^n n \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} \frac{(-1)^k (n-k-1)!}{(n-2k)!} \frac{\left(b^{-2}c\right)^k}{k!} \\ &= (-b)^n n \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} \frac{(-1)^k (n-1)!(-1)^k \left(\frac{-n}{2}\right)_k \left(\frac{-n+1}{2}\right)_k 2^{2k}}{(-n+1)_k n! (-1)^{2k}} \frac{\left(b^{-2}c\right)^k}{k!} \\ &= (-b)^n n \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} \frac{\left(\frac{-n}{2}\right)_k \left(\frac{-n+1}{2}\right)_k}{n(-n+1)_k} \frac{\left(4b^{-2}c\right)^k}{k!} \\ &= (-b)^n \sum_{k = 0}^{\lfloor \frac{n}{2} \rfloor} \frac{\left(\frac{-n}{2}\right)_k \left(\frac{-n+1}{2}\right)_k}{n(-n+1)_k} \frac{\left(4b^{-2}c\right)^k}{k!} \\ &= (-b)^n \F{2}{1}{\frac{-n}{2}, \frac{-n+1}{2}}{-n+1}{\frac{4c}{b^2}} \end{align*}