三角形の垂心が満たす性質についての考察

216

この記事は，日曜数学アドベントカレンダー2023の12月19日の記事として作成しています．
日曜数学アドベントカレンダー2023

三角形の垂心の性質について

Wikipediaの垂心のページに，次のような記載があります．

三角形の垂心で交わる３本の頂垂線によって作られる６つの角には、図のように当該三角形の３つの角が２つずつ含まれる。また、三角形の各辺を頂垂線との交点で分割し、分割後のそれぞれの長さの辺を持つ正方形を作り（６つ）、図のように時計回りに赤・青・赤・青・赤・青とグループ分けして、赤と青の面積を求めると、両面積は等しくなっている。

これを図示すると下のようになります．

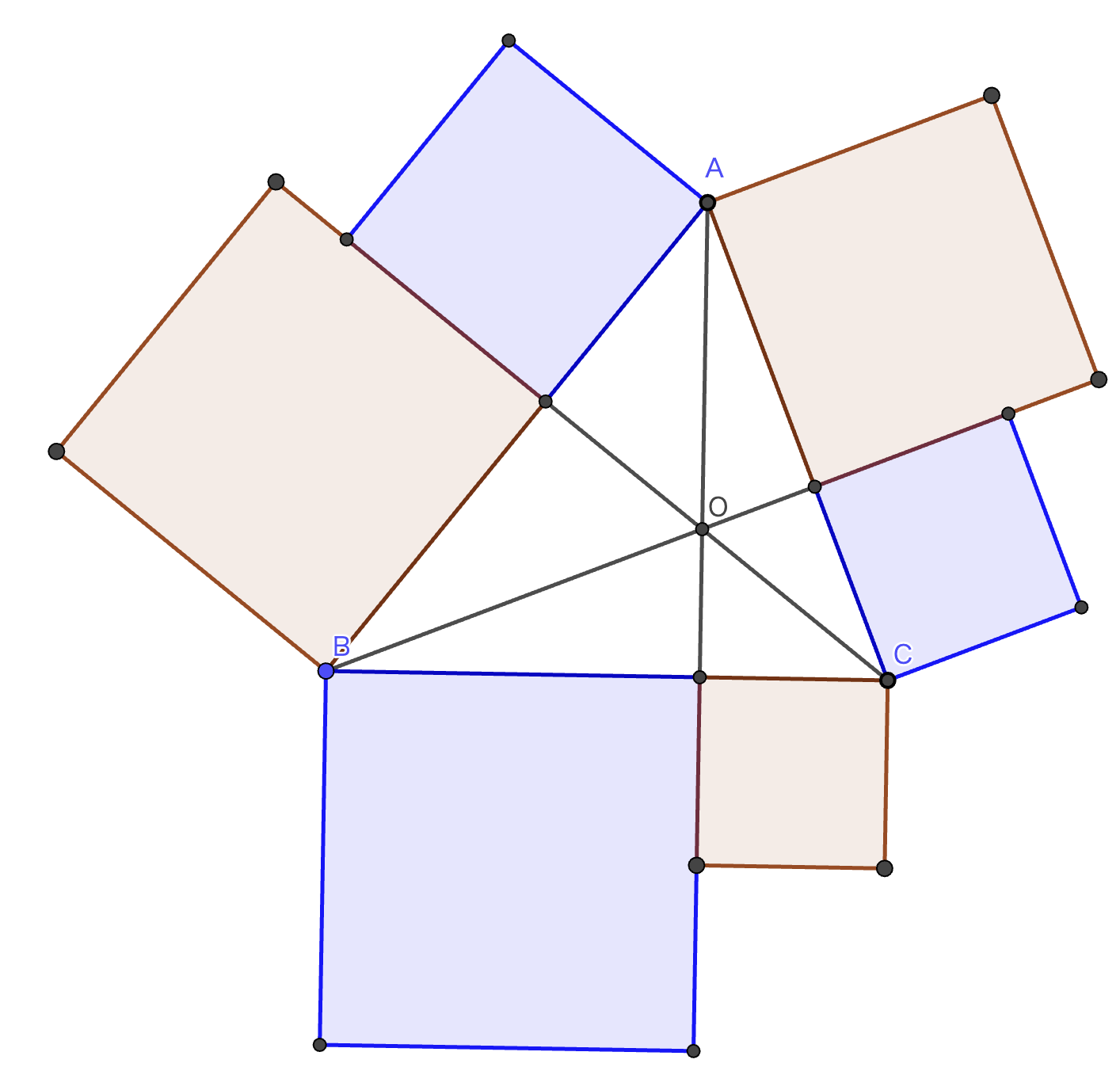
ここで，垂心の書き方を確認します．

三角形の各頂点から，対辺に向かって垂線をひく
1．で引いた3本の垂線の交点（必ず1点で交わる）が垂心である．

では次のような問題を考えるとどうなるでしょうか？
※ 以下，鋭角三角形のみを考えることとします．鈍角三角形でも符号付き面積を考えれば同じことが成り立つかもしれませんが，そこまで検討できていません．

三角形ABCの内部に点Pをとる．点Pから三角形の各辺に対して垂線をひき，三角形の各辺を分割する．（先ほどと同じように）三角形の外側に6個の正方形を作る．（先ほどと同じように色付けをしたとき）赤と青の正方形の面積は等しいか？

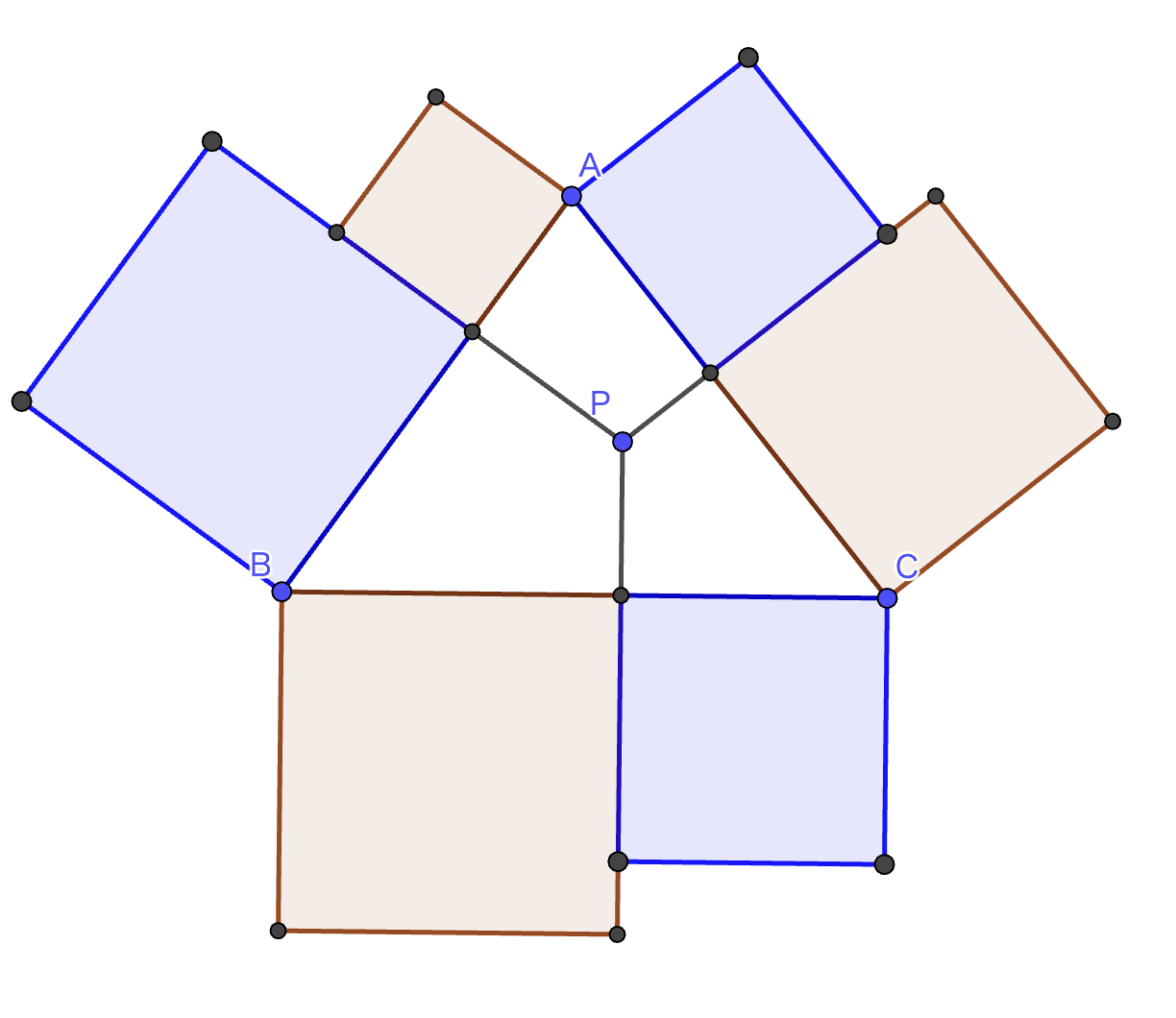点Pは三角形内部の任意の点

三角形ABCの内部に点Pをとる．三角形の各頂点と点Pを結ぶ3本の直線と三角形の各辺の交点により，三角形の各辺を分割する．（先ほどと同じように）三角形の外側に6個の正方形を作る．（先ほどと同じように色付けをしたとき）赤と青の正方形の面積は等しいか？

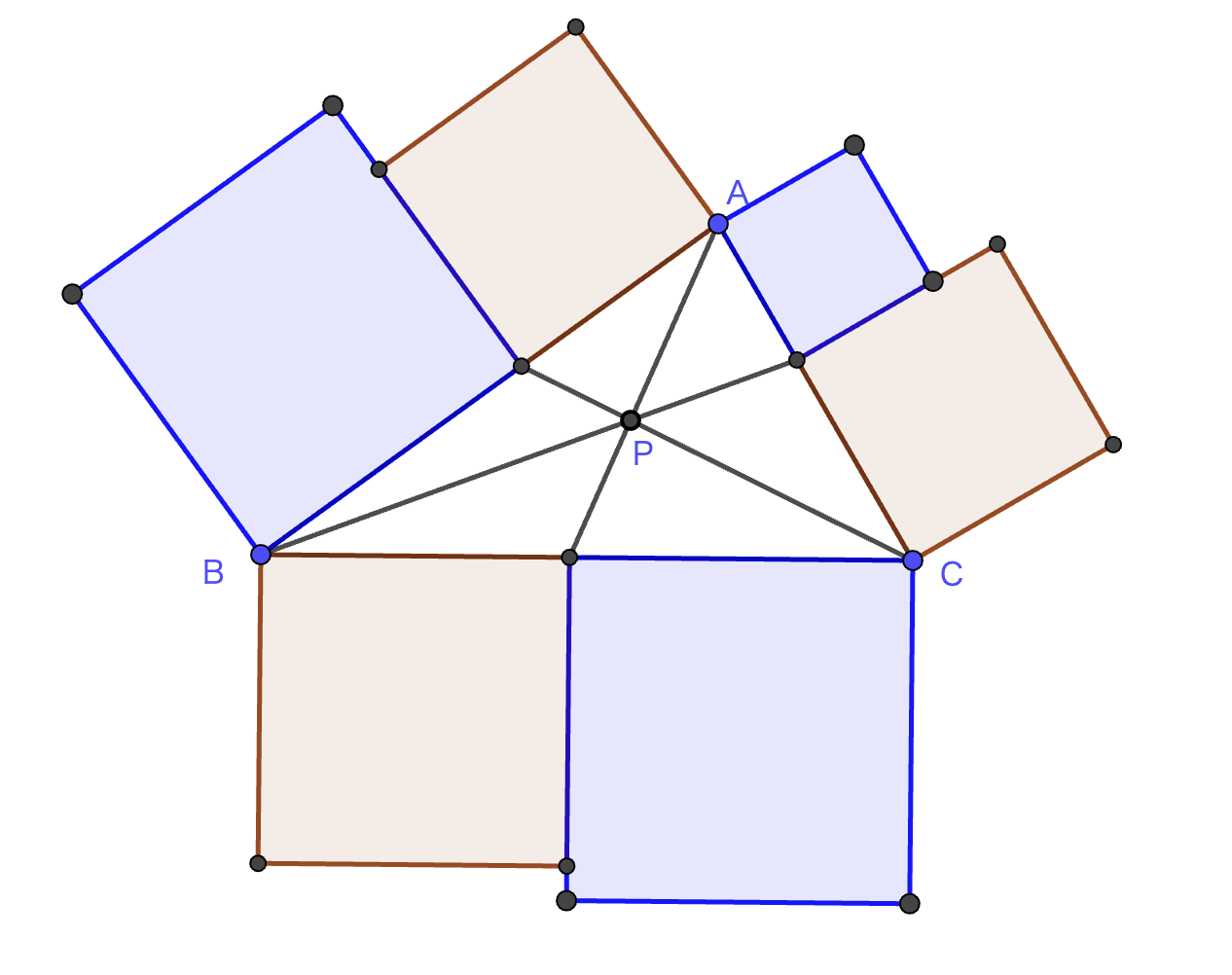点Pは三角形の内部の点

問題1，問題2ともに（赤い正方形の面積）=（青い正方形の面積）となるのでしょうか．それともいずれか一方（または両方とも）で，上記の関係は成立しないのでしょうか．

まず問題1から考えます。GeoGebra等のソフトを使って，少し実験や観察をすれば次のことが予想できます。
動かせる図2へのリンク

三角形ABCの内部に点Pをとる．点Pから三角形の各辺に対して垂線をひき，三角形の各辺を分割する．（先ほどと同じように）三角形の外側に6個の正方形を作る．（先ほどと同じように色付けをしたとき）赤と青の正方形の面積は等しい.

次のように3点A,B,Cをとり，三角形ABCとその内部の点Pについて考える．
$A(a,0)$,$B(b,0)$,$C(0,c)$.ただし，$a<0,b>0,c>0$．
点Pから各辺に下ろした垂線の足を$D,E,F$とする．
また，点Pは$P(X,Y)$とする．
すると，$$D(X,0)$$
$$E\left(\dfrac{b}{b^2+c^2}(c^2+bX-cY),\dfrac{c}{b^2+c^2}(b^2-bX+cY)\right)$$
$$F\left(\dfrac{a}{a^2+c^2}(c^2+aX-cY),\dfrac{c}{a^2+c^2}(a^2-aX+cY)\right)$$
となる．ここから6つの正方形の面積を計算すると，（赤の正方形の面積）=(青の正方形の面積)が成り立つことがわかる．

つづいて，問題2についても考えると，やはり簡単な観察により，こちらは（赤の正方形の面積）$\neq$(青の正方形の面積)となることがわかります．
動かせる図3へのリンク
そこで，次の問題をあらためて考えることにします．

三角形ABCの内部に点Pをとる．三角形の各頂点と点Pを結ぶ3本の直線と三角形の各辺の交点により，三角形の各辺を分割する．（先ほどと同じように）三角形の外側に6個の正方形を作る．（先ほどと同じように色付けをしたとき）赤と青の正方形の面積が等しくなるような点Pの軌跡はどのようになるか．

問題1のときと同じように三角形ABCや点Pの座標をとる．
$D$，$E$，$F$は次のようになる．
$$D\left(\dfrac{c X}{c-Y}, 0\right)$$
$$E\left( \dfrac{b(ac-cX-aY)}{ac-cX-bY},\dfrac{c(a-b)Y}{ac-cX-bY} \right)$$
$$F\left(\dfrac{a(bc-cX-bY)}{bc -cX-aY},\dfrac{c(-a+b)Y)}{bc-cX-aY}\right)$$
ここから，６つの正方形の面積を計算し，(赤の正方形の面積)=(青の正方形の面積)となるような$P(X,Y)$の条件を求めると，
$$a c y^3+b c y^3+2 c^2 x y^2-3 a b x y^2-2 a c^2 y^2-2 b c^2 y^2+a^2 b y^2+a b^2 y^2-2 a c x^2 y-2 b c x^2 y-2 c^3 x y+2 a^2 c x y+4 a b c x y+2 b^2 c x y+a c^3 y+b c^3 y-2 a^2 b c y-2 a b^2 c y-c^2 x^3+2 a c^2 x^2+2 b c^2 x^2-a^2 c^2 x-3 a b c^2 x-b^2 c^2 x+a^2 b c^2+a b^2 c^2=0$$
という式を得ます．（困った．．．）
困ったときのGeoGebraなので，とりあえず描いてみました．(緑の曲線)

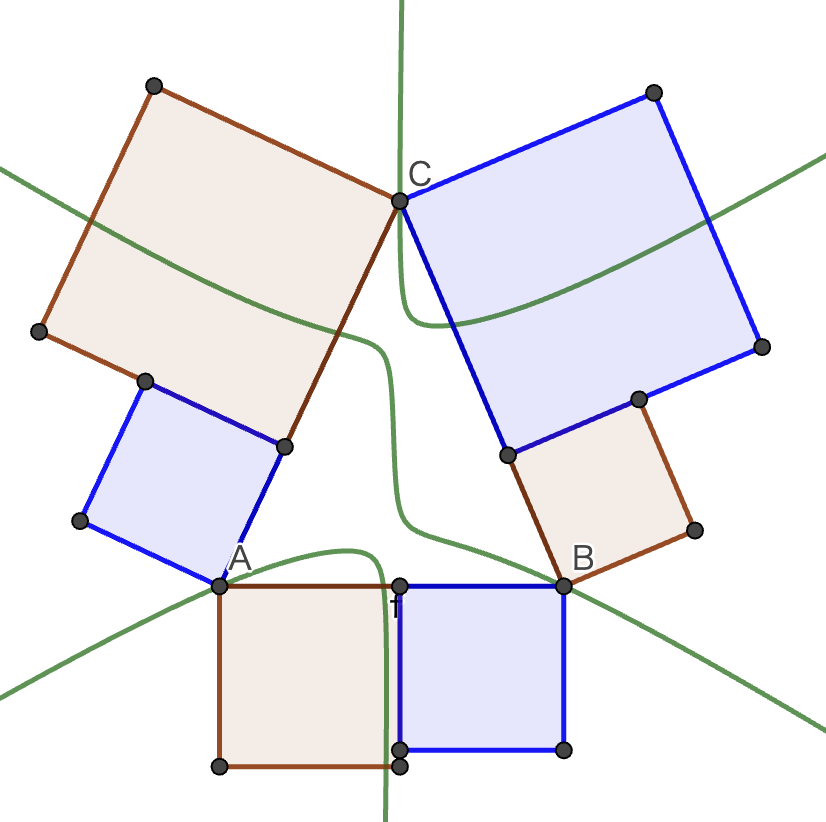
3本の曲線があり，うち2本は双曲線のように見えます．さきほどの式がうまく因数分解できて，3本の曲線の方程式がわかると嬉しかったのですが，うまくいきませんでした．（どなたかわかる方，お知らせください）

そこで，簡単な値に限定してもう少し考えてみることにしました．

簡単な条件

$a=-1$，$b=1$のときの点Pの軌跡の方程式を求めよ．

素直に先ほどの式に代入して計算すると次を得ます．
$$x(9y^-6\sqrt{3}y+3-x^2)=0 $$
図示すると，このようになります．
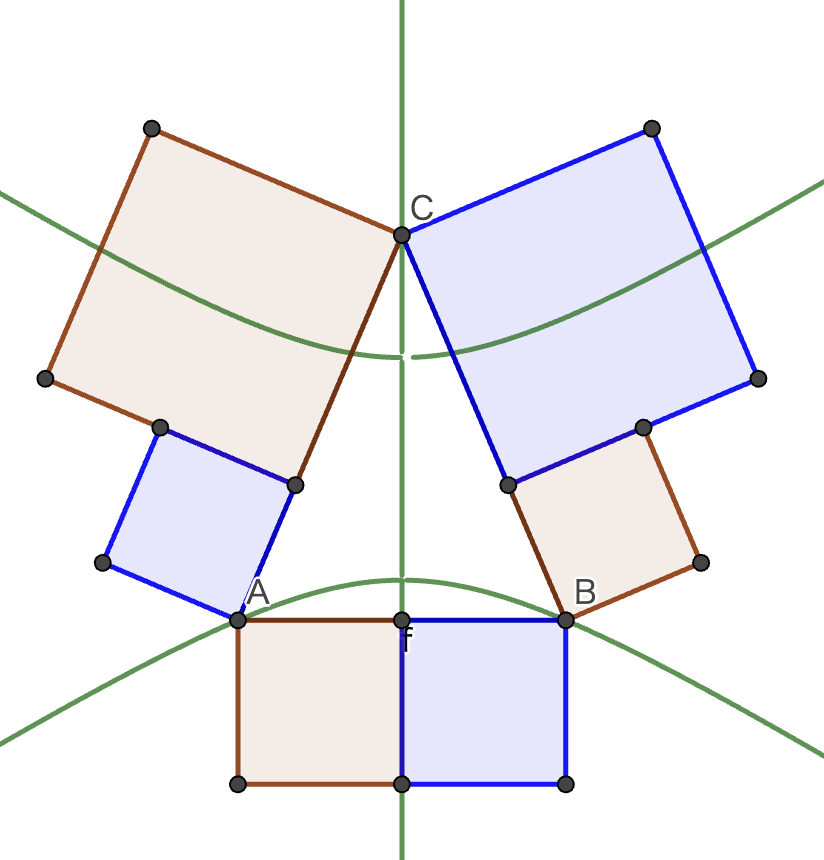a=-1,b=1

もう少し条件を緩めて，$a=-b$とすると，次のような式を得ます．
$$x((3+2c^2)y^2-2c^3y+c^2-c^2x^2)=0$$
※ 図示の結果はほぼ同じのため省略．
ちなみに，この双曲線について
焦点$\left(0,\dfrac{c^3}{3b^2+2c^2}+\sqrt{3(b^2+c^2)}\right)$,$\left(0,\dfrac{c^3}{3b^2+2c^2}-\sqrt{3(b^2+c^2)}\right)$

漸近線は$\dfrac{y-\frac{c^3}{3b^2+2c^2}}{c}\pm\dfrac{x}{\sqrt{3b^2+2c^2}}=0$
である．