母関数と漸化式

　この記事は以下の問題を解くことを目標にします。

例題をいくつか解きましょう。

例題.1

　条件をみたしながら $k$ 回に分けて玉を合計 $n$ 個入れるとき, $1,2,\dots,k$ 回目に入れた玉の個数を $c_1,c_2,\cdots,c_k$ とすると,

• $c_1+c_2+\cdots c_k=n$
• $c_i\equiv 1,2 \pmod{6}\quad(i=1,2,\cdots,k)$
  を満たす正整数の組 $(c_1,c_2,\cdots,c_k)$ の個数を数え上げる問題になります.
  よって, $k$ を固定した時の答えは以下の$x^n$ の係数になります.
  $$\begin{aligned} &\Big(\sum_{\substack{n\equiv 1,2 \pmod 6\\\ n\geq 0}}x^n\Big)^k\\ &=(x+x^2+x^7+x^8+\cdots)^k\\ &=\big(x(1+x^6+x^{12}+\cdots)+x^2(1+x^6+x^{12}+\cdots)\big)^k\\ &=\Big(x\frac{1}{1-x^6}+x^2\frac{1}{1-x^6}\big)^k\\ &=\Bigr(\frac{x+x^2}{1-x^6}\Bigl)^k \end{aligned}$$
  　答えはこれを $k=0,1,2,\cdots$ にて, 和を取れば求まるので, 先に母関数の和を取った以下の $x^n$ の係数になります.
  $$ \begin{aligned} \sum_{k=0}^{\infty}\Bigr(\frac{x+x^2}{1-x^6}\Bigl)^k &=\frac{1}{1-\frac{x+x^2}{1-x^6}}\\\\ &=\frac{1-x^6}{1-x-x^2-x^6} \end{aligned} $$
  　上の冪級数を $\displaystyle\sum_{k=0}^{\infty}a_kx^k$ とすると, 以下が成立します. ( $n\lt 0$ について, $a_n=0$ とします.)
  $$(1-x-x^2-x^6)\sum_{k=0}^{\infty}a_kx^k=\sum_{k=0}^{\infty}(a_k-a_{k-1}-a_{k-2}-a_{k-6})x^k$$
  　一方これは
  $$\dfrac{x+x^2}{1-x-x^2-x^6}\times(1-x-x^2-x^6)=1-x^6$$
  であるため,
  $$\sum_{k=0}^{\infty}(a_k-a_{k-1}-a_{k-2}-a_{k-6})x^k=1-x^6$$
  の $x^k$ の係数を比較することで, $k\not \in \{0,6\}$ にて,漸化式
  $$a_k-a_{k-1}-a_{k-2}-a_{k-6}=0$$
  が成立します. (問題の表記に従うと$f(n)-f(n-1)-f(n-2)-f(n-6)=0$ となります. )
  これは数直線上での $(x) \rightarrow (x+6n+1),(x+6m+2)$ のワープの問題と考えることもできます.次は座標平面の問題を考えてみます.

例題.2

　先程の問題と同じくまずワープを行う回数を $k$ 回と固定します. $1,2,\dots,k$ 回目に宣言した整数の組を $(x_1,y_1),(x_2,y_2),\cdots,(x_k,y_k)$ とすると,

• $(x_1,y_1)+(x_2,y_2)+\cdots (x_k,y_k)=(N,M)$
• $(x_i,y_i)\neq 0\quad(i=1,2,\cdots,k)$
  を満たす$\mathbb{Z}_{\geq 0}^2$の組 $((x_1,y_1),(x_2,y_2),\cdots,(x_k,y_k))$ の個数を数え上げる問題になります.
  よって, $k$ を固定した時の答えは以下の$x^Ny^M$ の係数になります.
  $$\begin{aligned} &\Big(\sum_{(n,m)\neq (0,0)}x^ny^m\Big)^k\\ &=\Big(\sum_{n,m \gt 0}x^ny^m-x^0y^0\Big)^k\\ &=\Big((1+x+x^2+\cdots)(1+y+y^2+\cdots)-1\Big)^k\\ &=\Big(\frac{1}{1-x}\frac{1}{1-y}-1\big)^k\\ &=\Bigr(\frac{x+y-xy}{(1-x)(1-y)}\Bigl)^k \end{aligned}$$
  　これを $k=0,1,2,\cdots$ にて, 和を取れば
  $$ \begin{aligned} &\sum_{k=0}^{\infty}\Bigr(\frac{x+y-xy}{(1-x)(1-y)}\Bigl)^k\\\\ &=\frac{1}{1-\frac{x+y-xy}{(1-x)(1-y)}}\\\\ &=\frac{1-x-y+xy}{(1-x-y+xy)-(x+y-xy)}\\\\ &=\frac{1-x-y+xy}{1-2x-2y+2xy} \end{aligned} $$
  この冪級数を $\displaystyle\sum_{n,m}a_{n,m}x^ny^m$ とすると, 分母の式 $1-2x-2y+2xy$ をかけることで,
  $$\sum_{n,m}(a_{n,m}-2a_{n-1,m}-2a_{n,m-1}+2a_{n-1,m-1})x^ny^m=1-x-y+xy $$
  が成立し, $(n,m)\not \in \{(0,0),(1,0),(0,1),(1,1)\}$ にて, $x^ny^m$ の係数を比較することで、
  $$a_{n,m}-2a_{n-1,m}-2a_{n,m-1}+2a_{n-1,m-1}=0$$
  すなわち,
  $$f(N,M)-2f(N-1,M)-2f(N,M-1)+2f(N-1,M-1)=0$$
  が得られます.
  余談ですが, $$f(N,M)=\sum_{\substack{n\leq N,m\leq M \\\ (n,m)\neq (N,M)}}f(n,m)$$ であり,
  $$2f(N,M)=\sum_{\substack{n\leq N,m\leq M \\\ (n,m)\neq (N,M)}}f(n,m)+f(N,M)=\sum_{n\leq N,m\leq M}f(n,m)$$
  が成り立ち,
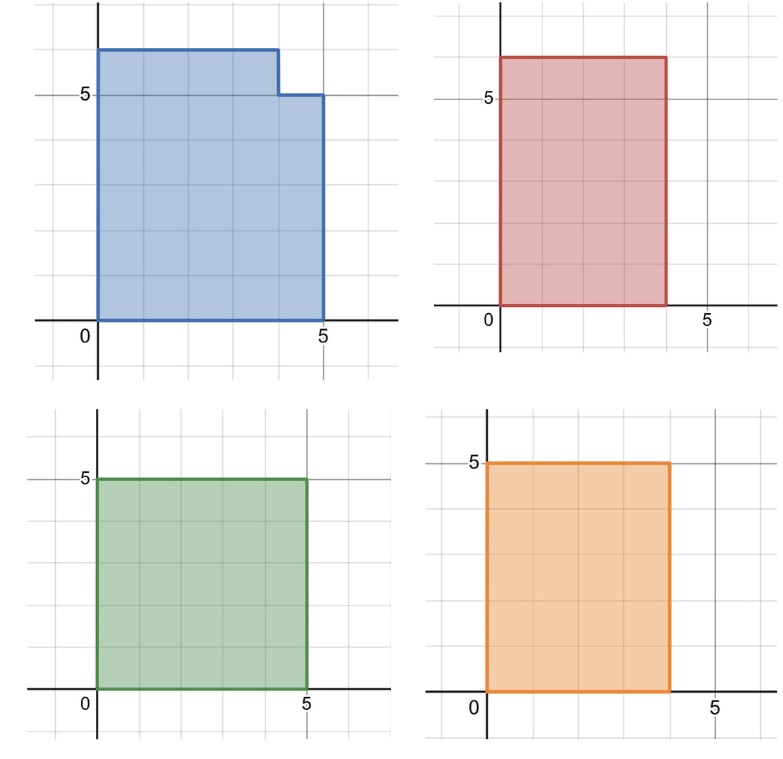
  図のように以下の式の項とそれぞれ対応を取ると実際に成り立つことがわかります.
  $${\color{blue}f(N,M)}={\color{red}2f(N-1,M)}+{\color{green}2f(N,M-1)}-{\color{orange}2f(N-1,M-1)}$$
  
  では本題を解いてみます.

本題

これまでと同様に考えると宣言することのできる整数組の集合を $S$ とすると $f(N,M)$ は
$$ \frac{1}{1-\displaystyle\sum_{(n,m)\in S}x^ny^m} $$
の $x^Ny^M$ の係数となります.
$$S=\{(n,m)\in \mathbb{Z}_{\geq 0}^2|\min(n,m)\equiv 1\pmod{2}\}$$
について, $\sum_{(n,m)\in S}x^ny^m$ を求めてみましょう.
$\min(i,j)=k$ となる $(i,j)$ について, 単項式 $x^iy^j$ の和をとると以下のようになります.
$$ \begin{aligned} \sum_{\min(i,j)=k}x^iy^j&=\sum_{\min(i,j)\geq k}x^iy^j-\sum_{\min(i,j)\geq k+1}x^iy^j\\\\ &=\sum_{\min(i,j)\geq 0}x^{k+i}y^{k+j}-\sum_{\min(i,j)\geq 0}x^{k+1+i}y^{k+1+j}\\\\ &=x^ky^k\sum_{\min(i,j)\geq 0}x^{i}y^{j}-x^{k+1}y^{k+1}\sum_{\min(i,j)\geq 0}x^{i}y^{j}\\\\ &=\frac{x^ky^k}{(1-x)(1-y)}-\frac{x^{k+1}y^{k+1}}{(1-x)(1-y)}\\\\ &=\frac{(1-xy)}{(1-x)(1-y)}x^ky^k \end{aligned} $$
したがって,
$$ \begin{aligned} \sum_{(n,m)\in S}x^ny^m&=\sum_{k=0}^{\infty}\sum_{\min(n,m)=2k+1}x^ny^m\\ &=\sum_{k=0}^{\infty}\frac{(1-xy)}{(1-x)(1-y)}(xy)^{2k+1}\\ &=\frac{(1-xy)}{(1-x)(1-y)}\frac{xy}{1-x^2y^2}\\ &=\frac{xy}{(1-x)(1-y)(1+xy)} \end{aligned} $$
これより,
$$ \begin{aligned} \frac{1}{1-\displaystyle\sum_{(n,m)\in S}x^ny^m}&=\frac{1}{1-\displaystyle\frac{xy}{(1-x)(1-y)(1+xy)}}\\ &=\frac{(1-x)(1-y)(1+xy)}{(1-x)(1-y)(1+xy)-xy}\\ &=\frac{1-x-y+2xy-x^2y-xy^2+x^2y^2}{1-x-y+xy-x^2y-xy^2+x^2y^2} \end{aligned}}
$$ したがって, $(N,M)\not\in \{ (0,0),(1,0),(0,1),(1,1),(2,1),(1,2),(2,2)\}$ にて $f(N,M)-f(N-1,M)-f(N,M-1)+f(N-1,M-1)-f(N-2,M-1)-f(N-1,M-2)+f(N-2,M-2)=0$ が成立します. 母関数を用いずに導出する方法を思いついた方がいらっしゃいましたら教えてください！ここまで読んでくださりありがとうございました！！