極限ってなに？

前書き

初めましての方は初めまして。今回は高校数学における｢極限｣の話をしたいと思います。なんでこんなことしてるかって言うと、ベクトル解析の記事で高校までの微積分の記事を書くと言ってしまったからです。でもいきなり高校までの微積分の話は書けないので極限から書くことにしました。この記事は完全に中高生向けとなっております。あとは大学受験が終わった春から大学に通う皆様ですね。復習にちょうどいいと思うのでぜひ読んでください。

極限ってなに？

簡単に言うと「ある関数f(x)を考える時、xがある数値aに近付いたときのf(x)の値」を指します。(数列でも極限を使う時がありますがそれはまた別の機会にでも....)

表記とか具体例とか

極限を考える時はlimを使います。limit(極限)です。わかりやすいね。極限というものは微分の時に必須の考え方なのでぜひ覚えて帰ってください。
たとえば$\lim_{n \to \infty}$とか$\lim_{n \to 0}$みたいに描きますノートとかだったらlimの下にだいたい描きます。
例を使って考えてみましょう。
$\lim_{x \to \infty} 1/x$ のような極限があったとします。xを正の方向へ動かしてみましょう。
x=1の時は1,x=100の時は1/100,x=10000の時は1/10000です。xが大きくなっていくと、1/xはだんだん小さくなっていくのが分かりますね。グラフを見ても一目瞭然ですね。 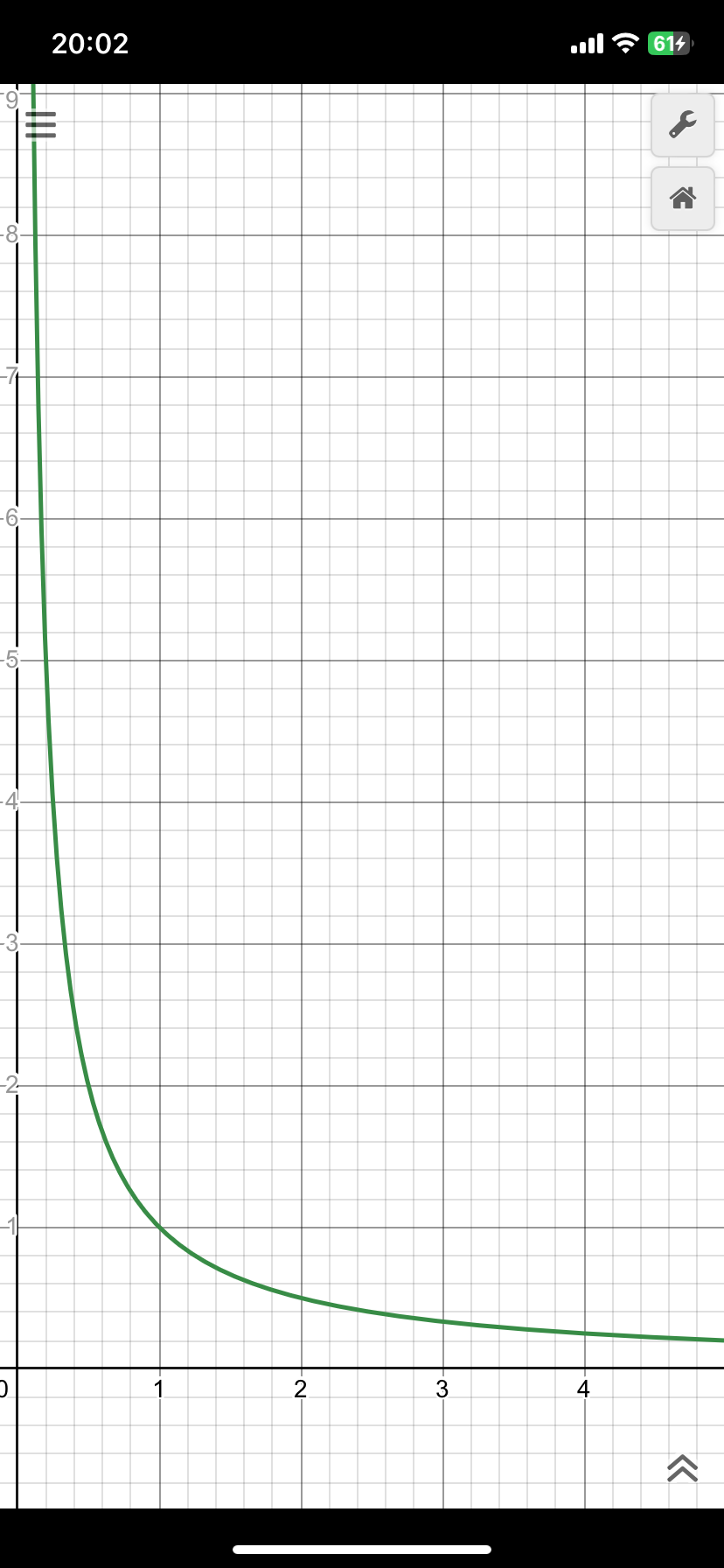y=1/xのグラフ

極限を扱う時の注意

極限と触れ合っているとたまに｢不定形｣というものが登場します。0/0とか∞-∞,∞/∞みたいな。
不定形というものが登場してしまっても嫌がらないであげてください。不定形自身も嫌っています。焦らずに解消してあげてください。
パターンを抑えてしまえば解消できるので極限を簡単に扱うことができるようになります。

①分母分子を約分

(1)$\lim_{x \to \infty}x^2/x$
(2)$\lim_{x \to \infty}x/x^3$
(1)のときは分母分子をxで割るだけで不定形を解消できます。
同じ要領でいくと(2)も分母分子をxで割るだけですね。
(1)は∞,(2)は0となります。(どちらもグラフを見るとわかります。)

②分子の実数化

$\lim_{x \to \infty}(\sqrt{x+1}-\sqrt{x})$などですね。xを極限に飛ばしてしまうと不定形になってしまいます。そういうときは分子の実数化をしましょう。
(与式)$=\lim_{x \to \infty}(\sqrt{x+1}-\sqrt{x})\times(\sqrt{x+1}+\sqrt{x})/(\sqrt{x+1}+\sqrt{x})$
$=\lim_{x \to \infty}1/(\sqrt{x+1}+\sqrt{x})$
$=0$

終わりに

今回は極限を扱いました。ちょっと短かったかも？微分積分の回は長くなると思います。それか前後編で分けます。積分で書く量がそこそこあるので。
というわけで極限の世界は一旦終わりになります。まあ微分の話でかなり出てくるんですけどね。ということで今回はここまで。ではまた会いましょう。