Nelsenによるヘロンの公式のエレガントな証明
ヘロンの公式
$ \triangle ABC$の3辺の長さを$a,b,c$, 面積を$S$とするとき,
$S=\sqrt{s(s-a)(s-b)(s-c)}.$ ただし, $\displaystyle s=\frac{a+b+c}{2}.$
余弦定理を用いた代数的な証明をよく見かけるが, これはまことに味気ない. 初等幾何による証明がいくつか知られているが複雑なものが多い(ヘロン自身の証明も初等幾何による). しかし, 20年以上前に現れたNelsenによる図形証明 (文献 [1])は非常にエレガントだ.
Nelsenによるエレガントな図形証明
この記事では, Nelsenの論文をベースにして, 少し読みやすく書き直したものを紹介する.
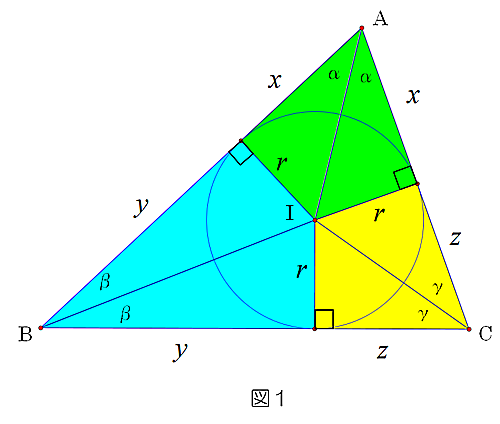
$\triangle ABC$の3辺の長さを$AB=c,BC=a,CA=b$, 内接円の半径を$r$とする. さらに, 図1のように長さ$x,y,z$と角度$\alpha,\beta,\gamma $を設定する.
このとき,$\ x+y+z=s,\ x+y=c,\ y+z=a,\ z+x=b$より, $x=s-a,\ y=s-b,\ z=s-c.$ また, $\displaystyle S=\frac{1}{2}r(a+b+c)=rs.$
 ヘロン1
ヘロン1
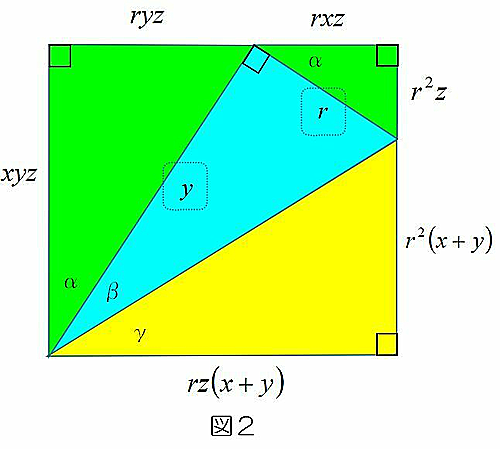
$\alpha+\beta+\gamma=90°$に注意すると, 図1の緑・青・黄と相似な三角形を図2のように組み合わせて長方形をつくることができる. その縦の長さに注目して
$xyz=r^2(x+y+z)=r^2s.$ よって, $\displaystyle 1=\frac{xyz}{r^2s}=\frac{sxyz}{(rs)^2}=\frac{s(s-a)(s-b)(s-c)}{S^2}$より $ \displaystyle S=\sqrt{s(s-a)(s-b)(s-c)}.$
 ヘロン2
ヘロン2
「Edwardsによるヘロンの公式の複素数を使った証明」も併せてご覧ください.
(参考文献)
[1] R. B. Nelsen, "Heron's formula via proofs without words", The College Mathematics Journal 32.4(2001)
