三角関数から複素平面までの流れを「逆さ」にしてみた
概要
高校の数学では三角比→三角比の特殊値→三角関数→複素数→複素平面の順で習うと思いますが、これを(だいたい)逆さにしてみました。
本文
複素数
$ i $を形式的な文字とし、剰余環$ \mathbb{R}[i]/(i^2+1) $を$ \mathbb{C} $と書く。$ \mathbb{C} $の元を複素数と呼ぶ。
任意の$ z \in \mathbb{C} $は$ a + bi (a, b \in \mathbb{R}) $の形に一意に表現できる。このとき、
- $ a $を$ z $の実部といい、$ \Re z $で表す。
- $ b $を$ z $の虚部といい、$ \Im z $で表す。
実部と虚部はともに実数である。
$ z \in \mathbb{C}, z = a + bi (a, b \in \mathbb{R}) $のとき、$ z $の絶対値を$ \sqrt{a^2 + b^2} $と定め、これを$ |z| $と書く。
$ z \in \mathbb{C}, z = a + bi (a, b \in \mathbb{R}) $のとき、$ z $の共軛を$ a - bi $と定め、これを$ \bar{z} $と書く。
文献によっては共軛のことを共役と書く。現代ではその方が一般的なので、この記事でもそのように書く。
文献によっては$ \bar{z} $を$ z^* $と書くが、この記事では採用しない。
$ z \bar{z} = (a + bi)(a - bi) = a^2 - b^2i^2 = a^2 + b^2 = |z|^2 $が成り立つ。
複素数$ z = a + bi, w = c + di (a, b, c, d \in \mathbb{R}) $の四則演算の結果は、以下の通りである:
- $ z + w = (a + c) + (b + d)i $
- $ z - w = (a - c) + (b - d)i $
- $ zw = (ac - bd) + (ad + bc)i $
- $ \frac{z}{w} = \frac{(a + bi)(c - di)}{(c + di)(c - di)} = \frac{(ac + bd) + (-ad + bc)i}{c^2 + d^2}\ (w \neq 0)$
複素平面
$ z \in \mathbb{C}, z = a + bi (a, b \in \mathbb{R}) $とする。このとき、$ z $の偏角$ \arg{z} $を、$ xy $平面上で$ \mathrm{O}(0, 0), \mathrm{P}(a, b)$を取ったときに、$ x $軸の正の部分と線分$ \mathrm{OP} $のなす角を$ x $軸の正の部分から反時計回りに測った角度と定める。
偏角は$ \arctan $などを用いて完全に代数的に定義することもできます。
$ 0 $の偏角は定義されないものとします。
$ \arg{z} $は加法群としての$ \mathbb{R} / 2\pi\mathbb{R} $の元と考えます。非整数倍が定義できませんが、これは意図した挙動です。
主定理
この記事で最も重要な定理を示します。あえて細かくやります。
$ z = i, w \in \mathbb{C} $とする。このとき、
- $ |zw| = |z| \cdot |w| $
- $ \arg{zw} = \arg{z} + \arg{w} $
が成り立つ。
$ w = c + di (c ,d \in \mathbb{R}) $とする。このとき、$ zw = -d + ci $であるが、点$ (-d, c) $は点$ (c, d) $を原点中心に$ \frac{\pi}{4} = \arg{z} $回転させたものであるから、これらが成り立つ。
$ n \in \mathbb{N}, z = i^n, w \in \mathbb{C} $とする。このとき、
- $ |zw| = |z| \cdot |w| $
- $ \arg{zw} = \arg{z} + \arg{w} $
が成り立つ。
定理1と数学的帰納法から示せる。
$ z, w \in \mathbb{C} $とする。このとき、
- $ |zw| = |z| \cdot |w| $
- $ \arg{zw} = \arg{z} + \arg{w} $
が成り立つ。
$ z = i^n \cdot z', w = i^m \cdot w' $、ただし
- $ n, m \in \mathbb{N} $
- $ \exists \theta \in \left[0, \frac{\pi}{2}\right)\ s.t.\ \theta \in \arg z' $
- $ \exists \varphi \in \left[0, \frac{\pi}{2}\right)\ s.t.\ \varphi \in \arg w' $
となるものが取れるのでそのような$ (n, m, \theta, \varphi) $を一つ取り固定する。
もし$ z', w' $について定理が成り立てば、
\begin{equation*} |zw| = |i^{n+m} z' w'| = |i^{n+m}| |z'w'| = |i^n||i^m||z'||w| = |i^n z'||i^m w'| = |z||w| \end{equation*}
\begin{align*} \arg{\left(zw\right)} &= \arg{\left(i^{n+m} z' w'\right)} \\ & = \arg{i^{n+m}}+\arg{z'}+\arg{w'} \\ &= \arg{i^n}+\arg{i^m}+\arg{z'}+\arg{w'} \\ &= \arg{\left(i^n z'\right)} + \arg{\left(i^m w'\right)} \\ &= \arg{z} + \arg{w} \end{align*}
であるから$ z, w $についても成り立つ。
$ z = 1 $または$ w = 1 $のときは明らかなので、$ \theta \neq 0, \varphi \neq 0 $とする。
$ z = a + bi, w = c + di (a, b, c, d \in \mathbb{R}) $とおく。
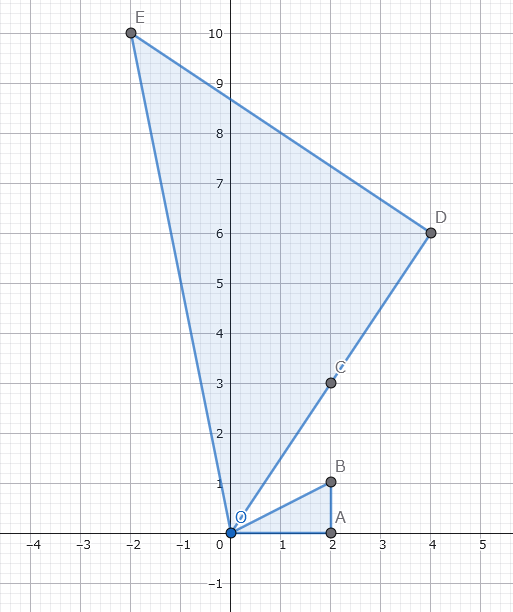
座標平面上に、$ \mathrm{O}(0, 0), \mathrm{A}(a, 0), \mathrm{B}(a, b), \mathrm{C}(c, d) $をとり、$ \mathrm{OC} $を$ \mathrm{C} $側に延長して$ \mathrm{OD} = \mathrm{OA} \cdot \mathrm{OC} $となる位置に$ \mathrm{D} $をとる。また、$ \mathrm{E}(ac - bd, ad + bc) $とする。
$ \mathrm{D}(ac, ad) $より、$ \overrightarrow{\mathrm{OD}} = (ac, ad), \overrightarrow{\mathrm{DE}} = (-bd, bc) $であるから、$ \overrightarrow{\mathrm{OD}} \cdot \overrightarrow{\mathrm{DE}} = -acbd + adbc = 0 $より$ \mathrm{OD} \perp \mathrm{DE} $である。
$ \mathrm{OA} : \mathrm{OD} = 1 : \mathrm{OC} = 1 : |w| $
$ \mathrm{AB} : \mathrm{DE} = b : b\sqrt{d^2 + c^2} = b : b|w| = 1 : |w| $
であるから、$ \triangle \mathrm{OAB} $と$ \triangle \mathrm{ODE} $について、$ 1 $つの角とそれを挟む$ 2 $辺の比がそれぞれ等しいので$ \triangle \mathrm{OAB} \sim \triangle \mathrm{ODE} $である。
よって$ \angle \mathrm{EOD} = \angle \mathrm{BOA} $なので、
$ \arg{(zw)} = \angle \mathrm{EOA} = \angle \mathrm{EOD} + \angle \mathrm{DOA} = \angle \mathrm{BOA} + \angle \mathrm{DOA} = \arg{z} + \arg{w} $
である。
三角関数
$ xy $平面上の原点を中心とする半径$ 1 $の円上を、点$ (1, 0) $から反時計回りに$ \theta $だけ進んだ点の$ x $座標を$ \cos{\theta} $、$ y $座標を$ \sin{\theta} $とする。
$ \cos^2{\theta} + \sin^2{\theta} = 1 $
円という図形の定義より自明。
実数$ \theta $に対して、$ \exp(i\theta) $を$ \cos{\theta} + i \sin{\theta} $と定める。このとき、$ \exp(i \theta) $は指数法則を満たす。すなわち、任意の実数$ \alpha, \beta $と自然数$ n $に対して
- $ \exp(i (\alpha + \beta)) = \exp(i \alpha) \cdot \exp(i \beta) $
- $ \exp(i (n \alpha)) = \left(\exp(i \alpha)\right)^n $
が成り立つ。
円の対称性と定理3から即座に従う。
ここまで来たらもう何でもできます。
$ \cos{3\theta} = 4\cos^3{\theta} - 3\cos{\theta} $
$ \sin{3\theta} = 3\sin{\theta} - 4\sin^3{\theta} $
\begin{align*} (\cos{\theta} + i\sin{\theta})^3 &= \cos^3{\theta} + 3i\cos^2{\theta}\sin{\theta} - 3\cos{\theta}\sin^2{\theta} - i\sin^3{\theta} \\ &= \cos^3{\theta} - 3\cos{\theta}(1 - \cos^2{\theta}) + 3i(1 - \sin^2{\theta})\sin{\theta} - i\sin^3{\theta} \\ &= (4\cos^3{\theta} - 3\cos{\theta}) + i(3\sin{\theta} - 4\sin^3{\theta}) \end{align*}
$ \cos{2\theta} = \cos^2{\theta} - \sin^2{\theta} $
$ \sin{2\theta} = 2\sin{\theta}\cos{\theta} $
\begin{align*} (\cos{\theta} + i\sin{\theta})^2 &= \cos^2{\theta} + 2i\cos{\theta}\sin{\theta} -\sin^2{\theta} \\ &= (\cos^2{\theta} - \sin^2{\theta}) + i(2\sin{\theta}\cos{\theta}) \end{align*}
$ \cos{(\alpha + \beta)} = \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta} $
$ \sin{(\alpha + \beta)} = \sin{\alpha}\cos{\beta} + \cos{\alpha}\cos{\beta} $
$ (\cos{\alpha} + i \sin{\alpha})(\cos{\beta} + i \sin{\beta}) = (\cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta}) + i(\sin{\alpha}\cos{\beta} + \cos{\alpha}\cos{\beta}) $
$ a \cos{\theta} + b \sin{\theta} = \sqrt{a^2 + b^2} \sin(\theta + \alpha) $
ただし$ \alpha = \arg{(b + ai)} $
$ z = b + ai, w = (\cos{\theta} + i\sin{\theta})(b + ai) $とすると
$ |w| = \sqrt{a^2 + b^2} $
$ \arg w = \theta + \alpha $
$ \Im w = a \cos{\theta} + b \sin{\theta} $(分配法則より)
(Q.E.D.)
特殊値
三角関数を複素数でぶん殴るのも楽しいですが、そろそろ特殊値を求めましょう。
$ \cos{\left( \frac{\pi}{2} + \theta \right)} = -\sin{\theta} $
$ \sin{\left( \frac{\pi}{2} + \theta \right)} = \cos{\theta} $
$ z = \cos{\theta} + i \sin{\theta} $とする。
$ \cos{\left( \frac{\pi}{2} + \theta \right)} = \Re (iz) = -\sin{\theta} $
$ \sin{\left( \frac{\pi}{2} + \theta \right)} = \Im (iz) = \cos{\theta} $
この定理より、$ 0 \leq \theta < \frac{\pi}{2} $の範囲で特殊値を求めればそこから範囲を広げて行けることがわかります。
$ \cos{0} = 1 $
$ \sin{0} = 0 $
$ \cos, \sin $の定義から明らか。
$ \cos{\frac{\pi}{2}} = 0, \cos{\pi} = -1 $
$ \sin{\frac{\pi}{2}} = 1, \sin{\pi} = 0 $
定理10より即座に従う。
$ \cos{\frac{\pi}{4}} = \frac{\sqrt{2}}{2} $
$ \sin{\frac{\pi}{4}} = \frac{\sqrt{2}}{2} $
$ \cos{\frac{\pi}{4}} = x, \cos{\frac{\pi}{4}} = y $とすると、$ x, y \in \mathbb{R} $かつ$ (x + yi)^2 = i $である。
$ (x + yi)^2 = (x^2 - y^2) + 2xyi $であるから、両辺の実部と虚部を比較して$ x^2 - y^2 = 0, 2xy = 1 $を得る。
$ x > 0, y > 0 $であるから$ x^2 - y^2 = 0 $より$ x = y $であり、よって$ 2x^2 = 2y^2 = 1 $すなわち$ x = y = \frac{\sqrt{2}}{2} $である。
$ \cos{\frac{\pi}{3}} = \frac{1}{2} $
$ \sin{\frac{\pi}{3}} = \frac{\sqrt{3}}{2} $
$ \theta = \frac{\pi}{3} $とすると、$ 3\theta = \pi $であるから$ 3 $倍角の公式より
$ 4\cos^3{\theta} - 3\cos{\theta} = -1 $
が成り立つ。
$ \cos{\theta} = x $とおくと
\begin{align*}
4x^3 - 3x &= -1 \\
4x^3 - 3x + 1 &= 0 \\
(x + 1)(4x^2 - 4x + 1) &= 0 \\
(x + 1)(2x - 1)^2 &= 0 \\
x &= -1, \frac{1}{2}
\end{align*}
$ \cos{\theta} > 0 $より、$ \cos{\frac{\pi}{3}} = \frac{1}{2} $である。
同様に$ \sin{\theta} = y $とおくと
\begin{align*}
3x - 4x^3 &= 0 \\
x(3 - 4x^2) &= 0 \\
x &= 0, \frac{\sqrt{3}}{2}
\end{align*}
$ \sin{\theta} > 0 $より、$ \sin{\frac{\pi}{3}} = \frac{\sqrt{3}}{2} $である。
$ \cos{\frac{\pi}{6}} = \frac{\sqrt{3}}{2} $
$ \sin{\frac{\pi}{6}} = \frac{1}{2} $
\begin{align*} \cos{\frac{\pi}{6}} + i\sin{\frac{\pi}{6}} &= \frac{i}{\cos{\frac{\pi}{3}} + i\sin{\frac{\pi}{3}}} \\ &= i\left(\cos{\frac{\pi}{3}} - i\sin{\frac{\pi}{3}}\right) \\ &= i\left(\frac{1}{2} - \frac{\sqrt{3}}{2}i\right) \\ &= \frac{\sqrt{3}}{2} + \frac{1}{2}i \end{align*}
三角比
$ \mathrm{B}$が直角の$ \triangle \mathrm{ABC} $において、$ \cos{\angle A} = \frac{AB}{AC}, \sin{\angle A} = \frac{CB}{AC} $が成り立つ。
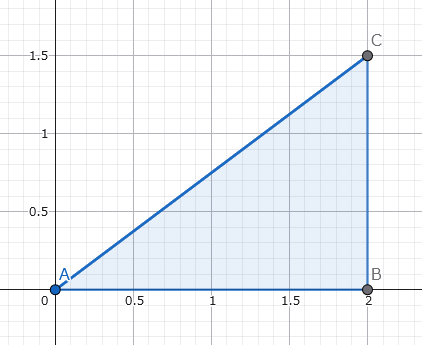
$ \mathrm{A} $を中心とし$ \mathrm{AC} $を半径とする円を描くことでわかる。
まとめ
複素数の図形的性質(定理3)を直交座標のまま示すことで、三角関数を複素数の簡単な計算にすることができ、最後に三角比を証明することもできました。
逆張りって楽しいですね。