特異点論入門〜これほど簡単な入門記事は多分ない〜スピンオフ

音沙汰ナクテってVtuberっぽい

続編は少々お待ちください...

皆々様,お久しぶりです.しんぎゅらです！！続編を書く書くと言いながら,音沙汰なくてすみません.
今回は,part2で紹介した

齋藤の

定理の

具体例を

紹介します

実はこの度,卒業研究発表会を無事完遂いたしまして,その際に調べた関数芽とその$\K$-軌道を紹介します.

本題

後々説明しますが$\K$-単純特異点(後ほど説明)の分類がある程度(私もどの程度か分かってない)研究されていて,有名なもので$A-D-E$のタイプは特異点論を勉強すれば耳にしないことはないでしょう.
今回説明するのは$E_{18}$-型特異点というものです.
\begin{align} f(x,y)=x^{3}+y^{10}+\sum_{10i+3j>30}a_{ij}x^{i}y^{j} \end{align}という冪級数を考えます.

さてこの$f$は実は$f_{a,b}(x,y)=x^{3}+y^{10}+axy^{7}+bxy^{8}$に$\R$-同値になります.(詳しくいうと,$\{a_{ij}\}$に対して$(a,b)\in\mathbb{R}^{2}$が存在して$\R$-同値)(これは気合いの計算と$10$-決定(後ほど説明)を用います)
$f_{a,b}$は$a,b$を動かすと関数としてめっちゃ変わりそうですが,実は$a,b$によらずMilnor数$\mu(f)$は$18$で一定なのです.更に$\K$-同値類もたったの3つになるのです.はい、もう激ヤバ確定〜〜
その同値類とは
$ \begin{eqnarray} \left\{ \begin{array}{ll} g_{1}=x^{3}+y^{10}+xy^{7}+xy^{8}&& (a\neq0) \\ g_{2}=x^{3}+y^{10}+xy^{8} &&(a=0,b\neq0) \\ g_{3}=x^{3}+y^{10} &&(a=b=0) \end{array} \right. \end{eqnarray} $
を代表元とする3つです.
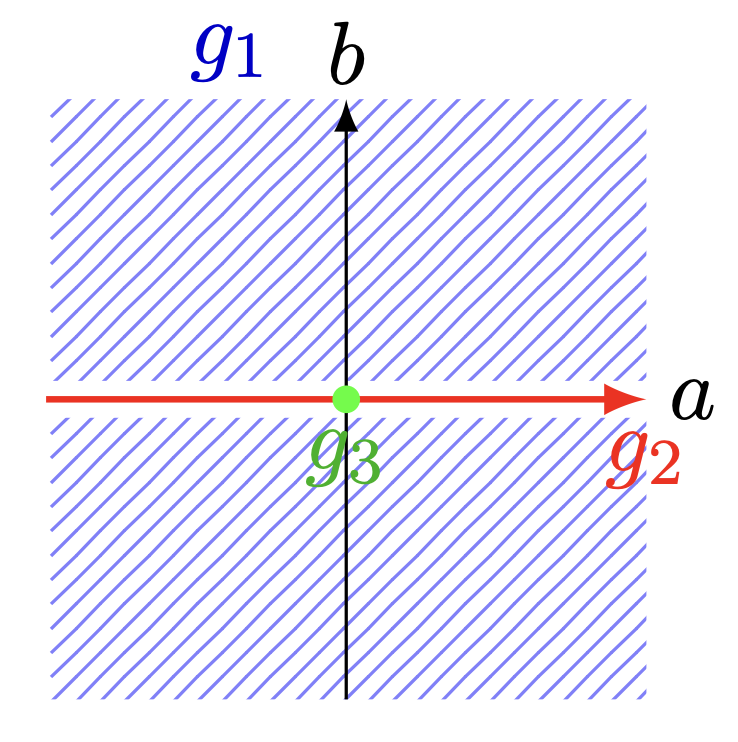同値類分布の様子(画像デカすぎ)
同値類が$3$つであることの証明はpart2で紹介した
$T(f)\cong T(g)\Rightarrow f\keq g$(Mather-Yauの定理)
を用います.数式処理ソフトSingularで$T(g_{1}),T(g_{2}),T(g_{3})$を調べると生成元を見比べれば,すぐに確認できます.手計算はやめとけ.

それぞれのTjurina数を求めると,$\tau(g_{1})=16$,$\tau(g_{2})=17$,$\tau(g_{3})=18$になります.
齋藤の定理から,$\tau(f)=18$の時のみ重み付き斉次多項式$g_{3}=x^{3}+y^{10}$に$\R,\K$-同値です.　ヤバ！！(ギャルピース)
また,$f_{a,b}$は$a,b$についてモジュライ($\R$-同値について)です。すなわち,$f_{a,b}\req f_{c,d}$ならば$(a,b)=(c,d)$ということです.これを考えれば「$\K$-同値だけど$\R$-同値でない」関数の具体例も得られますね！！ワオ！！

まとめ

• 単純特異点を勉強しよう
• 有限決定性を勉強しよう
• 齋藤の定理は大事
• 坂東は英二
• Mather-Yauの定理〜名前だけでも覚えて帰ってください

以上しんぎゅらでした！！まったね〜〜！！