円を拡張（?）した曲線たちについて［知見なし］
はじめに
将来的に調べてみたいと思っていたテーマですが、学力が低すぎてキッカケすらつかめないので、
ネットの海に放流しておこうと思います。この記事に数学的な知見は何もありません。
動機
「三角関数に類似した別の関数を考えたら有用なのでは？」
おそらく、だれもが一度は考えるであろうこのテーマが出発点です。
三角関数は円から生まれるので、円の概念から派生した別の曲線を使って
同じような関数を作る。というのが基本的な方針。
曲線のはなし
定点$\mathrm{A}$がある. ある点$\mathrm{P}$に対し
$$\mathrm{AP}=d$$
とする. $c$を定数として
$$d=c$$
を満たす点$\mathrm{P}$の集合を円とよぶ.
定点$\mathrm{A}_1$, $\mathrm{A}_2$がある. ある点$\mathrm{P}$に対し
$\mathrm{A}_1\mathrm{P}=d_1$,$\mathrm{A}_2\mathrm{P}=d_2$
とする. $c$を定数として
$$d_1+d_2=c$$
を満たす点$\mathrm{P}$の集合を楕円とよぶ.
これを参考にして拡げてみれば良いよね。ということで
$n$個の点$\mathrm{A}_{1}$,$\mathrm{A}_{2}$,$\mathrm{A}_{3}$,$\cdots$,$\mathrm{A}_{n}$がある. ある点$\mathrm{P}$に対し
$\mathrm{A}_k\mathrm{P}=d_k$
とする.
$d_{1}$,$d_{2}$,$d_{3}$,$\cdots$,$d_{n}$を組み合わせて四則演算したものを
$$L(d_{1},d_{2},d_{3},\ldots,d_{n})$$
とおく. $c$を定数として
$$L(d_{1},d_{2},d_{3},\ldots,d_{n})=c$$
を満たす点$\mathrm{P}$の集合を円派生曲線とよぶ.
$L$については
- 和
- 基本対称式
など色々な式を考えてみる。
と、結構大きく風呂敷を拡げた結果……
……
何の成果も得られませんでした。
もう、学力が低すぎてどこから手を付けたら良いのかすら分からない。
曲線の描画
とりあえず、曲線の形を知りたかったので描画してみました。
参考までに、「3点からの距離の和が一定の曲線」の描き方を置いておきます。
- GeoGebrageogを立ち上げて適当に3点A、B、Cを置きます。
- 数式として「sqrt((x-x(A))^2+(y-y(A))^2)+sqrt((x-x(B))^2+(y-y(B))^2)+sqrt((x-x(C))^2+(y-y(C))^2)=L0」
を入力します。 - L0のスライダーの設定を0～100くらいにします
- 点やスライダーをぐりぐり動かします。はい、面白い。
ちなみに、入力コマンドだと読みにくいので数式で書くとこんな感じ
$$\sqrt{(x-x_{A})^{2}+(y-y_{A})^{2}}+\sqrt{(x-x_{B})^{2}+(y-y_{B})^{2}}
+\sqrt{(x-x_{C})^{2}+(y-y_{C})^{2}}=L_{0}$$
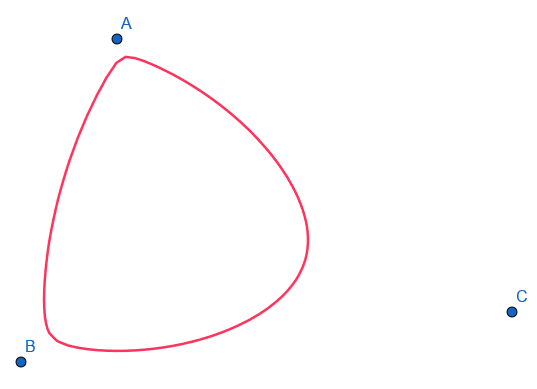3点からの距離の和が一定の曲線
おわりに
この種の関数を描画してグリグリ動かしてみると、見方によっては液体みたいな動きにも見えてくるので面白いですよ。
遠い未来に、頭の良い人がこの曲線群について調べてくれて、
私にもわかる形で発表してくださることを祈ってこの記事を閉じることにします。
ここまで読んでいただきありがとうございました。
