清里C
夏季セミナーの住所録に放流した問題になります.
正方形からなるマス目に対して,以下を満たす凸とは限らない多角形をループとします.
- 周が全てのマス目の中心を通る.
- 各辺は全てマス目の縦か横に平行である.
- 頂点は全てマス目の中心である.
- どの二辺も頂点以外の共有点を持たず,どの頂点もその点から出る辺は二本のみである.
- どの内角も$90$度か$270$度である.
シンプルループというパズルを考えていただけるとわかりやすいと思います.(というかそこから思いついた問題です)
ちゃんと定義出来てるか不安ですが不備あったら教えてくれると嬉しいです.
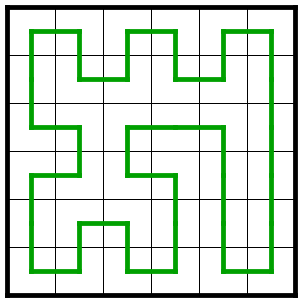 ループ例
ループ例
$n\times n$のマス目のループであって,全ての辺の長さが$2$以下であるようなものが存在するような正整数$n$を全て求めよ.
$n$は偶数である.
マス目を市松模様で白黒に塗り分ける.多角形の周は白,黒,白,$\cdots$の順番で通るので,白の数と黒の数は同じである必要がある.
しかし$n$が奇数の時マス目の数が奇数なので白の数と黒の数は同じにならない.したがって$n$は偶数である.
 奇数の市松模様
奇数の市松模様
$n$が$8$以上の偶数なら条件を満たすループが存在する.
以下の三つを組み合わせていく.
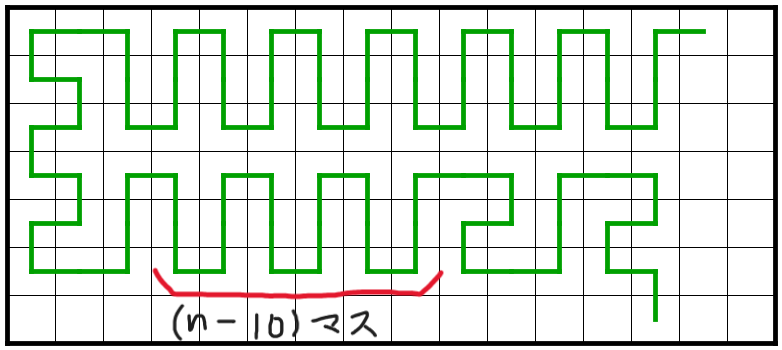 a
a
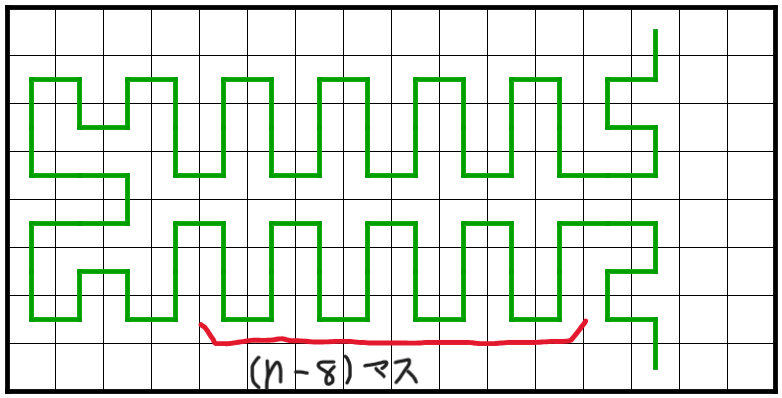 b
b
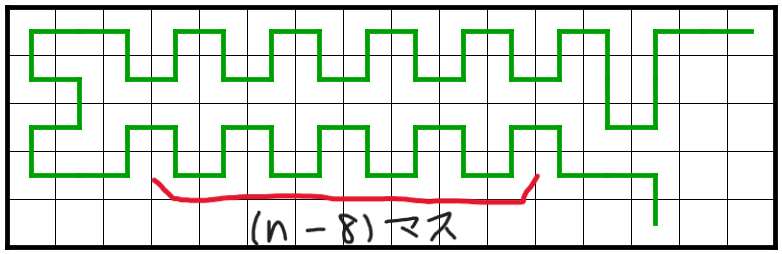 c
c
aとcを上下反転したものをそれぞれa',c'とする.
右側の幅二マスの行は匚の形を組み合わせていけばうまいこと埋まることが分かる.左側の幅$n-2$マスの行は,
- $n$が$6$の倍数なら上からa,$\frac{n-12}{6}$個のb,a'
- $n$が$6$で割って$2$余るなら上からc,$\frac{n-8}{6}$個のb,c'
- $n$が$6$で割って$4$余るなら上からa,$\frac{n-10}{6}$個のb,c'
とすれば埋まる.
![!FORMULA[23][1134102610][0]における例](https://firebasestorage.googleapis.com/v0/b/mathlog-361213.appspot.com/o/uploads%2Fmathdown%2FeChPsYH86xOSespHsN1u.png?alt=media) $n=10$における例
$n=10$における例
後は$n=2,4,6$を確かめるのみとなった.
$n=4$のとき条件を満たすループは存在しない.
上から$i$マス目,左から$j$マス目のマスの中心を$A_{i,j}$とする.
$A_{1,1}$は角なので,線分$A_{1,2}A_{1,1}$と$A_{2,1}A_{1,1}$を通る辺がそれぞれ存在する.$A_{1,2}$と$A_{2,1}$の両方に頂点があった場合,それぞれの点で曲がった辺はどちらも$A_{2,2}$を通るためループにならない.
したがって少なくともどちらかは頂点でない.対称性より$A_{2,1}$が頂点でないとしていいのでそのようにする.このとき線分$A_{1,1}A_{3,1}$を含む辺が存在する.
$A_{4,1}$は角なので,線分$A_{4,1}A_{3,1}$を含む辺が存在する.そのため,線分$A_{1,1}A_{4,1}$を含む辺が存在するが,この長さは$3$以上となってしまう.
したがって$n=4$のとき条件を満たすループは存在しない.
あとは$n=2,6$の場合だが,実際やってみれば難しくなく構成できるので,$n$は$4$以外の偶数とわかる.
さいごに
図を出すのが面倒くさかったのでできるだけ言語で何とかしようとしたが,結構分かりにくい文章になってしまった気がする.
問題はメインパートが構成であるというギャグ.構成例もこれ以外の方法を教えてくれた方もいる.偶数から4を省きたいという人はぜひ使ってください.
今回は初めて書く記事となった.今後使っていって慣れていきたいと思っている.まずは最初の方みたいな正方形や縦長の画像をもう少し小さく表示する方法から身に着けたいと思う.
