伊原ゼータ関数入門1
今回の記事では伊原ゼータ関数の定義を紹介します.
基本的なグラフ理論の用語
グラフ$G$とは集合$V(G)$と族(同じものを含む集合)$E(G)$の対$(V(G),E(G))$のことである.
$V(G)$とは点(節点,頂点)と呼ばれる元の非空な有限集合である.
$E(G)$とは$V(G)$ の異なる2点の非順序対を元(この元は辺と呼ばれる)とする有限な族である。
$V(G)$を$G$の点集合, $E(G)$を$G$の辺集合という.
 グラフ
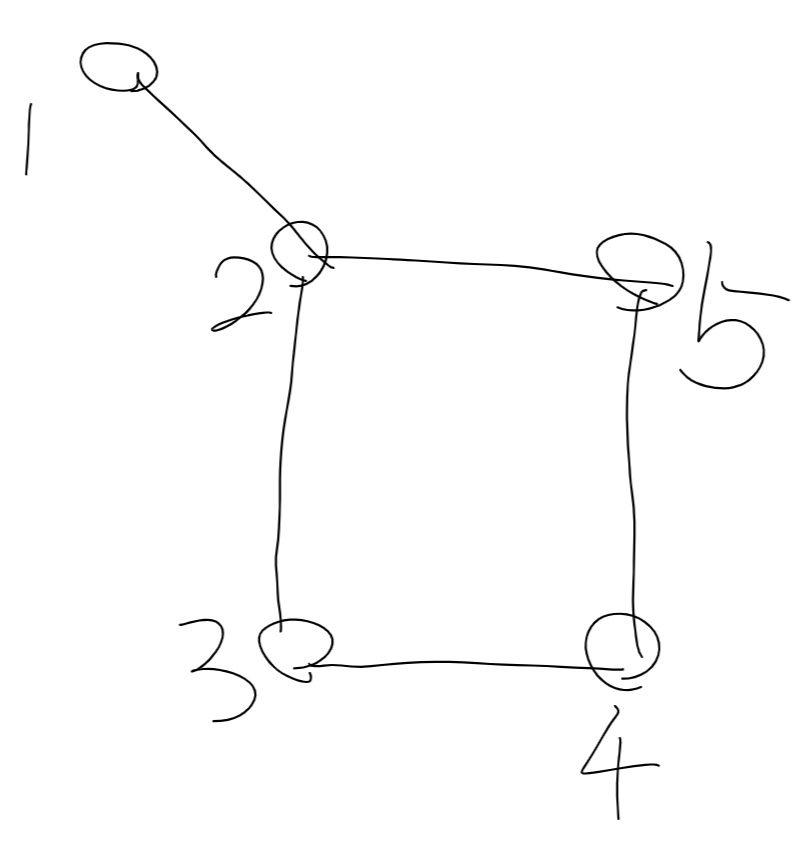
グラフ
図1のグラフの点集合は{1,2,3,4,5}であり, 辺集合は{{1,2},{2,3},{3,4},{5,4},{2,5}}であることがわかる.
有向グラフDとは集合$V(D)$と族(同じものを含む集合)$E(D)$の対$(V(D),E(D))$のことである.
弧$V(D)$とは点(節点,頂点)と呼ばれる元の非空な有限集合である.
$E(D)$とは$V(D)$ の異なる2点の順序対を元(この元は弧と呼ばれる)とする有限な族である。
弧の第一成分が$u$,第二成分が$v$であるとき,$u$から$v$への弧と呼ばれ,$(u,v)$または$uv$と書かれる.
 有向グラフ
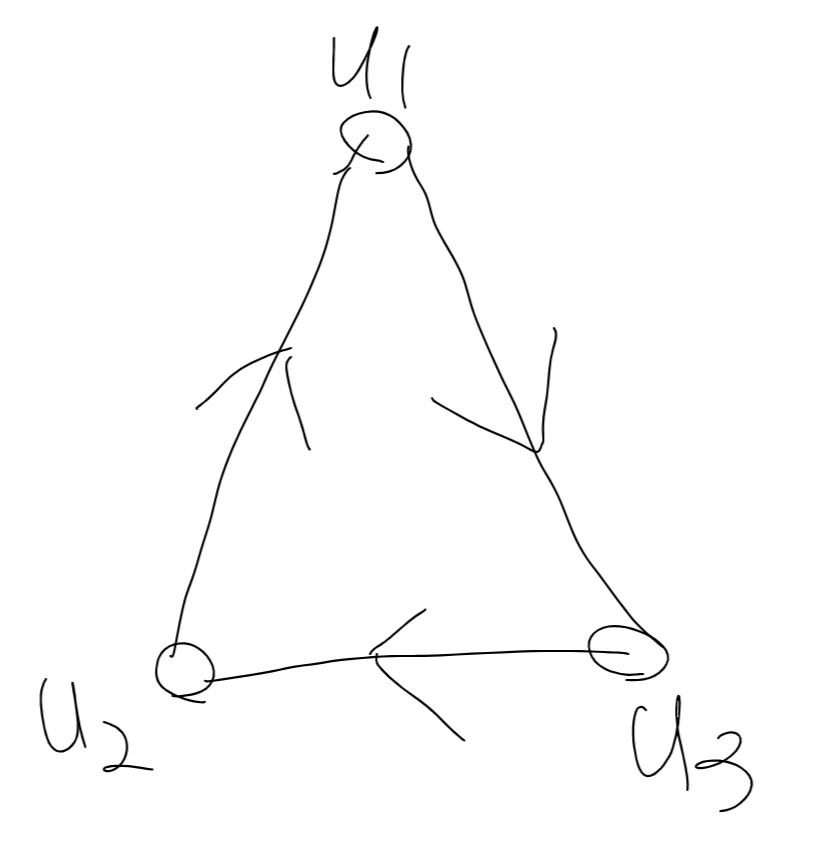
有向グラフ
図2のグラフの点集合は{$u_1$,$u_2$,$u_3$}であり, 弧の集合は{($u_2$,$u_1$),($u_3$,$u_2$),($u_1$,$u_3$)}であることがわかる.
グラフ$G$に対して,$G$のpath$P$とは$v_0v_1$,$v_1v_2$,$\cdots$ ,$v_{m-1} v_m$という形をした辺の有限列のことであり,$a_i$=($ v_{i-1},v_i $)($i$$\in${1,2,$\cdots$,$m$})としたとき,$P$=$a_1$$a_2$$\cdots$$a_m$と表すこともある.
$v_0$をそのpathの始点,$v_m$をそのpathの終点と呼ぶ.
$G$のpathの長さとはpathに含まれている辺の個数である.
closed pathとは始点と終点が同じであるpathのことである.
グラフ$G$の任意の点$x$,$y$に対して,$x$から$y$へのpathが存在するとき,$G$は連結であるという.
伊原ゼータ関数の定義
以下,グラフは連結であることを仮定する.
path$P$=$a_1$$a_2$$\cdots$$a_m$がbacktracklessとは任意の$i$$\in${1,2,$\cdots$,$m$}に対して,$a_{i+1}$=$a_{i}^{-1}$($a_{i}^{-1}$=($v_i$,$v_{i-1}$))とならないことである.
path$P$がtaillessとは,P=$a_1$$a_2$$\cdots$$a_{1}^{-1}$という形をしていないことである.
path$P$=$a_1$$a_2$$\cdots$$a_m$の同値類[P]とは
[P]={$a_1$$a_2$$\cdots$$a_m$ ,$a_2$$a_3$$\cdots$$a_1$,$\cdots$,$a_m$$a_1$$\cdots$$a_{m-1}$ }
グラフ$G$のpath$P$がPrimitive pathであるとは, $P$=$D^{n}$($D$は$G$のclosed pathであり,$D$=$a_1$$a_2$$\cdots$$a_1$であるとき,$D^{n}$は$D$=$a_1$$a_2$$\cdots$$a_1$をn回渡ったもの)とならないことである.
$v(P)$をpath$P$の長さとする.
グラフ$G$の伊原ゼータ関数$\zeta$$(u,G)$とは
$\zeta$$(u,G)$=$\prod_{[P]primitive} $(1- $u^{v(p)}$ )$^{-1}$
($u \in \mathbb{C}$, $\left| u \right|$は十分小さい,$[P]$はbacktracklessでtaillessでclosedなprimitive pathの同値類 )
以上が伊原ゼータ関数の定義になります.
ご拝読ありがとうございました.