作図がむずい系の良問紹介(from Iran TST)
はじめに
Iran TSTのとある問題が(見た目も中身も)面白かったので紹介します.射影とか(船旅9章)の良い練習になると思うのでぜひ解いてみてください.MOHSは20~25程度だと思います.
本編
点$O$を中心とする円に内接する四角形$ABCD$について,直線$AD$と$BC$の交点を$E$とし,直線$AC$と$BD$の交点を$F$とする.ある$2$点$P,Q$について,$PQ$を直径とする円$\omega$が直線$AC$と$BD$に接し,$F$が三角形$EPQ$の垂心であるとき,$\omega$の中心は直線$OE$上にあることを示せ.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
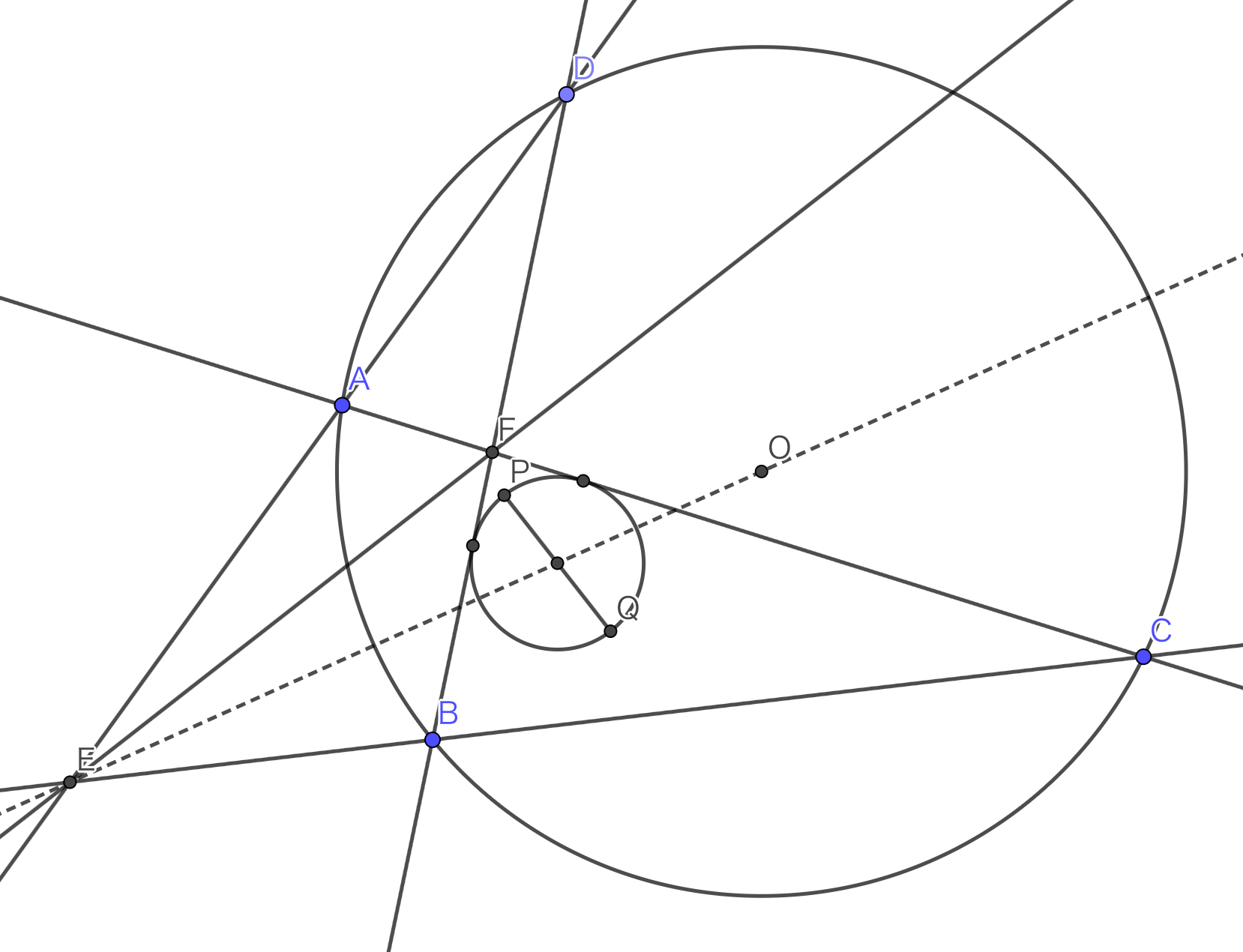 問題図
問題図
.
.
.
.
途中でも一応触れてはいますが位置関係の議論はガバガバです.あたたかくスルーしてください.
図の見た目がヤバいですね.$P$と$Q$がめっちゃ浮いてて気持ち悪い感じがします.とりあえず円$\omega$の中心を$N$とでもしておきましょう.
垂心の条件を言い換える
まず「$F$が$\triangle EPQ$の垂心である」というのを見やすくしておきましょう.まあ$PQ$が直径なので,「$EP\cap FQ$と$EQ\cap FP$がともに$\omega$上にある」ってのが分かりやすいですかね.前者を$S$,後者を$T$とでもしておきましょうか.
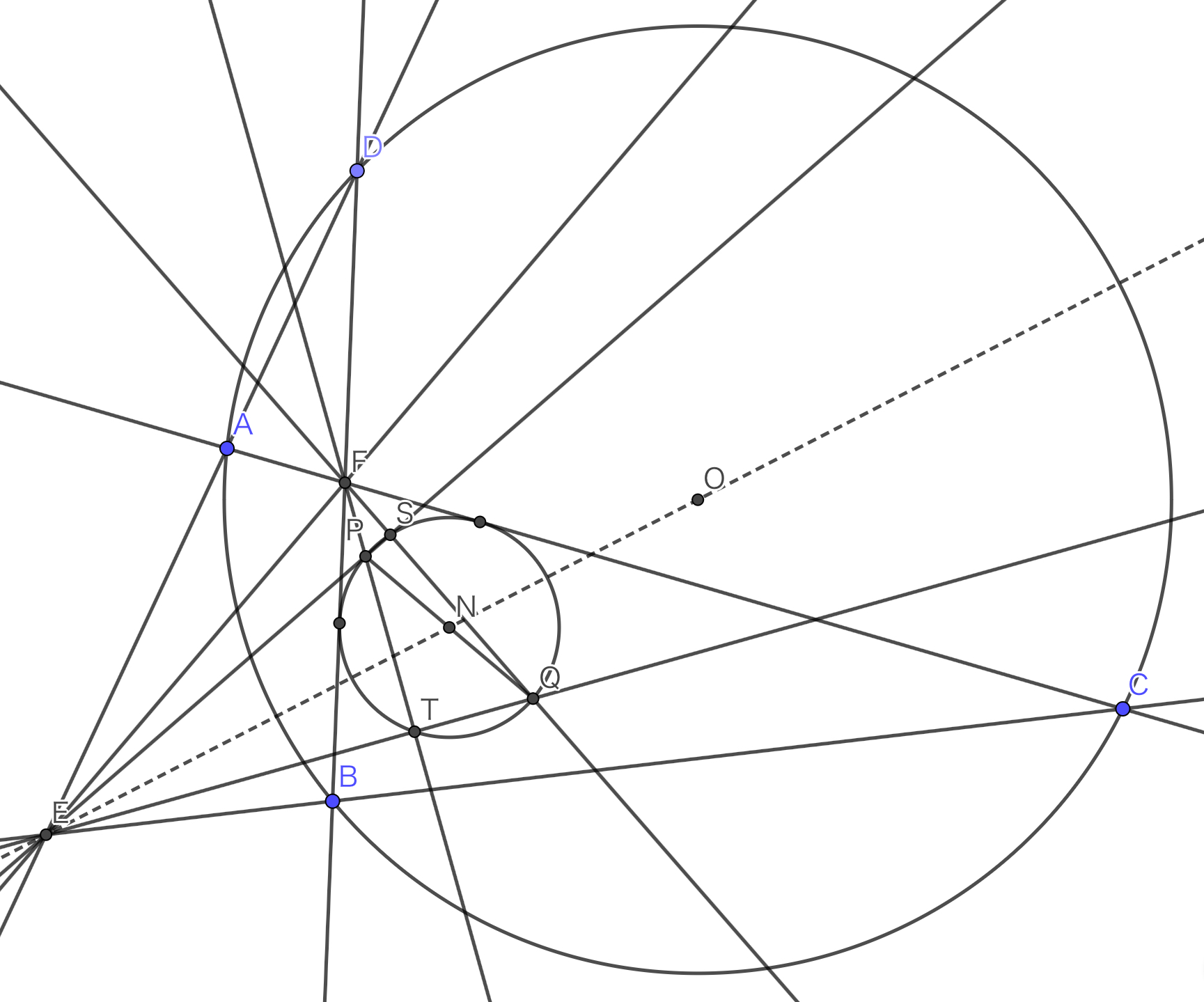 図です
図です
特に進捗はなさそうなので次に進みます.
円が接する条件を言い換える
$\omega$が$AC$と$BD$に接するってのも使いましょう.とりあえず$\omega$と$AC,BD$の接点をそれぞれ$X,Y$とします.
$\omega$がどっちの角の内部にあるかで図の形が大きく変わります.本当はちゃんとやらないとダメですが,今回は$\angle BFC$の内部にあるものとして扱います.
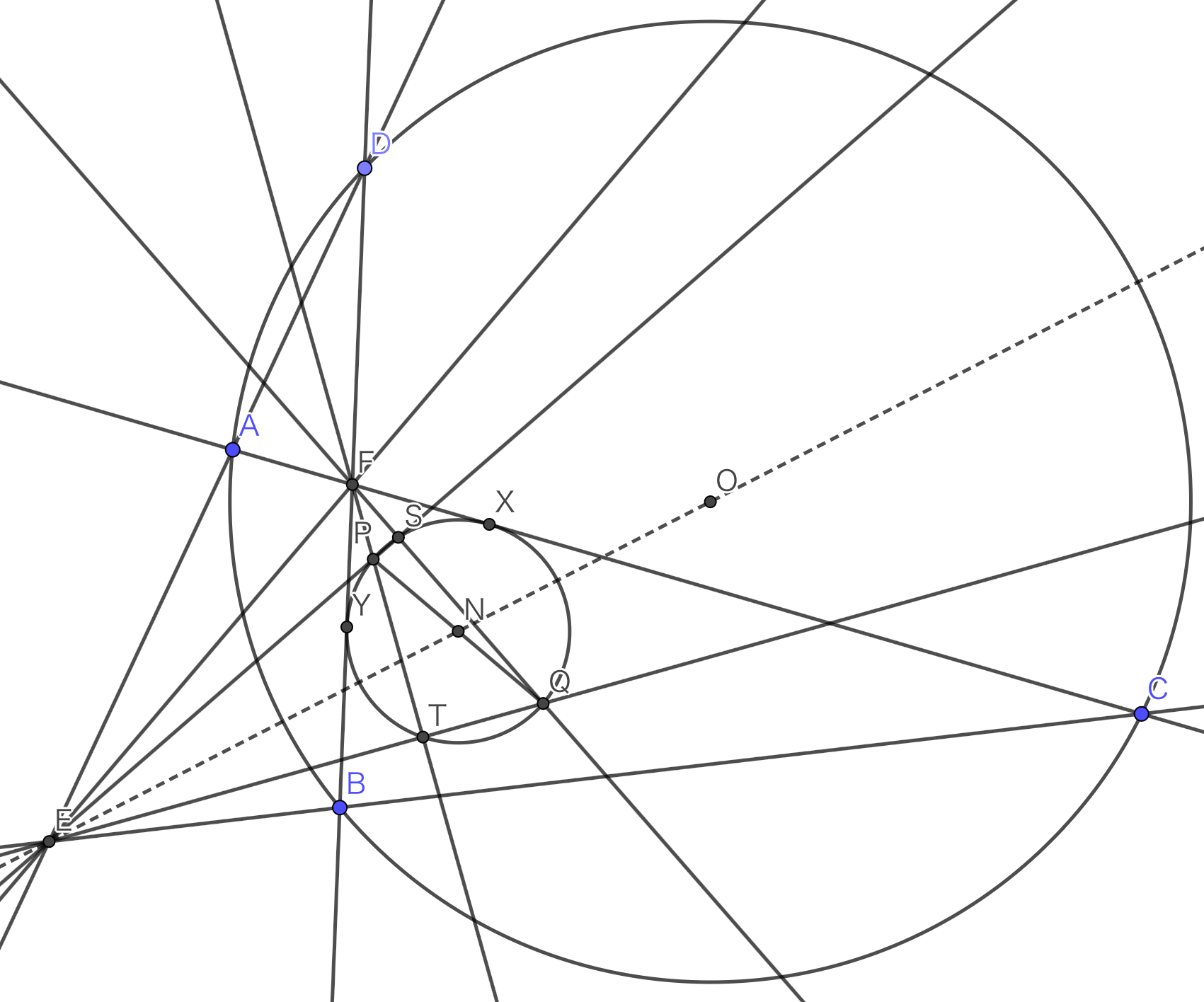 図です
図です
図を見るとなんかめっちゃ$E$が直線$XY$上にありそうな感じがします.これを示しましょう($\omega$周り以外の点は無視して良い).まあ完全四角形$PTQS$でBrocard使ってくれ〜みたいな見た目をしているのでそれを使えば良いです.実際,Brocardの定理から$E$は$F$の円$\omega$への極線上にあり,これは直線$XY$に他ならないのでOKですね.
こうなっちゃえばもう$\omega$とその周りの点は不要なので無視できます($FX=FY$だけが束縛条件として残る).消しちゃいましょう.
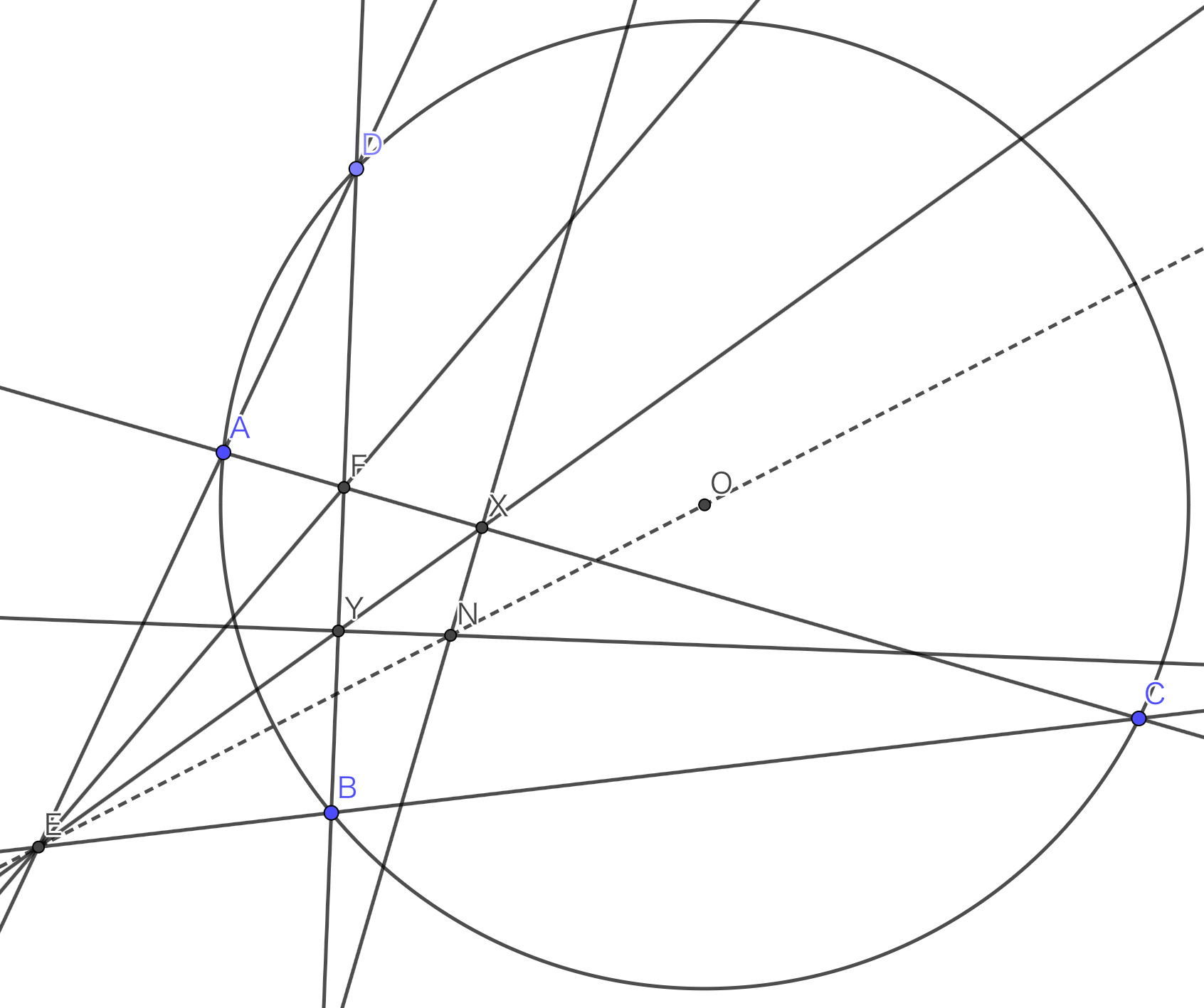 図です
図です
本質部分
だいぶ図がシンプルになりました.帰着後だ〜みたいな見た目をしていますね.$EX$が$\angle AEB$を二等分しそうな雰囲気がすごいので示しておきましょうか.(ちなみにこの後の議論では全く使いません,図も省略します)$XY\perp FN$なので,$FN$と$AB,AC$の交点を$K,L$として$EK=EL$であることを示せばいいですね.でもこれって割と自明で,$\triangle FAD$と$\triangle FBC$の相似で$K,L$が対応するので$\angle AKF=\angle BLF$であることから従います.めでたしめでたし.
二等分することを示せて気が楽になったところで本題の$E,N,O$の共線を示すことに戻りましょう.少し考えると分かりますが$N$が浮いててめっちゃ扱いづらいです.なので(次に書くことも含めて)一致法でいい感じに$N$を再定義する,みたいなノリで考えて行きたいですね.とりあえず$N$は見づらいので消しておきます.
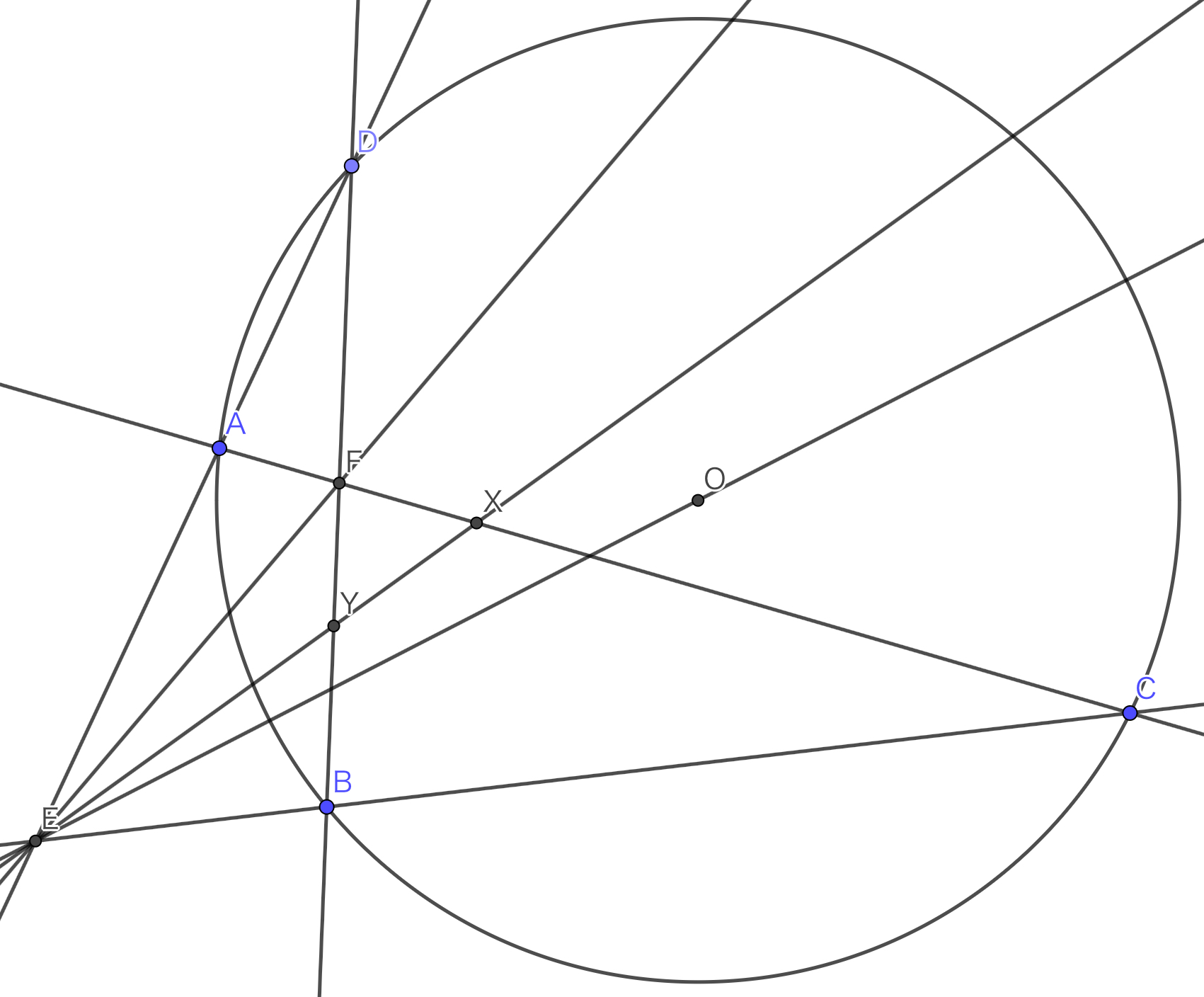 図です
図です
$E,F,O$があるので四角形$ABCD$にBrocardをしたいですね.$AB$と$CD$の交点を$G$とするとBrocardの定理より$FG\perp OE$です.ここでこれらの交点を$Z$とすると,$N$が$OE$上にあることと$F,X,Y,Z$の共円は同値であることが分かります!(円$FXYZ$に関する$F$の対蹠点を取って適当に一致法すれば良い)だいぶ見やすくなりましたね!
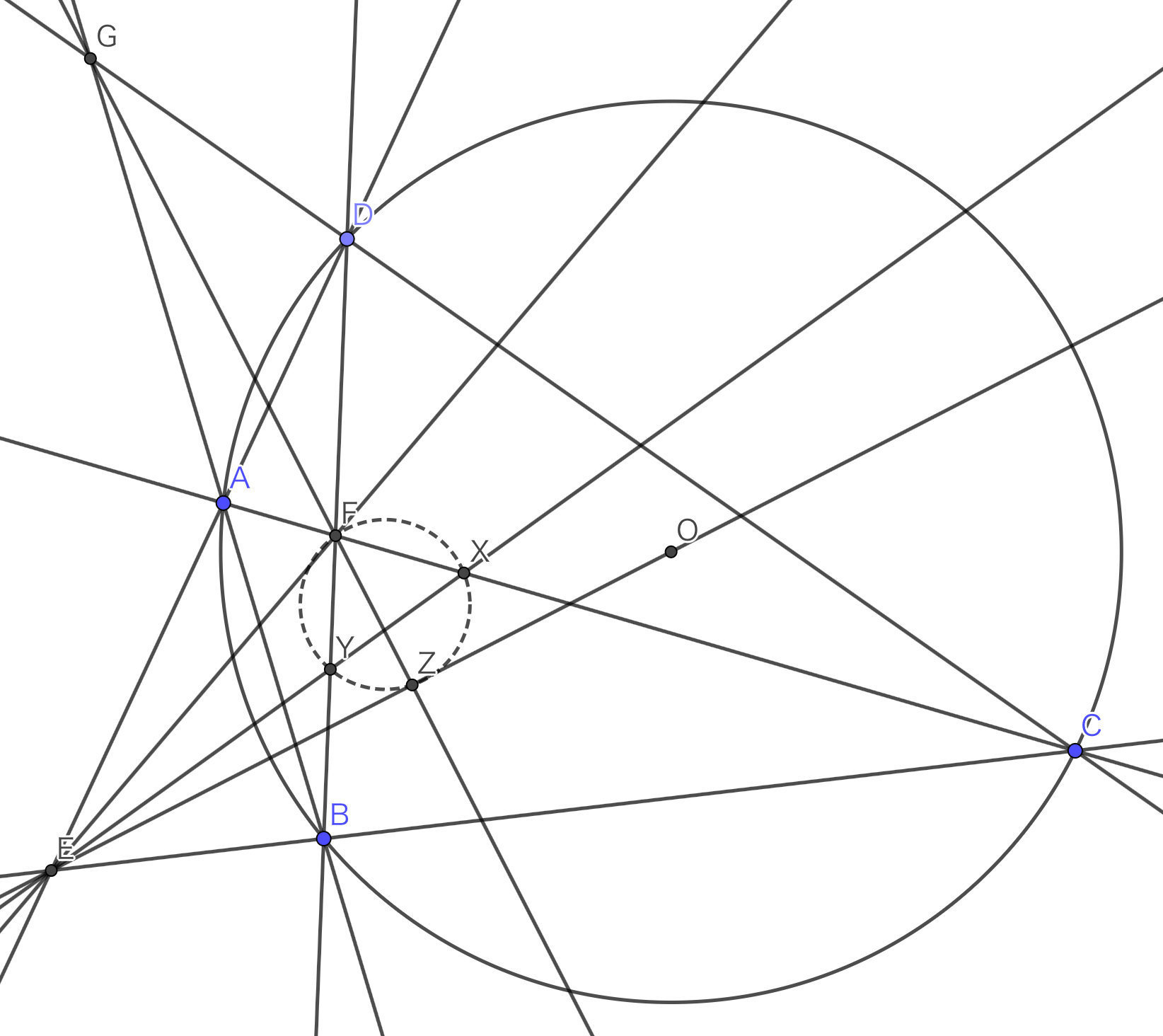 図です
図です
本当の本質部分
さて,$F,X,Y,Z$の共円を示します.$EX=EY$があるので$\angle EZX=\angle EZY$を示せば良いですね(これも$Z$が$XY$の垂直二等分線上にあるとバグりますがスルーします).$\angle FZE=90^\circ$に注意すると,(アポロニウスの円のアレ,船旅9.18から)$XY$と$FG$の交点を$W$として$X,Y;W,E$が調和点列であることを示せばいいと分かります.めっちゃ射影できそうな感じがするのでどんどんやっていきましょう!
まず$BC$と$FZ$の交点を$V$とすると$(X,Y;W,E)\overset{F}{=}(C,B;V,E)$ですね.ここで$(C,B;V,E)=-1$は,($\angle EZG=90^\circ$より)$FG$と円$ABCD$の交点を$I,J$として$IBJC$が調和四角形であることと同値です.すなわち$EI,EJ$が円$ABCD$に接することを示せばいいです.でもこれはBrocardの定理から$IJ$が$E$の円$ABCD$に関する極線であることから従います!!おわり!!
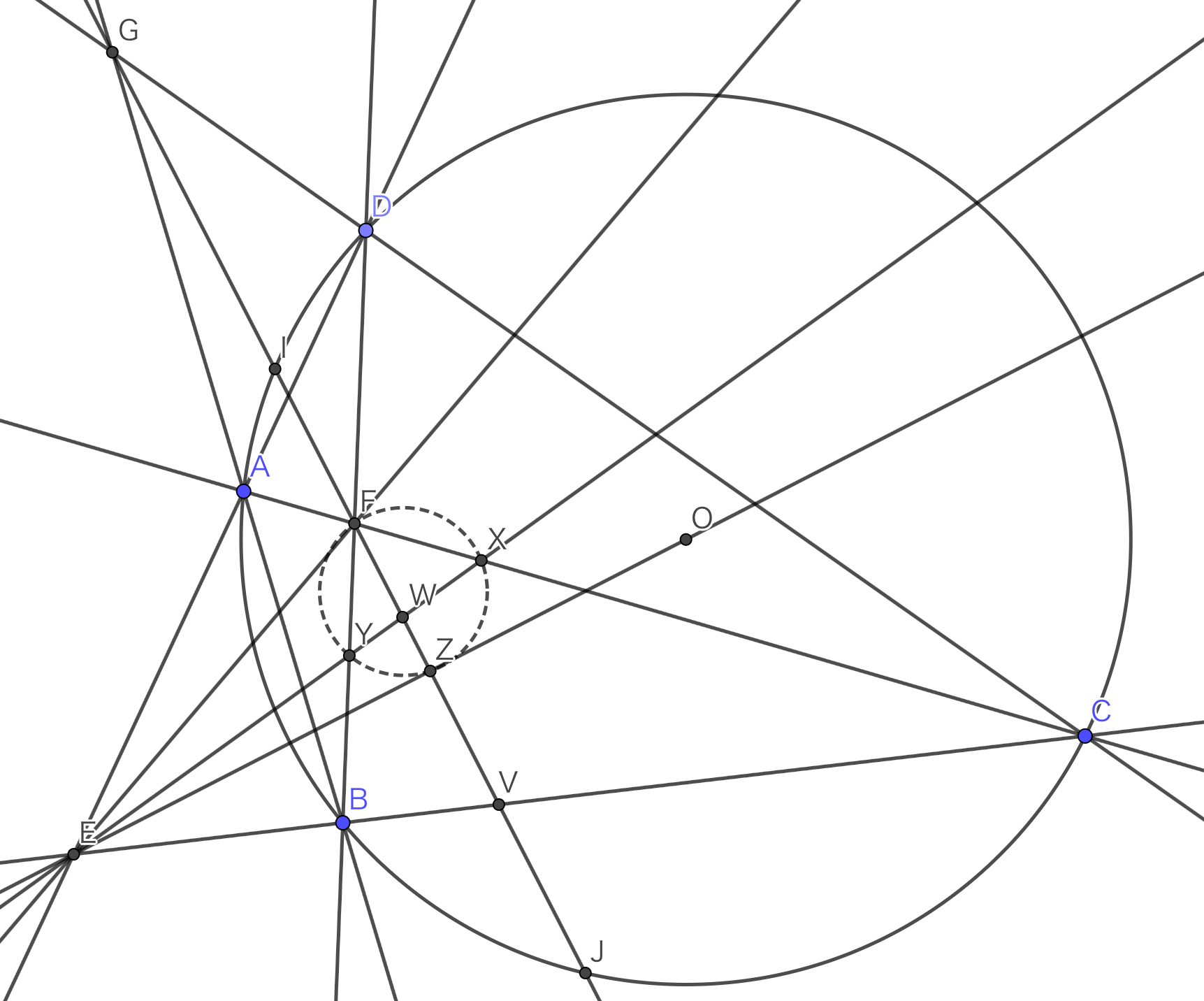 ラスト図です
ラスト図です 疲れた
おわりに
いかがでしたか?
