LGC short 問題解説・作問の背景について

初等幾何

　8/22に開催された求値幾何コンテスト「LGC short」についてです．解説だけでなく，その問題を作る際の背景についても書いていきます．(時々変な日本語が挟まる可能性があります)

p1．

　問題は以下の通りでした．

　$BC=8$なる三角形$ABC$において，内接円の半径は$2$，角$A$内の傍接円の半径は$5$であった．このとき，三角形$ABC$の面積を求めよ．

$BC$の長さがわかっているので，内接円半径と傍接円半径から高さを求めるのが自然な発想かと思います．そうなると，船旅に載っている有名な構図が使えます．

(船旅4.14)

　三角形$ABC$において，内心，角$A$内の傍心をそれぞれ$I,I_A$とし，内接円と角$A$内の傍接円が線分$BC$に，それぞれ$D,X$で接しているとする．このとき，直線$IX$と直線$I_AD$は$A$から辺$BC$に下ろした垂線の中点で交わる．

あとはこれを使って，垂線の長さと内接円半径，傍接円半径の比を考えれば終わりです．答えは$\dfrac{\textbf{80}}{\textbf3}$になります．

　この構図が個人的にかなり好きなので採用しました．僕にしては珍しく本当に短時間で作った問題で，p1をもうちょっと凝れたかな〜とも思ってました．

p2.

問題は以下の通りでした．

　三角形$ABC$において，内心を$I$，角$A$内の傍心を$I_A$，外心を$O$とすると，直線$II_A$と直線$IO$は垂直に交わった．線分$BC$の中点を$M$，線分$II_A$と線分$BC$の交点を$K$とし，三角形$MKI_A$の重心を$G$とすると，
$$KM=1，KG=3$$
が成立した．このとき，線分$BC$の長さを求めよ．

　この問題のコンセプトはずばり，$\angle AIO=90^\circ$は重心が熱い、です(実際はほとんど使わないで解けるのですが)．作問時はこのことを中心に作っていました．まず次のような性質が成り立ちます．特に書いてない点の定義は問題の通りです．

　三角形$ABC$の重心を$G^\prime$としたとき，$\angle AIO=90^\circ$ならば，$BC\parallel IG^\prime$である．

　$AI:IK=2:1$を示せば良い．三角形$ABC$の外接円の$A$を含まない方の弧$BC$の中点を$V$とすると，$AI=IV=VI_A$．また，方べきの定理から$AK\cdot KV=IK\cdot KI_A$なので，特に$IK=KV$．よって，$AI=2IK$なのでこの主張は示された．

これにより，$G^\prime,G,I_A$が同一直線上にあることが$G^\prime$からの射影でわかり，四角形$G^\prime MGK$が平行四辺形であることがわかるので，$AM=9$が得られます．
　$\angle AIO=90^\circ$におけるもうひとつの重要な事実を示しておきます．

　$\angle AIO=90^\circ$のとき，$AB:BK=AC:CK=2:1$である．

　方べきの定理より$AI\cdot AI_A=AB\cdot AC$であるので，特に$3AI^2=AB\cdot AC$．また方べきの定理より，$$BK\cdot CK=AK\cdot KV=\dfrac 34AI^2=\dfrac 14AB\cdot AC$$$AB:BK=AC:CK$は明らかなので，$BK=\dfrac 12AB,CK=\dfrac 12AC$が従い，この主張は示された．

　求める値を$x$と置くと，$AB< AC$のとき(対称なのでこのように仮定しても問題ない)，$AB=x-2,AC=x+2$です．あとは中線定理から$x$を計算することができ，$x=\sqrt{\dfrac{\textbf{308}}{\textbf{3}}}$が求められます．

　この解法では射影を用いてますが使わなくてもできます．(こっちの方がおそらく普通)
　線分$MI_A$の中点を$N$とすると，$KN=\dfrac 92$．いま，命題2の証明と同様に考えることで$AK=KI_A$であるので，中点連結定理より$AM=9$がわかり，あとは同様に計算するだけです．

　さて，今回のコンセプトが$\angle AIO=90^\circ$は重心が熱いということで$\angle AIO=90^\circ$のときに成り立つ重心関連の構図をもう一つ紹介します．解説には関係ないので証明は省略します．

　内接円と線分$BC$の接点を$D$とし，$I$について$D$と対称な点を$E$とする．このとき，$V,G^\prime,E$は共線である．

　$\angle AIO=90^\circ$という割とよくある条件を使った問題は僕にしては珍しかったかもしれません．ただ，重心系を絡めた問題はあまり見ないと思ったので今回作ってみました．が，問題文には絶対に三角形$ABC$の重心を入れたくないと拘った結果あまり重心を絡められず…もっと作問力を上げていきたいです．

p3．

　最終問題です．問題は以下の通りでした．

　鋭角三角形$ABC$において，$B$を通り直線$AC$に平行な直線上に点$P$を，$C$を通り直線$AB$に平行な直線上に点$Q$をそれぞれとると，$A,P,Q$はすべて直線$BC$に関して同じ方にあり，$\angle APB=\angle AQC$が成立した．また，三角形$PAB$の外接円と三角形$QAC$の外接円が再び交わる点を$X$とし，直線$PQ$と直線$BX,CX$が再び交わる点をそれぞれ$R,S$とすると，
$$\cos\angle BXC=\frac 15，CX-BX=5，XR:XS=5:3$$
が成立した．さらに，線分$BC$の中点を$M$，直線$AX$と三角形$PXQ$の外接円が再び交わる点を$T$とし，三角形$TPQ$の内心を$I$とすると，直線$AX$と直線$MI$は平行であった．このとき，線分$XI$の長さを求めよ．

　問題文が長い(当社比)！まず図を書きましょう．
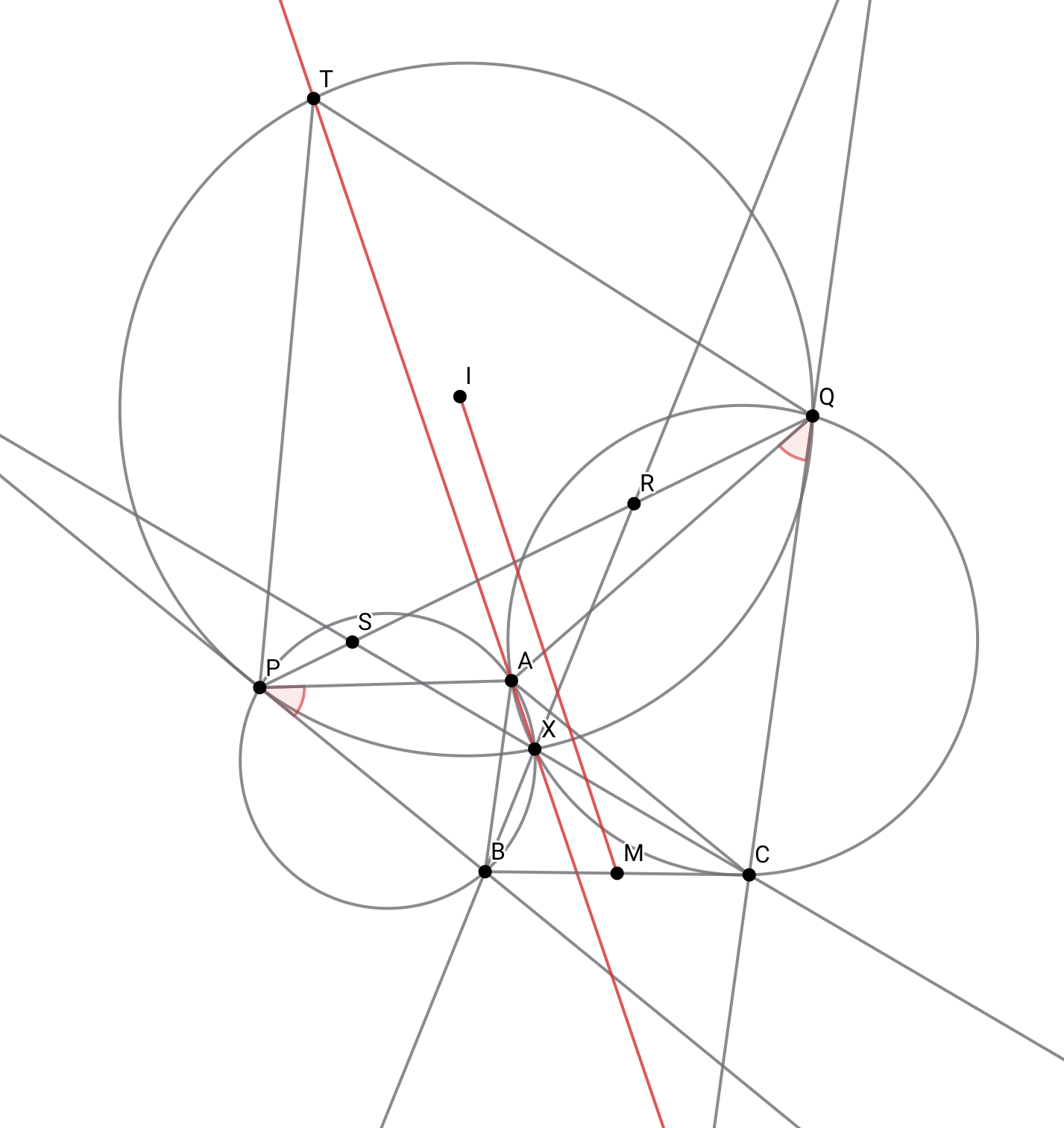ほう
$PB$と$QC$の交点は偉そうです．$M$について$A$と対称な点でもあるので．この点を$A^\prime$としましょう．

　はじめにすぐわかるのが三角形$APB$と三角形$AQC$の相似です．この相似からまず長さに注目すると，$AB\cdot CQ=AC\cdot BP$が得られます．いま，四角形$ABA^\prime C$は平行四辺形なので，これは$A^\prime C\cdot CQ=A^\prime B\cdot BP$に言い換えられ，つまり円$A^\prime PQ$に関して$B$の方べきと$C$の方べきが等しいということが言えます．よって，三角形$A^\prime PQ$の外心を$O$とすると，$OB=OC$が得られます．
　次に角度に注目します．すると，次の事実が得られます．証明は全て簡単なangle-chaseです．

　$\angle PXA=\angle QXA=\angle BA^\prime C$である．

　直線$AX$は$\angle BXC$の二等分線である．

さて，命題5から実は三角形$TPQ$は二等辺三角形だったことがわかります．さらに得られるのが次の事実です．

　$O$は円$XPQ$上にあり，$I$は円$A^\prime PQ$の$A^\prime$を含まない方の弧$PQ$の中点である．

この証明も簡単なangle-chaseになります．

　ところで図を描いてみても分かると思うのですが，とても$OXBC$が共円そうという感覚があります．ということでこれを証明していきます．(作問している最初の方はどうせ共円だろうくらいにしか思ってなかったのですが，思ったよりは証明は簡単ではないです)

　$O,X,B,C$は共円である．

　$Y$が円$A^\prime PQ$による反転でうつる先を$Y^*$と表す．このとき，$X^*,B^*,C^*$が共線であることを示せば良い．
　三角形$PAB$と三角形$QAC$の相似比を$1:k$とすると，$$PA^*:QA^*=\dfrac{OP}{OA}\cdot PA:\dfrac{OQ}{OA}\cdot QA=PA:QA=1:k$$$$A^*B^*:A^*C^*=\dfrac{OA^*}{OB}\cdot AB:\dfrac{OA^*}{OC}\cdot AC=AB:AC=1:k$$$$B^*P:C^*Q=\dfrac{OP}{OB}\cdot BP:\dfrac{OQ}{OC}\cdot CQ=BP:CQ=1:k$$よって，三角形$PA^*B^*$と三角形$QA^*C^*$は相似である．したがって，$\angle PA^*B^*=\angle QA^*C^*$．命題7より$X^*,P,Q$は共線なので，$$\angle PX^*B^*=\angle PA^*B^*=\angle QA^*C^*=\angle QX^*C^*=\angle PX^*C^*$$よって位置関係に注意すると$X^*,B^*,C^*$は共線なので，この主張は示された．

(この書き方嘘すぎてヤバいな，あとで修正します)

　ここまでは$\angle APB=\angle AQC$から議論していましたが，別の条件も使っていきましょう．$XR:XS$ですが流石にこのままだと使いづらいです．そこでこの線分を伸ばしてみます．$BX,CX$が円$XPQ$と再び交わる点をそれぞれ$D,E$とすると，命題6が効いて$XR:XS=XD:XE$です．このとき，三角形$XBC$と三角形$XDE$についてある有名構図が使えます．
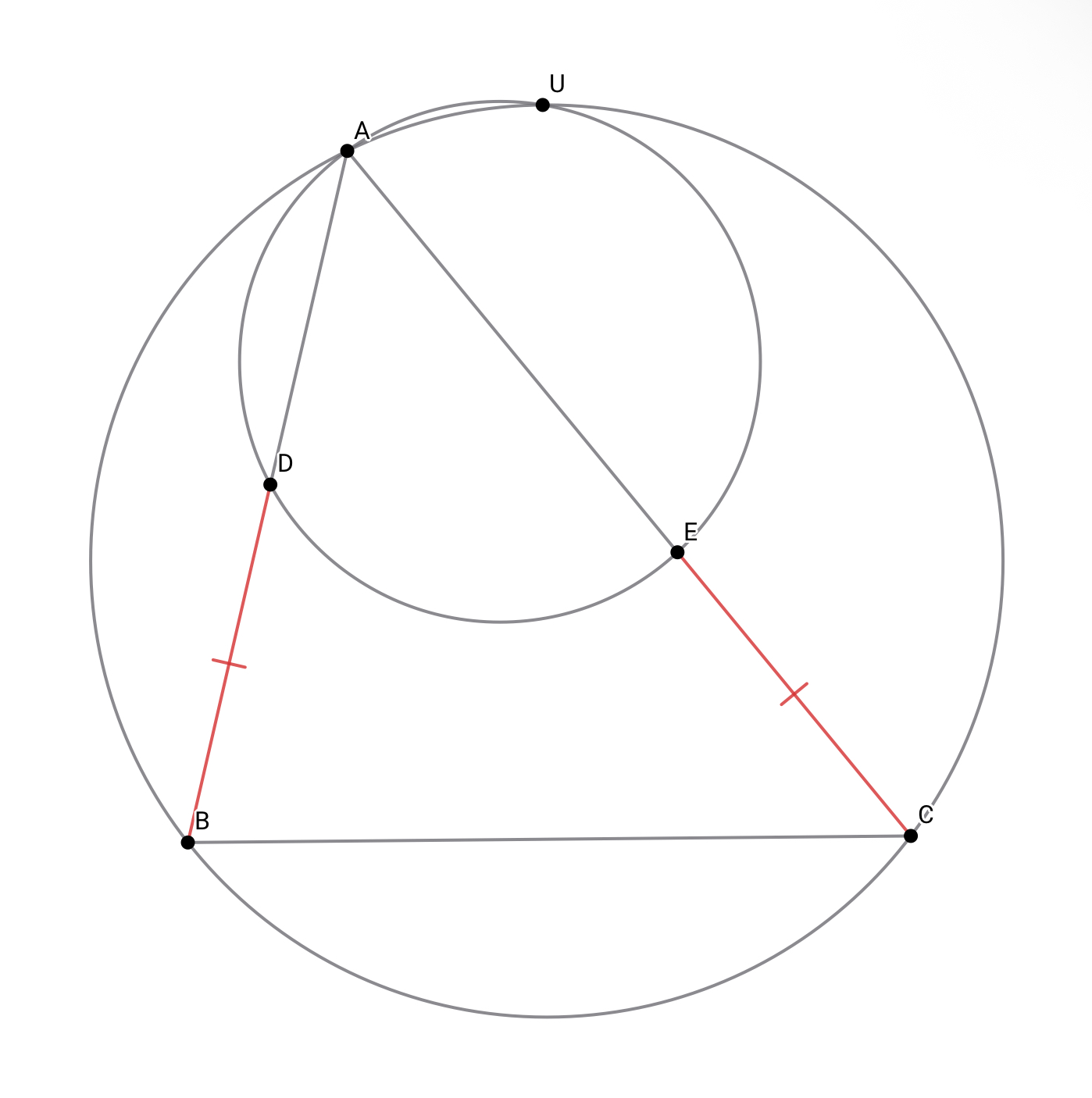これです
　つまり，$BD=CE$です．めっちゃ$CX-BX$と$XR:XS$が使えるようになってしまいました．計算すると$XD=\dfrac{25}{2},XE=\dfrac{15}{5}$が得られます．

　今度は$AX\parallel MI$を使っていきましょう．$M$を使わなければいけません．どう使うですが$DE$の中点を考えるとうまくいきます．この中点を$N$とすると，$\angle OMN=\angle OCB$からangle-chaseより$AX\parallel MN$がわかります．つまり$I=N$だったわけです．

　あとは計算するだけです．$\cos$がわかっているので$DE$を計算でき，中線定理によって$XI=\sqrt{\dfrac{\textbf{125}}{\textbf{2}}}$が計算できます．

　初めて高難易度幾何を作りました．自由度が足りなくて長さ系の条件が全部かなり変になってしまいましたが，それもそれで良かったかもしれません．(ただやっぱりもうちょっといい条件があったかな…)僕は基本的に長さの条件を考えるのに一番時間を使っていて，今回もかなり時間がかかりました．ただ求値幾何では，どれだけ構図が良くても計算が重すぎると結局不快な問題になってしまうのでこれは結構大事だと思います．もう一つ数値設定で気をつけてることがあって，それはその構図を活かし切ることです．やっぱりそうじゃないと勿体無いので．
　この問題を作る際のコンセプトは「方べきが等しい→$O$からの距離が等しい」でした．それを平行四辺形を使うことで上手い条件にできました．元々は三角形があって内部に点があって平行四辺形があるよ〜みたいな感じの問題文にしようと思ってましたが，平行四辺形基準にしようとなり，冷静に1点いらないなというふうになって行きました．問題文の点は減らせば減らすだけ良いのです．