"the hat" が平面を非周期的にしかタイリングできないことの証明

はじめに
§1§　準備と観察
§2§　正三角形格子の性質
§3§　証明の方針
§4§　証明の核心
仮定
相似にはならない
相似になる
矛盾、そして背理法の完成
おまけ1　the hat には「1方向のみの並進対称性」もない
おまけ2　Spectre について
おまけ3　論文を読んでみよう
論文中の専門用語
おわりに
参考文献

高校数学解説

文献あり

"the hat" が平面を非周期的にしかタイリングできないことの証明

日曜数学会,the hat,非周期的タイリング

1392

はじめに

hat tiling

※　この記事の内容の簡略版は、第27回日曜数学会　で発表しましたのであわせてご覧ください。

今日の #日曜数学会での発表資料をぶら下げます。

the hat が非周期モノタイルである事の証明
1～4/n pic.twitter.com/8Z8PEsVRCm
— ａｐｕ (@apu_yokai) June 25, 2023

　2023年3月20日に発表された、 "the hat" と名付けられた図形についての論文は、界隈に衝撃を持って迎えられました。

　タイリング界隈の未解決問題、「アインシュタイン問題」がついに解決したというのです!

　「アインシュタイン問題」というのは一言でいうと「非周期的にしか平面を敷き詰められないような図形の組合せのうち、図形の種類が１種類だけのものは存在するか」というものです。

　非周期的タイリングといえばペンローズのタイルが知られていますが、ペンローズのタイルには２種類のタイルが必要です。また、ペンローズのタイリングに使われるひし形２種類のタイルの場合、ならべかたに制限を加えなければ周期的なタイリングも可能です。

ペンローズタイルをもとにした非周期敷き詰めの例

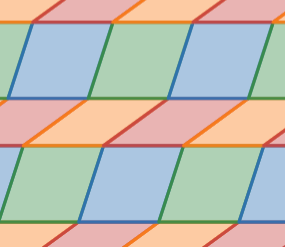ひし形のペンローズタイルは並べ方を制限しなければ周期的なタイリング可能

　実は今回発見された the hat は、１種類のタイルで非周期的にタイリングできるだけでなく、並べ方に制限を加えなくても、非周期的にしか平面全体を敷き詰められない、という驚くべき性質を持っていたのです!

　なお、「アインシュタイン問題」と呼ばれていますが、相対性理論で知られるアインシュタイン博士とは関係なくて、ドイツ語でアイン(Ein)が「一つの」、シュタイン(stein)が「石」という意味であることからこの名がつけられたようです。

　震源地となった"the hat" の論文はこちら(無料でダウンロードできます)
arxiv:An aperiodic monotile

　この記事では、the hat が平面を非周期的にしか敷き詰められないことを、ざっくりと証明します。

　この記事での証明の方針は論文に記載されていた証明方法をベースに、私なりの解釈を加えたものになります。もしヤバそうなところを見つけたら、こっそり教えてね(弱気)。

§1§　準備と観察

　では、今回発見された"the hat" の形状をよく観察してみましょう。

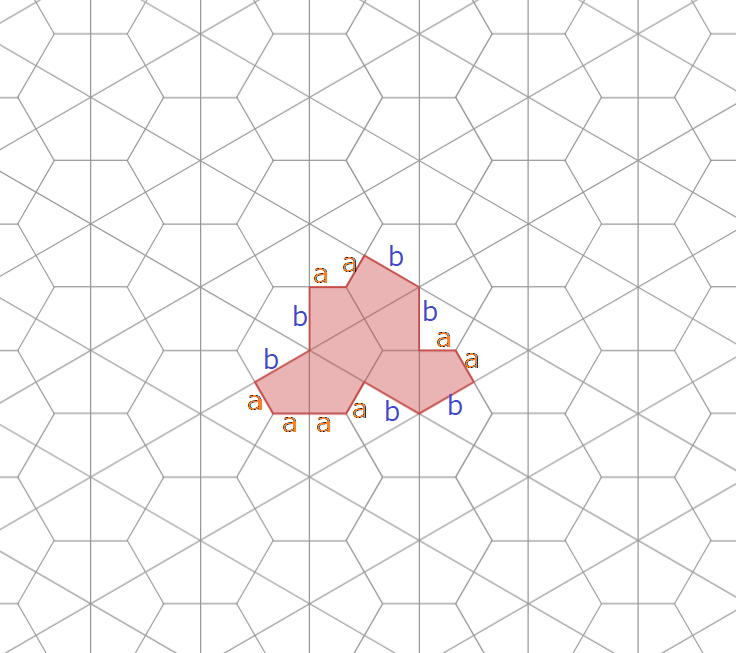the hat とベース格子

the hat の辺はすべて正三角形と正六角形を組み合わせたような格子上の線と重なっています。
この、正三角形と正六角形を組み合わせたような格子は論文中では "Laves tiling[3.4.6.4]" と呼ばれていますが、この記事では「ベース格子」と呼ぶことにします。

ここは読み飛ばしても良いです。

　the hat で平面全体のタイリングをするには必ずベース格子に重なるように配置しなければなりません。そのことをきちんと証明するのはちょっと面倒なのですが、次のように考えると直感的にわかります。

　まず、ベース格子に重なるように１枚タイルを貼ります。次に、タイルを１枚ずつ、「凹んだところに合わせて次のタイルを貼っていく」という操作を考えます。どんな風ににタイルを貼っていっても、the hat の形状から、必ず凹部ができます。凹部に新しいタイルを貼るときは、ベース格子と重なるようにしか貼ることはできません。

(論文では、補題A.6でちゃんと証明されています。)

　ベース格子の単位辺の長さは $2$ 種類あり、その長さの比が $1 : \sqrt{3}$ となっていることに注目してください。

　実は、"the hat" の辺の長さを二つの変数 $a, b$ で表して、 $a, b$ を動かしてタイルの形を変形(角度はそのままで辺の長さだけ変える)しても、同じ配置でタイリングすることができます。

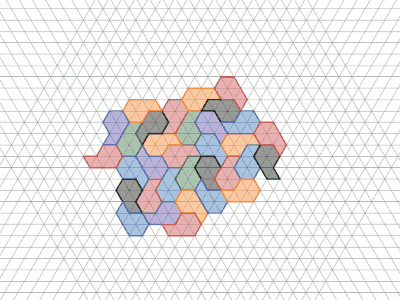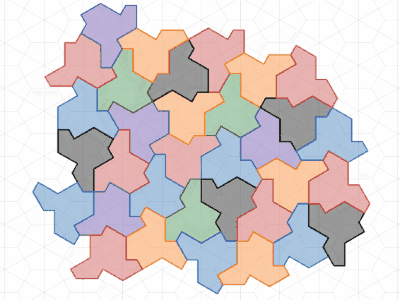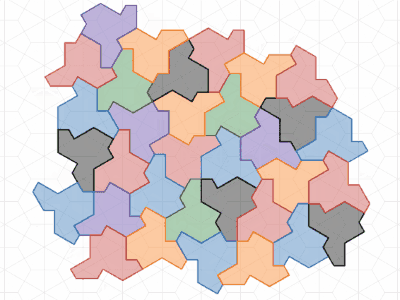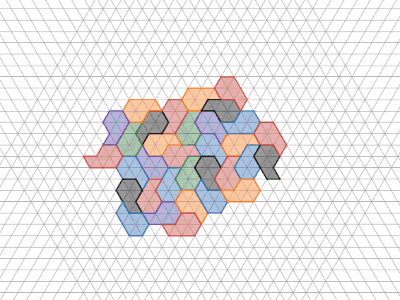辺の長さを変化させてもタイリングできる

　元の論文では、 $Tile (a, b)$ としてこれらのタイルを表しています。

　(2023.7.1追記)
　なぜこのような変形ができるのか考えてみましょう。
【１枚のタイルについて連続的に変形できる理由】
辺の長さで分ける

　the hat の長さ $a$ の辺だけ、長さ $b$ の辺だけをそれぞれ平行移動して組み合わせて多角形をつくることができます。それぞれの多角形の辺をベクトルで考えると、その和はどちらもゼロベクトルですから、それらを組み合わせた　the hat の辺をベクトルで考えたものの和もゼロベクトルです。
　したがって、 $a, b$ を動かして破綻することなくタイルの形を変形することができます。

【タイリングについて連続的に変形できる理由】
　タイリングの各頂点回りのタイルに注目します。頂点回りのタイルは、 $a, b$ が変化しても、その組み合わせは変化しません。
　次にタイリングの各辺に注目します。ここで「タイリングの各辺」とは、「個々のタイルの辺」とは異なる概念として考えてください。
　タイリングの各辺の長さもまた、 $a, b$ のどちらかになりますが、長さ $a$
の「タイリングの辺」の両側には、どちらも長さ $a$ の「個々のタイルの辺」が対応しています。 $a, b$ が変化しても、その組み合わせは変化しません。
　これらのことから、 $a, b$ が変化しても、個々のタイルの隣接関係が変化しないことがわかり、タイリング全体もまた連続的に変形できることがわかります。

論文より引用：いろいろな Tile(a,b) の例

"the hat" は $Tile (1, \sqrt{3})$ に該当します。
$Tile (a, b)$ はすべて the hat と同じタイリングができるわけですから、非周期的にタイリングが可能です。

ここで注意が必要なのは、 $Tile (a, b)$ の中には周期的にタイリングが可能なものが含まれているということです。

$a = 0$ のタイル、 $b = 0$ のタイル、 $a = b$ のタイルについては周期的なタイリングも可能なタイルとなっています。

上図でいうと、 $Tile (0, 1), Tile (1, 1), Tile (1, 0)$ の $3$ つが、周期的なタイリングも可能なタイルです。

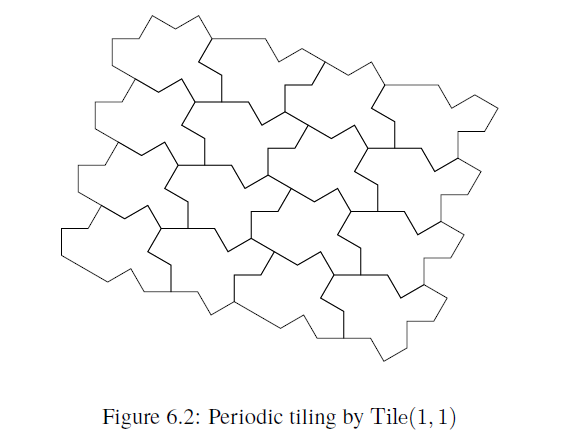論文より引用：Tile(1,1) は周期的なタイリングも可能

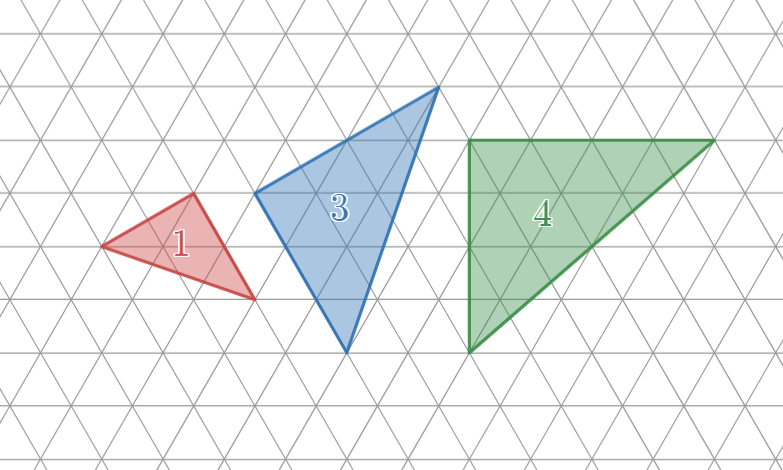
　また、 $Tile (0, 1)$ は正三角形４個、 $Tile (1, 0)$ は正三角形８個をつないだ形となっていることを確認してください。

　なお、正三角形４個からなる形をテトリアモンド、正三角形８個からなる形をオクティアモンドとも言います。

テトリアモンド、オクティアモンドについて

　テトリアモンド、オクティアモンドという言い方は、正三角形２個からなるひし形を「ダイアモンド」として、この「ダイ」の部分が2を表すものとみなして作られた造語です。このように正三角形を複数個つないだ形をまとめて「ポリイアモンド」とも言います。

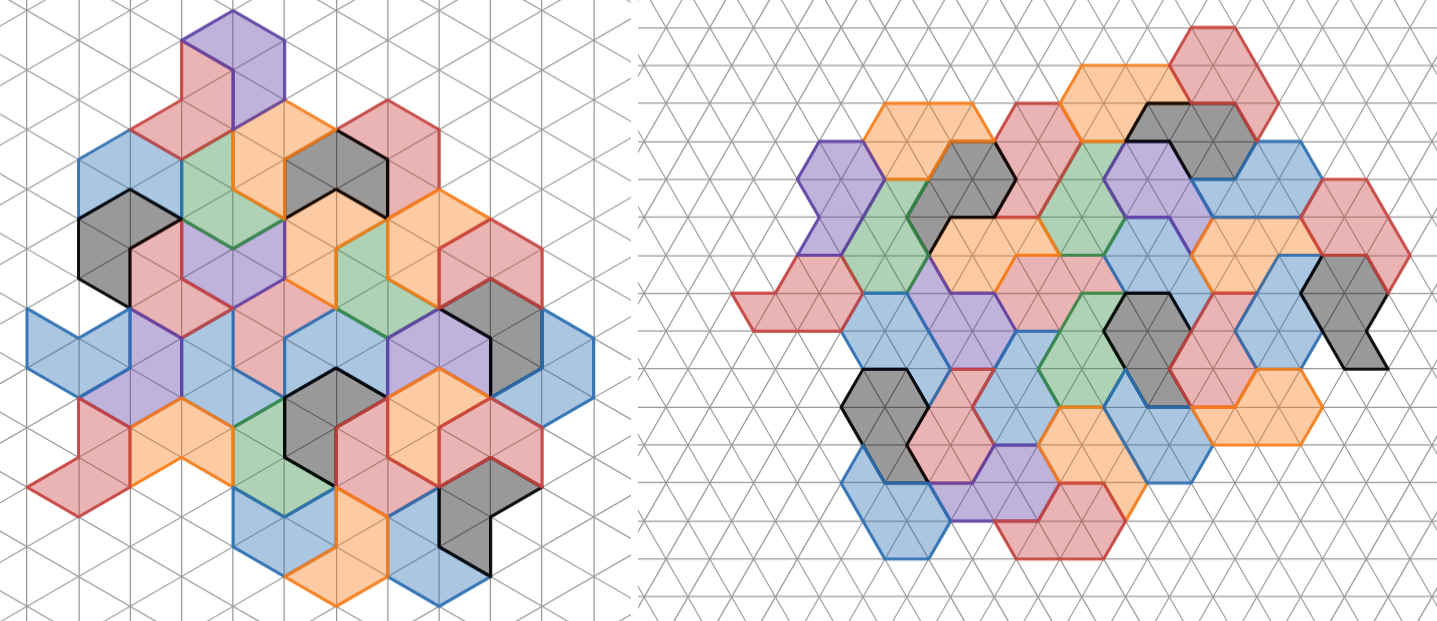Tile(0,1) と Tile(1,0) の対応する配置

　Tile(0,1) と Tile(1,0) はどちらも正三角形格子上に配置することができます。この時、オクティアモンドによる配置は、対応するテトリアモンドの配置の２倍の数の三角形を使っていますね。この事実は証明で使います。

§2§　正三角形格子の性質

　証明には、正三角形格子の格子点間の距離についてのある性質を使います。
　まず、正三角形格子の格子点間の距離の２乗がすべて整数になることを図から確認しましょう。（図は原点からの距離の2乗ですが、これが整数であることから格子点間の距離の2乗も整数であるとわかります）

正三角形格子の原点からの距離の２乗
　
　さらに、「正三角形格子の格子点の原点からの距離の２乗」が偶数になるとき、その素因数のうち2は必ず偶数個含まれるという性質があります。
　
　距離の２乗として現れる数を表にしましたので確認してみてください。

距離の２乗	素因数2を分解
$1$	$= 1$
$3$	$= 3$
$4$	$= 2^{2}$
$7$	$= 7$
$9$	$= 9$
$12$	$= 2^{2} \times 3$
$13$	$= 13$
$16$	$= 2^{4}$
$21$	$= 21$
$25$	$= 25$
$27$	$= 27$
$28$	$= 2^{2} \times 7$
$31$	$= 31$

　この事実を数式で確認しましょう。

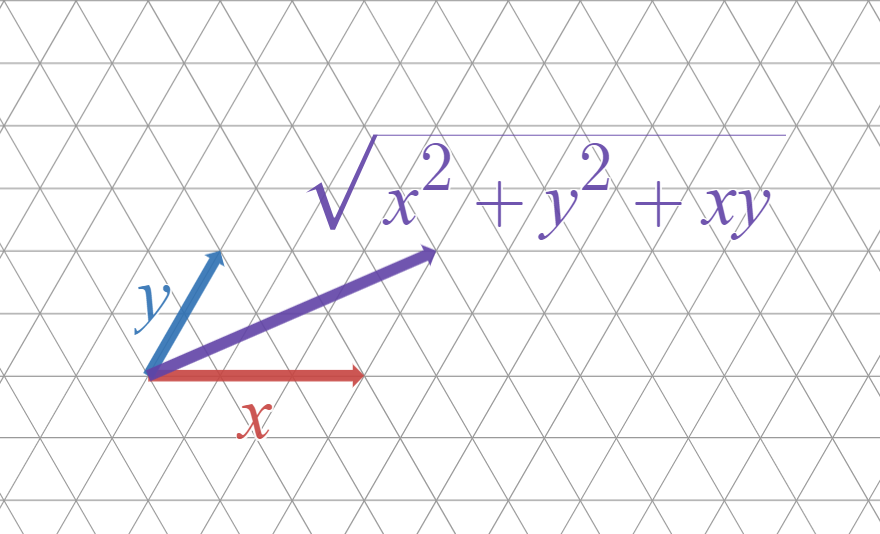格子点間の距離

　正三角形格子の格子点間の距離は、整数 $x, y$ を使って $\sqrt{x^{2} + y^{2} + x y}$ と表すことができることが、上図と余弦定理からわかります。

　したがって、正三角形格子の格子点間の距離の２乗は $x^{2} + y^{2} + x y$ と表すことができます。

$x, y$ がともに奇数のときは $x^{2} + y^{2} + x y$ は奇数
$x, y$ の片方が奇数、片方が偶数のときは $x^{2} + y^{2} + x y$ は奇数
$x, y$ がともに偶数のときは $x^{2} + y^{2} + x y$ は偶数

となることは、各項の偶奇を考えればすぐにわかりますね。
さらに、 $x, y$ がともに偶数のときについて、もう少し詳しく調べてみましょう。

$x, y$ がともに偶数のときは、 $k, l$ を奇数とし、 $m, n$ を自然数として、

$x = 2^{m} k$
$y = 2^{n} l$

と表すことができます。

$x^{2} + y^{2} + x y$ に代入すると、

$\begin{aligned} x^{2} + y^{2} + x y & = 2^{2 m} k^{2} + 2^{2 n} l^{2} + 2^{m + n} k l \end{aligned}$

となります。

$m$ と $n$ の大小で場合分けします。

(i) $m = n$ のときは、

$\begin{aligned} 2^{2 m} k^{2} + 2^{2 n} l^{2} + 2^{m + n} k l & = 2^{2 m} k^{2} + 2^{2 m} l^{2} + 2^{2 m} k l \\ = 2^{2 m} \underset{奇数}{\underset{⏟}{(k^{2} + l^{2} + k l)}} \end{aligned}$

(ii) $m > n$ のときは、

$\begin{aligned} 2^{2 m} k^{2} + 2^{2 n} l^{2} + 2^{m + n} k l & = 2^{2 n} \underset{奇数}{\underset{⏟}{(2^{2 (m - n)} k^{2} + l^{2} + 2^{m - n} k l)}} \end{aligned}$

(iii) $m < n$ のときは、

$\begin{aligned} 2^{2 m} k^{2} + 2^{2 n} l^{2} + 2^{m + n} k l & = 2^{2 m} \underset{奇数}{\underset{⏟}{(k^{2} + 2^{2 (n - m)} l^{2} + 2^{n - m} k l)}} \end{aligned}$

ですから、「 $x, y$ がともに偶数のときは $x^{2} + y^{2} + x y$ の素因数のうち2は必ず偶数個含まれる」ことになります。
したがって、このように書き直すことができます。

$x, y$ がともに奇数のときは $x^{2} + y^{2} + x y$ は奇数
$x, y$ の片方が奇数、片方が偶数のときは $x^{2} + y^{2} + x y$ は奇数
$x, y$ がともに偶数のときは $x^{2} + y^{2} + x y$ は素因数として2を必ず偶数個含む

まとめると、「正三角形格子の格子点間の距離の２乗は必ず整数になる。その整数の素因数のうち2は偶数個になる」ということになります。

正三角形格子の格子点間の距離の２乗の性質

正三角形格子の格子点間の距離の２乗は必ず整数になる。その整数の素因数のうち2は必ず偶数個になる。

相似な図形の面積比は、相似比の $2$ 乗になりますね。
また、「素因数のうち $2$ が偶数個」の数どおしの組で、「ちょうど $2$ 倍の数となるような組合せ」はありえませんね。

このことから、さらに次のことが言えます。

正三角形格子上の相似な図形の性質

正三角形格子の格子点をつないで相似な図形を作るとき、その図形の面積比は $2$ 倍となることはない。

正三角形格子上の相似な図形の面積比は2倍になることはない

§3§　証明の方針

　これで証明の準備ができました!
　ここからいよいよ証明に入ってきます。
　証明することは次のことです。

the hat により平面全体をタイリングしたとき、そのタイリングが「周期的なタイリング」になることはない。

　ここで「周期的」という言葉の意味は、タイリングに２方向以上の並進対称性があることを言います。
　「並進対称性」というのは、平行移動で元のタイリングと重ねることができる性質のことをいいます。
　
　実は、the hat には「1方向のみの並進対称性」もありませんし、そのことを証明することもできるのですが、それはこの記事のおまけとして最後に付け加えることにして、ここでは２方向以上の並進対称性をもつタイリングのことを「周期的なタイリング」と呼び、the hat が周期的なタイリングが不可能であることを証明します。

　証明には背理法を使います。
　the hat により「周期的なタイリング」ができると仮定して矛盾を導きます。　

§4§　証明の核心

仮定

　さて、ここからはthe hat により「周期的なタイリング」ができると仮定し、そのタイリングを $T$ で表すことにします。

(仮定)
the hat により「周期的なタイリング」ができると仮定し、そのタイリングを $T$ で表す。

先に書いたように、the hat のタイリングは、辺の長さを $2$ つの変数として変化させることで連続的に変形することができます。

(再掲)辺の長さを変化させてもタイリングできる

$T$ を同じ方法で変形させてできる、テトリアモンドのタイリングを $T_{4}$ 、オクティアモンドのタイリングを $T_{8}$ と呼ぶことにします。

(論文より引用)!FORMULA[93][2068380484][0] (論文より引用) $T, T_{4}, T_{8}$

タイリング $T$ 、 $T_{4}$ 及び $T_{8}$ は、タイルの隣接関係が保存されていますので、 $T$ が周期的なタイリングであれば、 $T_{4}$ も $T_{8}$ も周期的なタイリングとなるはずです。

　(2023.7.1追記)
　なぜ「 $T$ が周期的なタイリングであれば、 $T_{4}$ も $T_{8}$ も周期的なタイリングとなるはず」といえるのか、もう少し詳しく説明します。
　仮定より、 $T$ には $2$ 方向以上の並進対称性がありますので、タイリングの単位領域となる平行四辺形状の領域があるはずです。
　
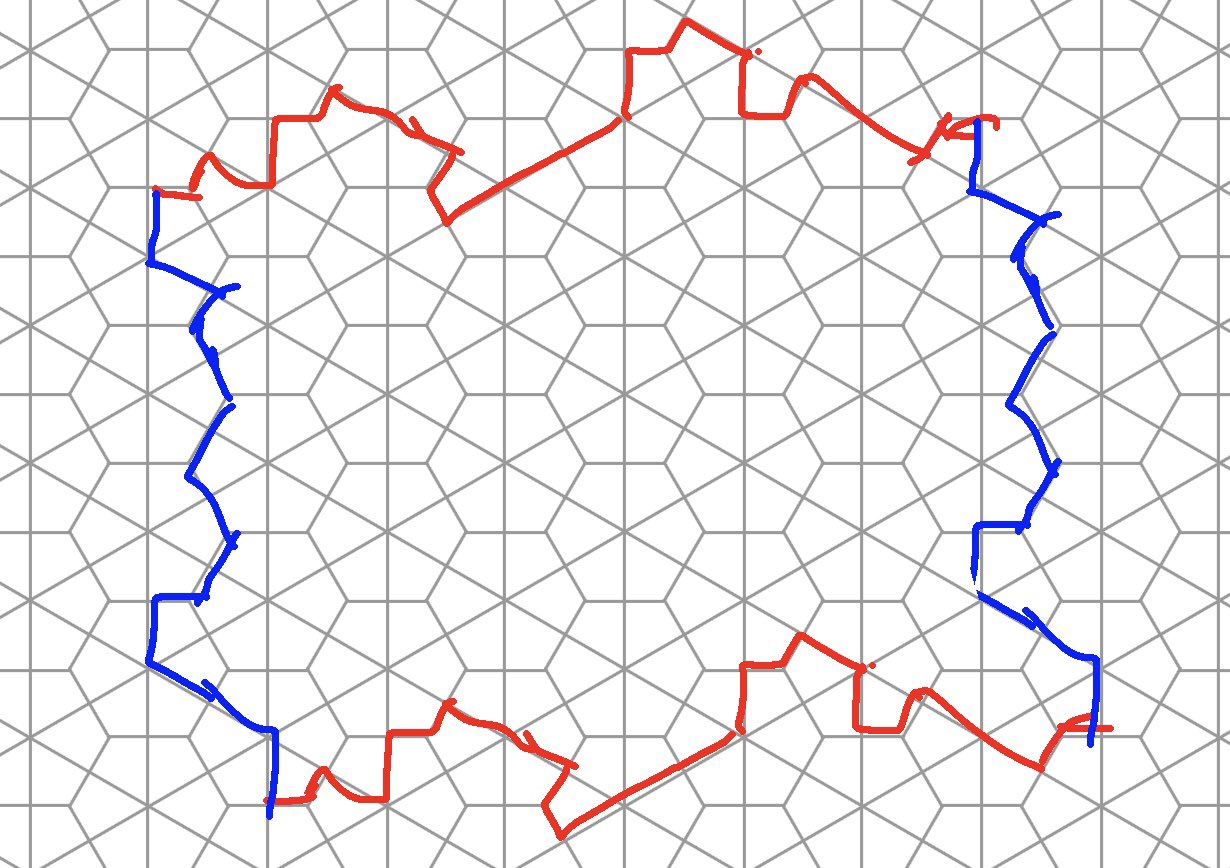　平行四辺形状の単位領域

　上下の赤い折れ線、左右の青い折れ線は合同です。
　単位領域の端は個々のタイルの辺と重なります。
　ここから連続的に変形させると、赤い折れ線と青い折れ線は必ず同じ形に変形します。
　したがって、 $T_{4}$ や $T_{8}$ に変形したとき、 $T$ の単位領域はそのまま $T_{4}$ や $T_{8}$ の単位領域となります。

相似にはならない

ここで、 $T_{4}$ の周期に対応する並進ベクトルを考え、それらに対応する $T_{8}$ の並進ベクトルを考えます。

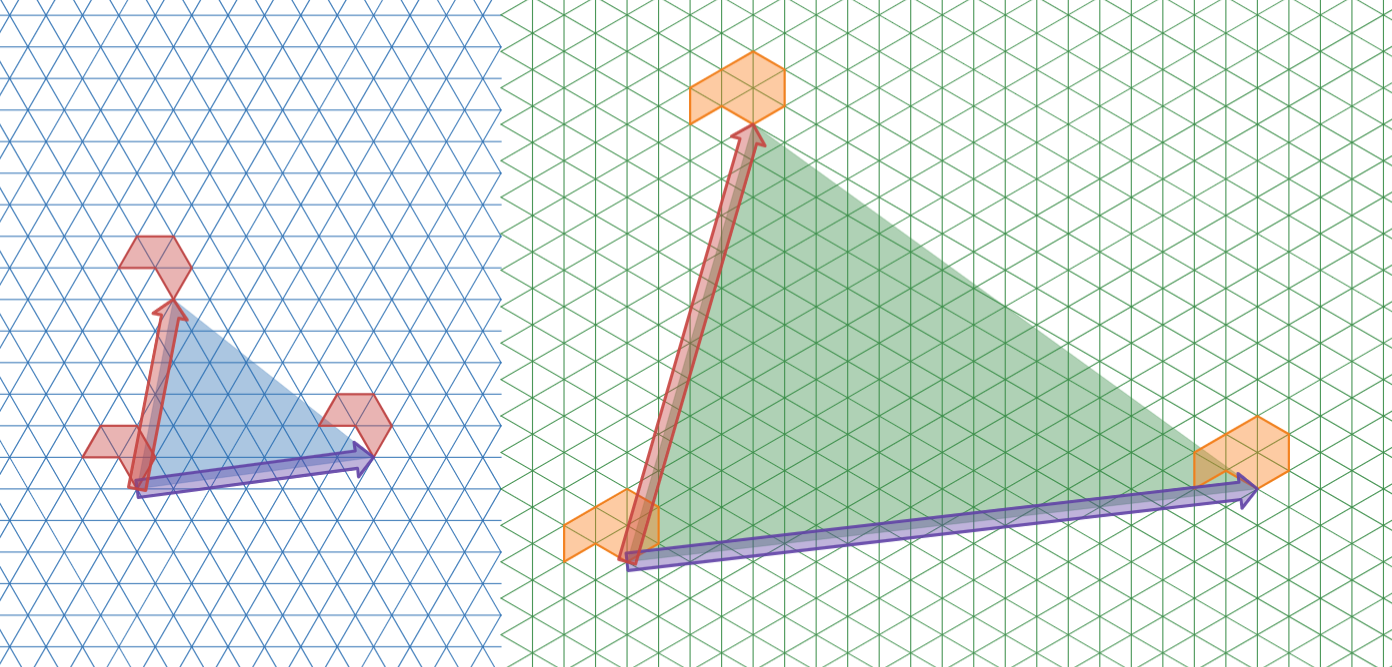対応する並進ベクトルを考える

このとき、タイルの数と単位三角形の枚数の関係について、 $T_{4}$ はタイル $1$ 枚あたり $4$ 個、 $T_{8}$ はタイル $1$ 枚当たり $8$ 個の単位三角形を使うことになりますが、定理 $2$ で示したとおり、「正三角形格子の格子点をつないで相似な図形を作るとき、その図形の面積比は $2$ 倍となることはない」のですから、 $T_{4}$ の周期に対応する並進ベクトルからなる三角形と、それらに対応する $T_{8}$ の並進ベクトルからなる三角形は相似にはならないはずです。

相似になる

さて、次に、 $T_{4}$ の周期に対応する並進ベクトルからなる三角形と、それらに対応する $T_{8}$ の並進ベクトルからなる三角形で相似になるものがあることを示して、背理法を完成させましょう。

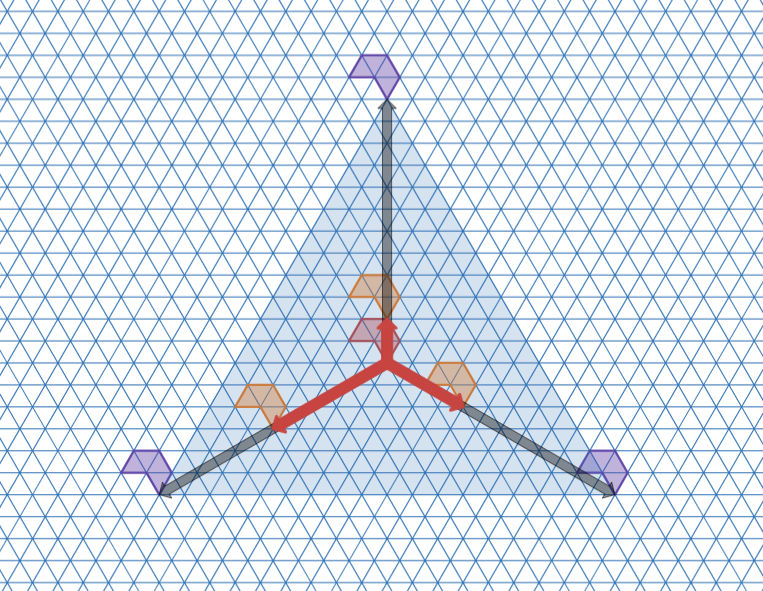
そのために、まず、「 $T_{4}$ の周期に対応する $3$ 方向のベクトルで、互いに120度の向きで同じ大きさのものを構成できる」ことを示します。

　それには、「ある周期の倍数もまた周期となる」という事実を使えばよいです。

　 $T_{4}$ の中からテトリアモンドを１つ選び、そこから120度ずつ3方向に探索していくと、 $T_{4}$ は仮定より周期的なタイリングなので、どの方向でも必ずどこかでループします。各方向の周期を調べ、見つかった周期の最小公倍数を新たな周期とすれば、「 $T_{4}$ の周期に対応する $3$ 方向のベクトルで、互いに120度の向きで同じ大きさのもの」が構成できますね。

　それらを使えば、「並進ベクトルからなる正三角形」をつくることができます。

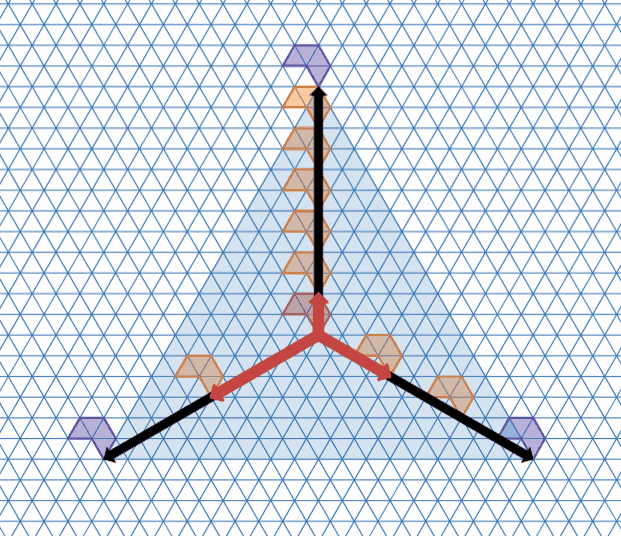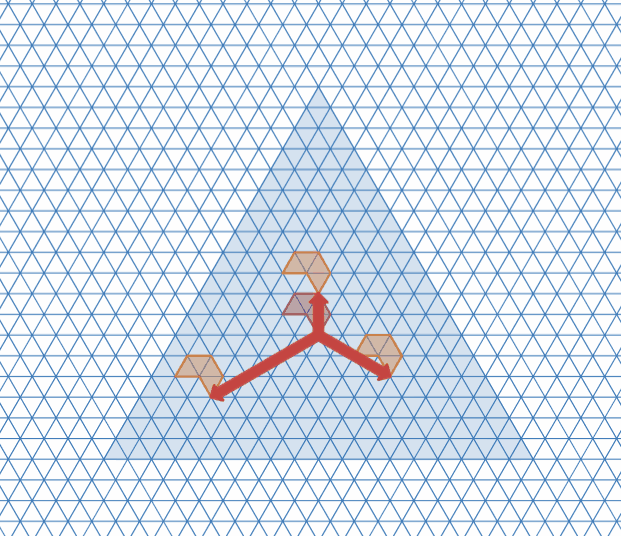最小公倍数を使って並進ベクトルで正三角形を作る

　次に、この $T_{4}$ 上の「並進ベクトルからなる正三角形」に対応する $T_{8}$ 上の「並進ベクトルからなる三角形」を考えます。もし、その三角形が正三角形であるといえれば、正三角形格子の格子点を繋いだ相似な図形で面積比が2倍の組が存在することになり矛盾。背理法を完成させることができます。

　というわけで、ここからは、次のことを証明することが目標になります。

背理法を完成させるために証明するべきこと

$T_{4}$ 上の「並進ベクトルからなる正三角形」に対応する $T_{8}$ 上の「並進ベクトルからなる三角形」は正三角形である

矛盾、そして背理法の完成

　ここまでで、「後もう少しで証明できそう」と思いましたか?
　残念ながら、ここからが長いのです・・・が順番に説明しますのでご安心ください。

　まず、 $T_{4}$ の各タイルの辺がが次のようなひし形格子の辺と重ねられることを確認してください。
　
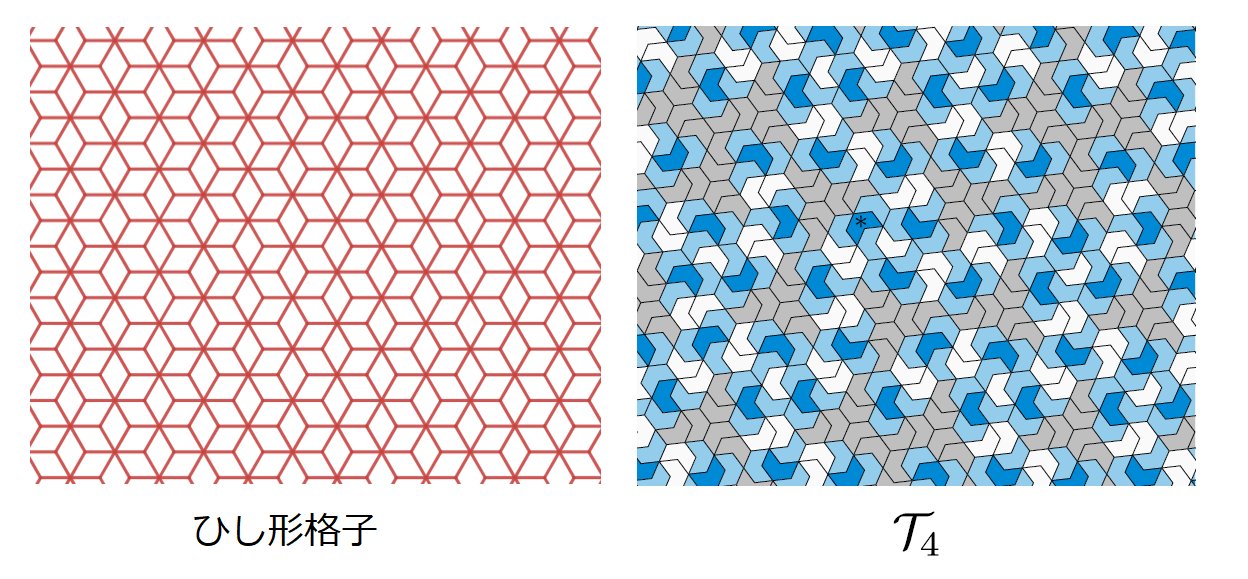ひし形格子との関係。右画像は論文より引用

　テトリアモンドを自由にタイリングした場合にはひし形格子と重ならない配置もあるのですが、 $T_{4}$ の場合はテトリアモンド同士がひし形格子と重なる向きにしか隣接しないため、必ずひし形格子と重なる配置になっています。

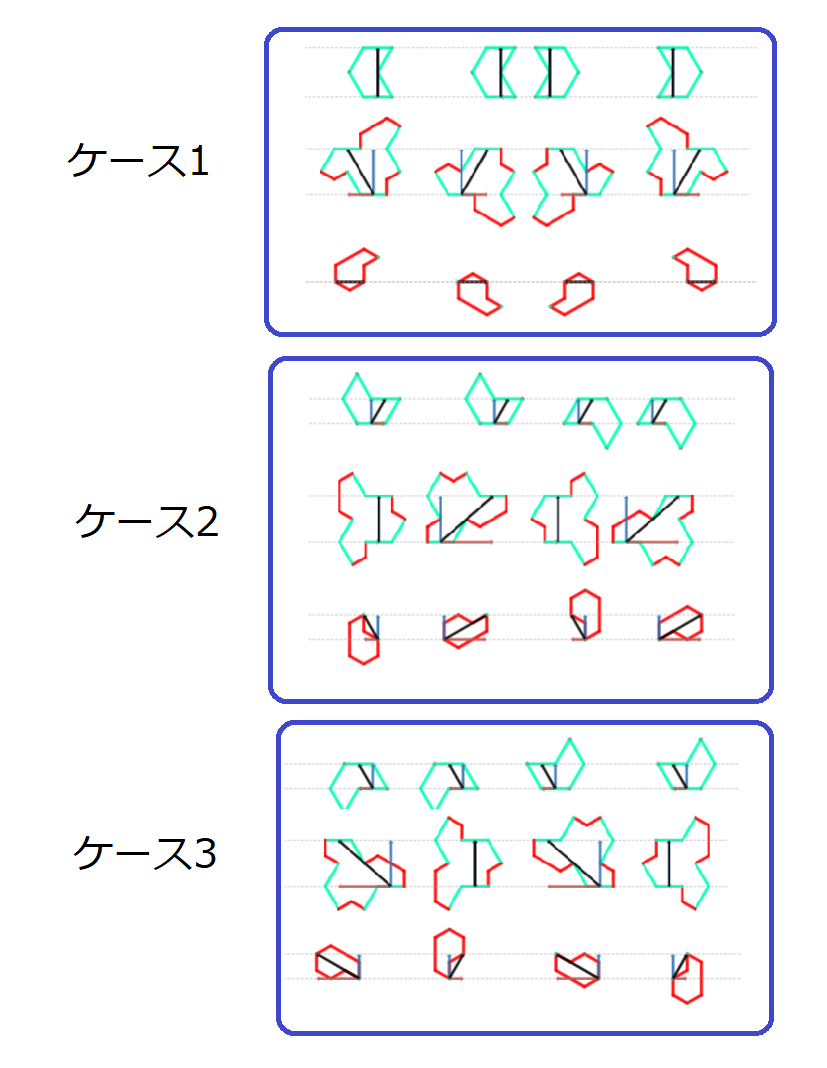
　ひし形の向きは $3$ 種類あります。ひし形格子には $3$ つの向きが均等にありますので、タイリングの単位領域内にはそれぞれの向きが同じ数ずつあるはずです。

　テトリアモンドを $2$ つのひし形に分割すると、 $3$ つの向きのうち $2$ つが含まれていて、残る $1$ つの向きは含まれていません。
　テトリアモンドは $6$ つの向きがありますが、含まれているひし形の向きで $3$ 種類にわけ、ケース $1$ ～ケース $3$ と呼ぶことにします。

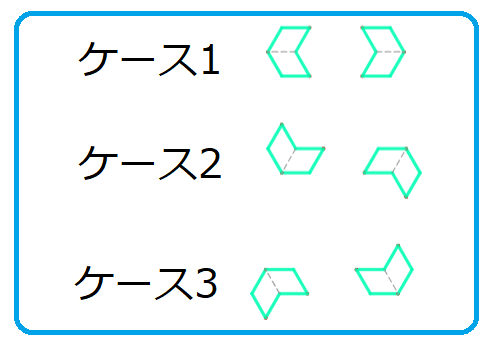ケース1～ケース3

　タイリングの単位領域内には、ひし形の各方向が均等に含まれているのですから、ケース $1$ ～ケース $3$ は単位領域内に同じ数ずつ含まれているはずです。

単位領域内の各ケースの割合

ケース $1$ ～ケース $3$ は単位領域内に同じ数ずつ含まれている

　次に、タイリングの単位領域を図のように長方形状にとり、ベルト状の領域に分割します。

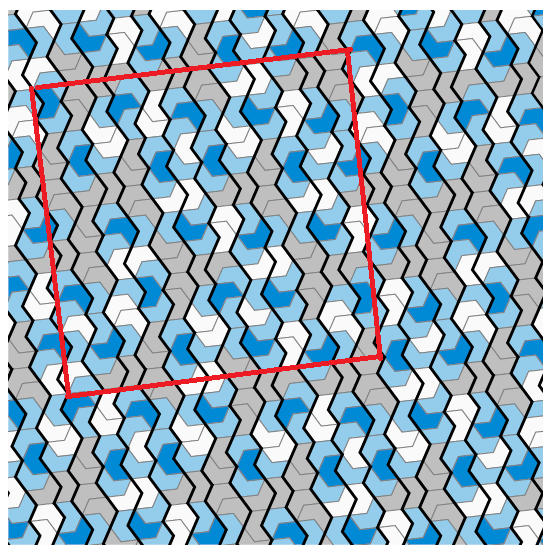長方形上の単位領域(画像は論文のものを加工)

　画像中の赤い長方形が周期的なタイリングの単位領域になっていると思ってください。(背理法のために、「周期的にタイリングしたもの」と仮定していることを思い出してください。)

　上の画像で、単位領域内を黒い線でベルト状に分割していることも確認してください。

　ベルト状の領域は、つぎのように構成することで一意に定まります。

ベルト状の領域の構成方法(画像は論文から引用)

　まず、上の図の、 $T_{4}^{'}$ のように、ひし形タイリングの方向を $1$ つ選び、その方向のひし形の辺を太線にすると、残る $2$ つの方向のひし形タイルがベルト状につながります。

それから、太線で囲まれたひし形を、それぞれ、 $T_{4}$ の対応するテトリアモンドの属するベルト状の領域に合体させます。

　これで、 $T_{4}$ の領域をベルト状に一意に分割することができました。このベルト状の領域を、論文にならって、「i-strip」と呼ぶことにします。

　さて、タイリングの単位領域内には、ケース $1$ ～ケース $3$ のテトリアモンドが $\frac{1}{3}$ ずつ含まれていることは先に書いた通りですが、i-strip 内のテトリアモンドの割合についても似たような性質があります。

(各i-strip のケース $1$ のタイルの割合)

　それぞれの i-strip 内で、ケース $1$ のテトリアモンドの数は全体の $\frac{1}{3}$ となる。
　ただし、i-stripの向きと直交する向きをケース $1$ として考える。

　ここで「テトリアモンドの向き」は、テトリアモンドを矢印に見立てたときの向きと考えてください。それが、i-stripの向きと直角なものをケース $1$ にするということです。
　言い換えると、先ほどの $T_{4}^{'}$ のベルト状の領域内にテトリアモンド全体が含まれる向きをケース $1$ にするということです。

そのことをこれから示します。

　i-strip内のテトリアモンドもまた周期的になるので、その周期に対応する並進ベクトルを考え、さらに、そのベクトルに対応する $T_{8}$ のベクトルがどのようになるか考えます。

!FORMULA[166][-691552839][0] と !FORMULA[167][-691552715][0] の対応する並進ベクトルの関係 $T_{4}$ と $T_{8}$ の対応する並進ベクトルの関係

　各i-strip内のテトリアモンドについて、i-stripの向きと直交する向きの辺の中点をつなぐベクトルを考えます。

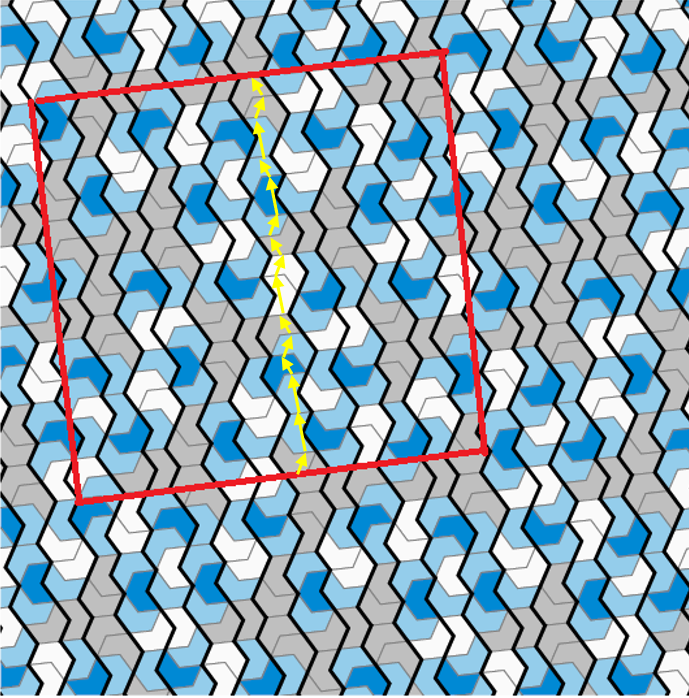テトリアモンドの辺の中点をつなぐベクトル

　つまり、i-stripの並進ベクトルを個々のテトリアモンドのベクトルの和と考えます。

　次に、 $T_{4}$ から $T_{8}$ へ連続的に変化させたときの個々のテトリアモンドのベクトルの変化を考え、その変化の和として、 $T_{8}$ 上の対応する領域の並進ベクトルを考えます。

　ケース $1$ ～ケース $3$ のそれぞれに対応するオクティアモンドは $4$ つずつありますので、それぞれの対応するベクトルを観察してみましょう。

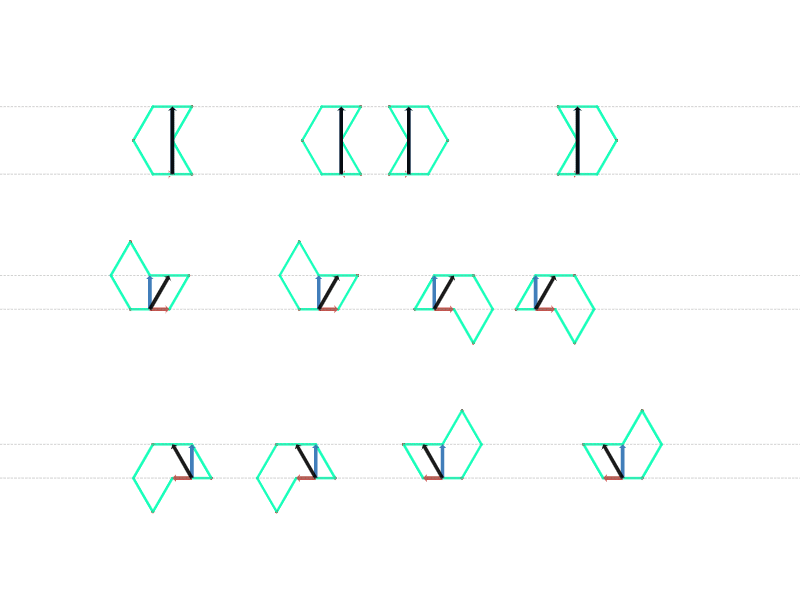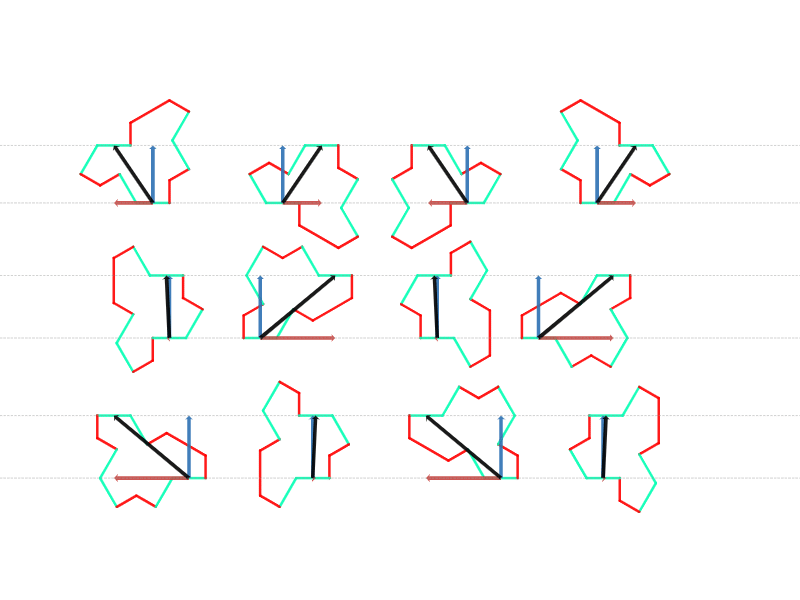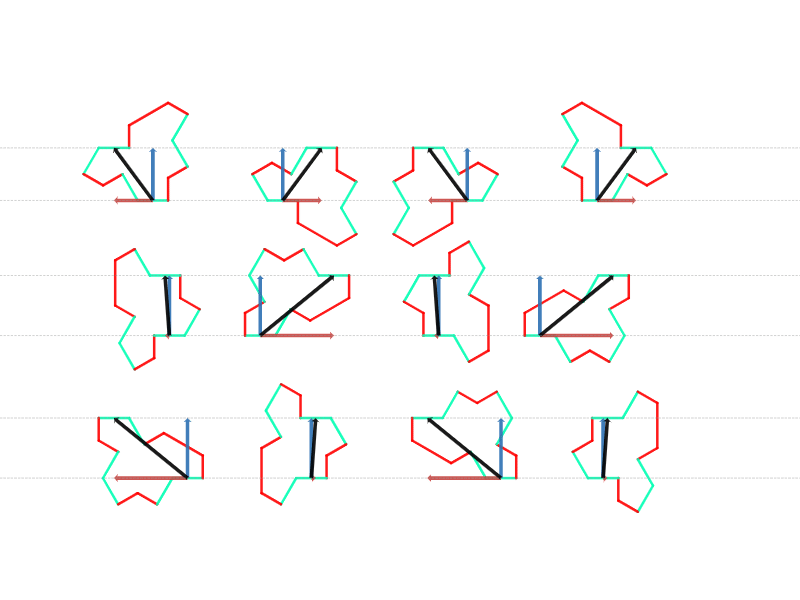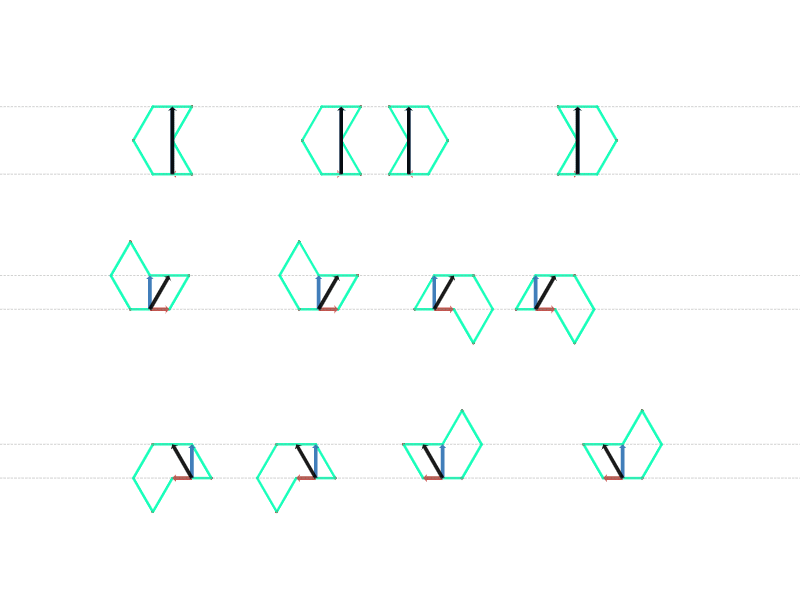対応するオクティアモンドのベクトル(GIF)

対応するオクティアモンドのベクトル

　すると、図のように、対応するベクトルの垂直成分については同じケースのものは同じになっていることがわかります。水平成分についてはバラバラですが、ここでは気にしなくてもかまいません。
　
　もう少し具体的に言うと、ケース $1$ の場合は垂直方向の成分ゼロ、ケース $2$ 又は $3$ の場合は垂直方向の成分は変化しないことがわかります。

　ところで、 $T_{4}$ と $T_{8}$ のタイルの隣接関係は保存されていますので、 $T_{4}$ の単位領域に対応する $T_{8}$ の領域もまた周期的になるはずです。
　したがって、i-strip の並進ベクトルに対応する $T_{8}$ のベクトルもまた周期的になり、かつ、それらのベクトルはすべて一致するはずです。
　そうすると、各i-stripの単位領域内にあるテトリアモンドのうちケース $1$ のテトリアモンドの割合は、どのi-strip でも同じになるはずであり、その割合はすべて $\frac{1}{3}$ になるはずということになります。

各i-strip のケース

1

のタイルの割合

　では、ここからは数式を使いましょう。

!FORMULA[188][-376030215][0] $L_{i}, v_{i}, v_{i}^{'}$

　 $T_{4}$ (と $T_{4}^{'}$ ) と重なる正三角形格子は、 $3$ 方向の平行線の組からできています。これらの平行線の組を、 $L_{1}, L_{2},$ 及び $L_{3}$ と呼びます。
各 $L_{i}$ の $2$ 本の連続する直線の間にあり、それらの直線に直交するベクトルを $v_{i}$ とします。ただし、異なる $v_{i}$ のなす角度が $120$ 度となるように向きを選びます。(図 $24$ を見てください。)

$v_{i}$ に直交し、 $v_{i}$ の $1 / \sqrt{3}$ の長さのベクトルを $v_{i}^{'}$ とします。ここでも、異なる $v_{i}^{'}$ のなす角度がすべて $120$ 度となるように選びます。

　先にも書いたように、最小公倍数を使って $T_{4}$ の並進ベクトルで正三角形を作ることができます。(図25参照)

並進ベクトルで作る正三角形

　正三角形となる並進ベクトルを、 $a v_{i}$ と表すことにします。
　
　明らかに、 $\sum_{i} a v_{i} = 0$ です。
　
　 $T_{4}$ から $T_{8}$ に連続的に変形したときに、 $a v_{i}$ がどのように変化するか考えます。

　 $a v_{i}$ をテトリアモンド単位に分割すると、ケース $1$ のテトリアモンドの数は全体の $\frac{1}{3}$ となります。

　ケース $1$ のテトリアモンドの $v_{i}$ 方向の成分はゼロに、ケース $2, 3$ のテトリアモンドの $v_{i}$ 方向の成分の大きさは変化しないことから、 $T_{4}$ 上の $a v_{i}$ に対応する $T_{8}$ のベクトルは $\frac{a}{2} v_{i} + b_{i} v_{i}^{'}$ のように書くことができます。

　ところで、 $T_{4}$ から $T_{8}$ に連続的に変形したときの、 $a v_{i}$ の変化はアフィン変換であり、アフィン変換では、和がゼロになるベクトルは和がゼロのままですから、

　 $\sum_{i} (\frac{a}{2} v_{i} + b_{i} v_{i}^{'}) = 0$

となります。まとめると、

$\sum_{i} a v_{i} = 0$
$\sum_{i} (\frac{a}{2} v_{i} + b_{i} v_{i}^{'}) = 0$

第 $1$ 式を使って第 $2$ 式から $v_{i}$ を消去することで

$\sum_{i} b_{i} v_{i}^{'} = 0$

が得られます。

　 $\sum_{i} b_{i} v_{i}^{'} = 0$ は、すべての $b_{i}$ が等しい場合のみ成り立ちます。

　そうすると、 $T_{8}$ の3つの並進ベクトル（ $\frac{a}{2} v_{i} + b v_{i}^{'}$ ）は互いに $120$ 度の角度をもつ同じ長さのベクトルとなります。

これは、 $T_{4}$ 上の「並進ベクトルからなる正三角形」に対応する $T_{8}$ 上の「並進ベクトルからなる三角形」が正三角形であることを意味します。

$T_{4}$ 上の「並進ベクトルからなる正三角形」に対応する $T_{8}$ 上の「並進ベクトルからなる三角形」は正三角形である

　"the hat" で周期的なタイリング𝓣ができる」と仮定したことにより矛盾が起きました。背理法により、"the hat" により平面全体をタイリングしたときそのタイリングが「周期的なタイリング」になることはないことが証明できました!

the hat は非周期的にしかタイリングできない

the hat により平面全体をタイリングしたとき、そのタイリングが「周期的なタイリング」になることはない。

おまけ1　the hat には「1方向のみの並進対称性」もない

　最初の方にも書きましたが、the hat は $2$ 方向以上の並進対称性のタイリングを作ることができないだけではなく、「 $1$ 方向のみの並進対称性のタイリング」も作ることもできません。
　そのことを証明するためには、次のことを示せばよいです。

示すべきこと

the hat で $1$ 方向以上の並進対称性のタイリングを作ることが可能ならば、 $2$ 方向以上の並進対称性のタイリングを作ることも可能である。

　 $2$ 方向以上の並進対称性のタイリングを作ることが不可能であることは証明済なので、対偶により、 $1$ 方向以上の並進対称性のタイリングを作ることも不可能であることが証明できるというわけです。

　そして、「示すべきこと」を示すには次のようにすればよいです。

edge-path を考える

　上図の青色や黄色の折れ線は、タイリングに使ったタイルの辺を順につないだものです。edge-path と呼ぶことにします。

$2$ 本の青い edge-path は同じ形になっていますが、これは並進対称の１周期分ずれたものを表しています。

　赤い縦線が２本あります。その幅は、the hat の最大の幅の２倍分をとっています。

　黄色の edge-path は、赤い縦線の間を通るように任意に選びます。

　さて、赤い縦線の組を水平方向へ動かすことを想像してください。

　動かすにつれ、黄色の edge-path をそれにあわせて変化させます。

　黄色の edge-path の形状は様々に変化しますが、そのパターンは高々有限とおりなので、必ず同じ形状になる組合せが出てきます。その組み合わせと青い edge-path を使えば、長方形状の単位領域を作ることができます。

　長方形状の単位領域は、上下・左右に繰り返すことで、"2" 方向以上の並進対称性のタイリングを構成することができます。

　これこそが「示すべきこと」でした。

おまけ2　Spectre について

　the hat の衝撃がまだやまない $2023$ 年 $5$ 月 $28$ 日、界隈をさらなる衝撃が襲いました。
　the hat はタイリングの一部に鏡像(裏返し)のものも使う必要があったため、「鏡像を使わない非周期モノタイルは存在するか」は未解決のままだったのです。
　しかし、そのようなタイルが発見されたのです!そのタイルには "Spectre" と名付けられました。("Spectres" と書く場合もあります。)

論文: A chiral aperiodic monotile

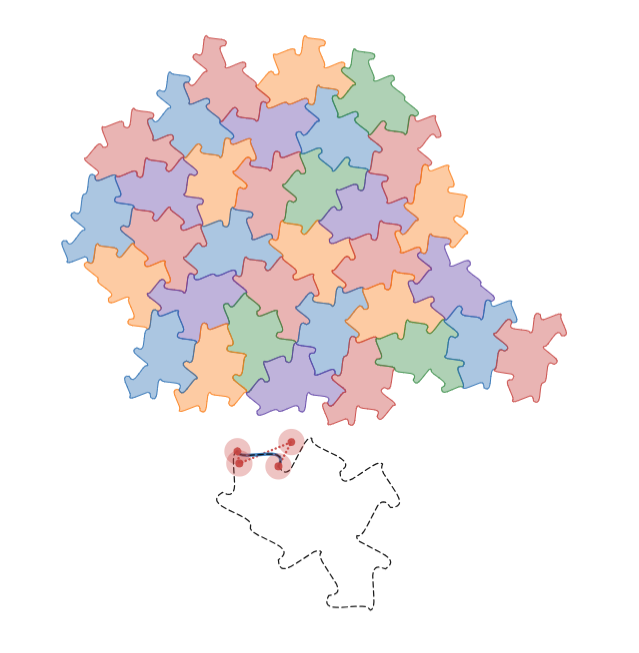Spectre Spectre

　この Specre ですが、実は　the hat の論文に出てくる $Tile (1, 1)$ と本質的に同じ形状です。
　ただし、鏡像を使ったタイリングができないように、辺を変形させたものです。
　鏡像を使えないように変形するだけで「鏡像を使わない非周期モノタイル」ができるとは、本当に驚きです。しかも、元になる $Tile (1, 1)$ は、非周期的にタイリングできる the hat の族でありながら例外的に周期的にもタイリングできる形状だったのですから・・・。

　となると、今回の記事で証明したのと同じ方法で Spectre の非周期性も証明できそうだと思いませんか?
　残念ながら、そううまくはいかないようです。Spectre も辺の長さを変数にして連続的に変形することで別のタイリングにすることが可能なのですが、その場合、必ず２種類のタイルを使うタイリングになってしまうため、今回の記事の手法は使えません。

・　連続的に変形させているツイート

The aperiodic Tile(a, b) can be constructed as a 4D skew nonplanar polygon then projected to 2D. Changing the projection direction, we can get the whole continuum including hat, turtle, and the non-curvy spectre. For some directions, we get a self crossing polygon in 2D. 1/2 pic.twitter.com/LN4muFNYtY
— Nan Ma (@mananself) June 9, 2023

　とはいえ、今回の記事のようなエレガントな証明方法があるかもしれませんので、エレガントな別証明を探してみるのも面白そうです。

おまけ3　論文を読んでみよう

　元の論文の内容はかなりボリュームがあり、私はまだ論文の全体を理解できたわけではありません。
　しかしながら、「周期的に敷き詰めることが不可能であること」の証明の核心部分は理解できたと思っています。

　もう少し詳しく言うと、論文では次のように $2$ とおりの方法で証明しているのですが、私が理解できたと思っているのはそのうち証明方法 $1$ のほうです。上記の記事の証明方法も、証明方法 $1$ を簡略化したものです。

【証明方法 $1$ 】
　　the hat を周期的にタイリングすることができたと仮定して矛盾を導く方法。(論文のセクション $3$ に掲載されています。)
　　
【証明方法 $2$ 】
　　the hat を平面全体に敷き詰めるためにはあるルールにしたがって配置しなければならないことから非周期性を示す方法。(論文のセクション $4$ ・ $5$ に掲載されています。)

　実際には証明方法 $2$ の方が先にできていたらしいのですが、論文では証明方法 $1$ を先にセクション $3$ に掲載しています。

　そのことから、私は「証明方法1の方が著者のオススメなのではないか」と思っています。(考えすぎかもしれません。)

　また、the hat が非周期的タイルであることを証明するためには、「周期的に平面を敷き詰めることが不可能である」ことだけではなく、「平面全体を敷き詰めることが可能である」ということも証明しなければいけません。

「the hat が周期的に平面を敷き詰めることが不可能である」
+
「the hat は平面全体を敷き詰めることができる」
=
「the hat は平面を非周期的に敷き詰めることができるが、周期的には敷き詰めることができない」

　このことについて、論文では、H・T・P・Fの4種類の構造を再帰的に組み合わせる方法でタイリングできることから証明しています。

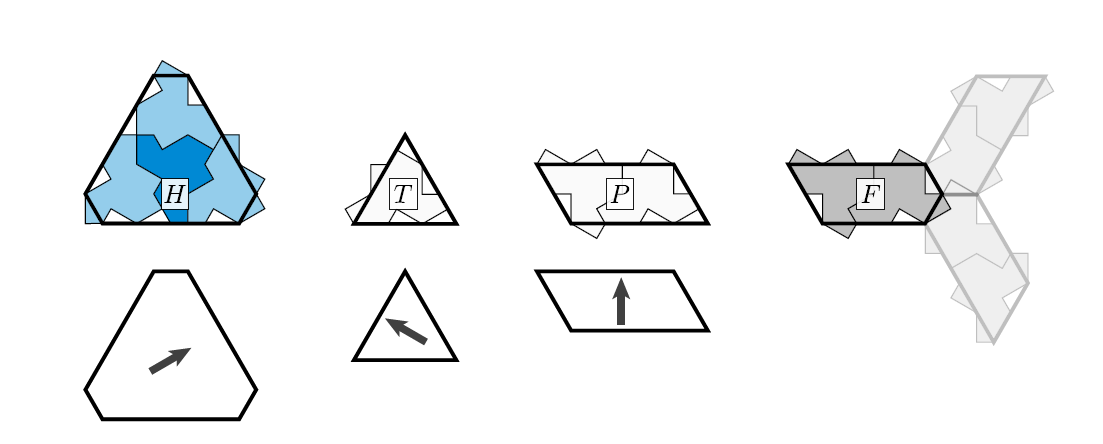論文より引用。H,T,P,F の４種類の構造

論文より引用。再帰的なタイリングの構造

論文中の専門用語

　論文にはたくさんの専門用語が出てきます。
　ここに簡単な説明をまとめましたので、わからない用語が出てきたら随時確認してください。

用語

・polyform「ポリフォーム」　……　特定の図形をつなぎあわせて作られた図形。テトリスのブロックもポリフォームの一種。
・polyamond「ポリイアモンド」　……　同じ大きさの正三角形を辺でつないだポリフォーム。ダイアモンドを正三角形二つつないだひし形ととらえて作られた造語。
・polykite「ポリカイト」　……　正六角形を辺の中点と中心を結ぶ線分で分割してできる形をカイト(凧型)と呼び、カイトをつないで作るポリフォームをポリカイトと呼ぶ。the hat もポリカイトの一種。

・weakly periodic「弱く周期的」……無限位数の対称群をもつタイリングのことを弱く周期的なタイリングと呼ぶ。
・strongly periodic「強く周期的」……その対称群が空間全体にココンパクト(cocompact)な作用を持つ離散部分群を持つようなタイリングを強く周期的なタイリングと呼ぶ。

※　平面上に合同なタイル(複数種類の場合を含む)を敷き詰めるタイリングに限定していえば、"weakly periodic"　は「 $1$ 方向以上の並進対称性を持つ」、"strongly periodic" は「 $2$ 方向以上の並進対称性を持つ」と解釈して問題なさそうです。

・weakly aperiodic「弱く非周期的」……タイルの集合（または単一のタイル）が弱く非周期的であるとは、タイリングは可能だが強く周期的なタイリングは不可能であることを意味する。
・strongly aperiodic「強く非周期的」……タイルの集合（または単一のタイル）が強く非周期的であるとは、タイリングは可能だが弱く周期的なタイリングは不可能であることを意味する。

・symmetric group「対称群」……置換（permutation）を元とする群。

・cocompact「ココンパクト」……群論において「離散部分群の商空間がコンパクトである」という性質を持つものを指す。

・Laves tiling[3.4.6.4] ……　カイトを敷き詰めてできるタイリング。頂点回りを３等分・４等分・６等分・４等分するように辺が配置される。Archimedean tiling(3.4.6.4) (正三角形、正方形、正六角形、正方形が頂点の周りに並ぶようなタイリング)と双対の関係にある。the hat はこのタイリングの上に、辺が重なるように整列させて(aligned)タイリングすることができる。

Laves tiling[3.4.6.4]